Знание максимальной цифры в числе может быть полезно во многих ситуациях. Независимо от того, занимаетесь ли вы программированием, математикой или просто любите головоломки, вы будете рады узнать эффективные методы и советы для определения максимальной цифры в числе.
Один из самых простых способов найти максимальную цифру в числе – это использовать цикл. Мы можем пройти по каждой цифре числа, сравнивая их друг с другом и запоминая наибольшую. При этом помните, что важно использовать правильное условие выхода из цикла, чтобы не получить ошибку.
Если вам интересно повысить эффективность своего алгоритма, вы можете использовать способ, основанный на разложении числа на цифры. Это можно сделать, например, с помощью операции деления на 10 и остатка от деления. Обработка каждой цифры будет производиться отдельно, что позволяет легко определить максимальную цифру.
Не забывайте также о работе с числами, представленными в виде строк. В этом случае, чтобы найти максимальную цифру, можно использовать методы работы со строками, такие как поиск наибольшего символа или сортировка. Независимо от выбранного метода, помните о важности проверки входных данных и выборе наиболее подходящего решения для вашей конкретной задачи.
Как найти максимальную цифру в числе: полезные методы и советы

При работе с числами часто возникает задача найти наибольшую цифру в числе. Эта задача может быть полезна для решения различных задач, например, при поиске максимального значения в массиве чисел или при анализе данных.
Существует несколько различных методов, которые могут помочь в решении этой задачи. Рассмотрим некоторые из них:
- Использование цикла и операции получения остатка от деления на 10.
- Преобразование числа в строку и работа с символами.
1. Использование цикла и операции получения остатка от деления на 10. Данный метод заключается в следующем:
1.1 Инициализируем переменную maxDigit значением 0.
1.2 Используем цикл, в котором на каждой итерации получаем остаток от деления числа на 10.
1.3 Если текущий остаток больше значения переменной maxDigit, обновляем значение maxDigit.
1.4 Делим число на 10 и повторяем шаги с 1.2 до 1.4, пока число не станет равным 0.
1.5 В конце работы цикла значение переменной maxDigit будет содержать максимальную цифру в числе.
2. Преобразование числа в строку и работа с символами:
2.1 Преобразуем число в строку.
2.2 Используем цикл для перебора символов в строке.
2.3 Преобразуем каждый символ обратно в число и сравниваем его с текущим максимальным значением.
2.4 Если текущий символ больше значения переменной maxDigit, обновляем значение maxDigit.
2.5 Повторяем шаги с 2.2 до 2.4 для всех символов в строке.
2.6 В конце работы цикла значение переменной maxDigit будет содержать максимальную цифру в числе.
Выбор конкретного метода зависит от конкретной задачи и предпочтений программиста.
Теперь вы знаете полезные методы и советы, которые помогут вам найти максимальную цифру в числе. Используйте их в своей работе для решения различных задач.
Простой перебор

Для начала объявим переменную maxDigit, которая будет хранить текущую максимальную цифру. Предположим, что максимальная цифра - это первая цифра числа. Затем, используя цикл, мы сравним каждую следующую цифру числа с текущей максимальной и, если она больше, обновим значение переменной maxDigit.
Ниже приведен пример кода на языке JavaScript, демонстрирующий этот подход:
let number = 987654321; // заданное число
let maxDigit = number % 10; // предположим, что первая цифра - это максимальная
number = Math.floor(number / 10); // убираем первую цифру
while (number > 0) {
let digit = number % 10; // получаем текущую цифру
number = Math.floor(number / 10); // убираем текущую цифру
if (digit > maxDigit) {
maxDigit = digit; // обновляем максимальную цифру
}
}
Преимущество такого подхода заключается в его простоте и эффективности. Он позволяет найти максимальную цифру в числе без использования сложных математических операций или регулярных выражений. Однако стоит учесть, что он не является самым оптимальным способом в случае больших чисел или множественных операций поиска максимальной цифры.
Разложение на цифры
Для нахождения максимальной цифры в числе необходимо сначала разложить число на отдельные цифры. Это можно сделать с использованием различных методов:
- Метод деления по модулю: число последовательно делится на 10, пока оно больше 0. В каждой итерации получаем последнюю цифру числа с помощью операции остатка от деления на 10.
- Преобразование числа в строку: число преобразуется в строку и затем каждый символ строки преобразуется обратно в число.
- Использование рекурсии: число содержит знаки и цифры, которые можно извлечь, пока они не исчезнут.
После разложения на цифры можно сравнить каждую цифру с предыдущей максимальной и, если она оказывается больше, обновить значение максимальной цифры.
Знание этих методов поможет вам эффективно находить максимальную цифру в числе.
Использование встроенных функций

Для определения максимальной цифры в числе в языке программирования можно использовать встроенные функции.
Одна из таких функций - это функция, возвращающая наибольшую цифру в числе. Для этого можно воспользоваться функцией max(), которая принимает неограниченное количество аргументов и возвращает наибольший из них.
Пример использования функции max() для нахождения максимальной цифры в числе:
```python
number = 12345
max_digit = max(str(number))
Такой подход позволяет с легкостью находить максимальную цифру в числе без необходимости использования сложных алгоритмов или циклов. Встроенные функции могут существенно упростить процесс обработки чисел и повысить его эффективность.
Применение алгоритма поиска максимального значения
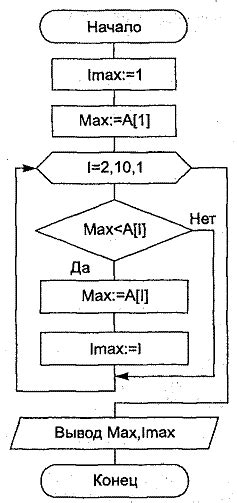
Алгоритм поиска максимального значения можно разделить на несколько шагов:
- Преобразование числа в строку с помощью метода
str(). - Инициализация переменной для хранения максимального значения.
- Обход всех символов строки с помощью цикла
for. - Преобразование текущего символа обратно в число с помощью метода
int(). - Сравнение текущего значения с максимальным значением. Если текущее значение больше максимального, то оно становится новым максимальным значением.
После завершения обхода всех символов получаем максимальное значение, которое можно использовать для дальнейших операций.
Пример реализации алгоритма поиска максимального значения:
number = 12345
number_str = str(number)
max_digit = int(number_str[0])
for digit_str in number_str:
digit = int(digit_str)
if digit > max_digit:
max_digit = digit
print("Максимальная цифра в числе:", max_digit)
В результате выполнения данного кода будет выведено значение "Максимальная цифра в числе: 5", так как в числе 12345 наибольшей цифрой является 5.
Данный алгоритм может быть полезен в различных задачах программирования, где требуется нахождение максимальной цифры в числе, например, при решении задач на программирование по анализу данных или обработке числовых последовательностей.
Математический подход

Еще один подход - преобразовать число в строку и итерироваться по символам строки. Преобразованная строка позволяет обрабатывать каждую цифру по отдельности и сравнивать их между собой. Сохраняйте максимальную цифру в отдельной переменной и сравнивайте каждую цифру с текущей максимальной цифрой. Если цифра больше, чем текущая максимальная цифра, обновите значение текущей максимальной цифры.
Оба метода дают вам возможность найти максимальную цифру в числе, используя математический подход. Выберите тот, который лучше подходит для вашей конкретной задачи и реализуйте его в своем коде.
Рекурсивный метод

Для реализации рекурсивного метода поиска максимальной цифры в числе необходимо определить базовый случай – крайнюю ситуацию, в которой функция прекратит вызывать себя и вернет результат. В данном случае базовым случаем может быть ситуация, когда число состоит из одной цифры.
Если число состоит из нескольких цифр, то функция рекурсивно вызывает саму себя для оставшейся части числа и сравнивает полученный результат с текущей цифрой числа. Затем функция возвращает максимум из полученных двух значений.
Пример:
function findMaxDigit(n) {
if (n В результате выполнения данного примера в консоль будет выведено сообщение: "Максимальная цифра числа 8675309: 9". Функция findMaxDigit рекурсивно вызывает саму себя для оставшейся части числа и сравнивает полученный результат с текущей цифрой числа, возвращая максимум из них.
Использование рекурсивного метода для поиска максимальной цифры в числе может быть полезным в случаях, когда требуется обработать каждую цифру числа в отдельности и выполнить операции с каждой из них.
Сравнение методов и выбор наиболее эффективного

При поиске максимальной цифры в числе существуют различные методы, которые можно использовать. Некоторые из них более эффективны с точки зрения времени выполнения, другие могут быть более простыми для понимания и реализации. В этом разделе мы рассмотрим несколько популярных методов и их преимущества.
- Метод перебора числа по цифрам: в этом методе число преобразуется в строку, а затем каждая цифра перебирается с помощью цикла. Сравнивая каждую цифру с текущей максимальной, мы можем найти максимальную цифру в числе. Этот метод прост для понимания и реализации, но может быть неэффективен на больших числах.
- Метод использования математических операций: в этом методе мы можем использовать операции деления нацело и остатка от деления для вычленения цифр числа. Затем мы можем сравнить каждую цифру с текущей максимальной, чтобы найти максимальную цифру. Этот метод более эффективен с точки зрения времени выполнения, но может быть сложнее для понимания и реализации.
- Метод использования массива цифр: в этом методе каждая цифра числа добавляется в массив, и затем мы можем найти максимальную цифру с помощью встроенных методов массивов, таких как
Math.max(). Этот метод может быть удобным, особенно если вы уже используете массивы в своем коде, но может быть неэффективным, если вам не нужен весь массив для других целей.
При выборе метода важно учитывать особенности вашего конкретного случая использования, а также уровень производительности, простоту реализации и понимания кода. Выберите метод, который наиболее подходит к вашим требованиям и условиям задачи.