Матрицы с пониженной размерностью – это инструмент, который позволяет сократить размерность данных, снижая количество переменных, сохраняя при этом важную информацию. Эта техника активно используется в различных областях, таких как обработка сигналов, статистика, компьютерное зрение и машинное обучение.
Одним из наиболее популярных методов понижения размерности является метод главных компонент (PCA). Он позволяет выделить наиболее значимые признаки в данных, удаляя "лишние" переменные. В основе этого метода лежит матричное представление данных, где строки матрицы соответствуют наблюдениям, а столбцы – признакам.
При использовании метода главных компонент значения в столбцах матрицы преобразуются таким образом, чтобы новые переменные были некоррелированы между собой и содержали максимально возможную информацию о данных. Таким образом, можно получить новую матрицу с меньшим количеством столбцов, которая сохранит основную структуру исходных данных и сократит объем вычислений.
Как найти матрицы с сниженной размерностью

Одним из популярных методов снижения размерности является использование метода главных компонент (PCA). Этот метод находит линейные комбинации исходных признаков, которые наиболее эффективно объясняют вариацию в данных. Результатом является новый набор признаков, называемый главными компонентами, который имеет меньшую размерность, но сохраняет максимально возможную информацию о данных.
Другим методом снижения размерности является t-SNE (t-distributed stochastic neighbor embedding). Он используется для визуализации высокоразмерных данных в двумерном или трехмерном пространстве. Он пытается сохранить геометрические отношения между объектами в исходном пространстве, сокращая размерность таким образом, чтобы объекты с похожими признаками были близко расположены, а объекты с разными признаками – далеко друг от друга.
Также существуют нейронные сети, способные выполнять нелинейное снижение размерности данных. Они используются для обработки исходных данных и создания нового набора признаков или представления данных с меньшей размерностью.
В конечном итоге, выбор метода снижения размерности зависит от задачи, данные которой нужно анализировать, и поставленных целей. Комбинация различных методов может быть использована для достижения оптимального результата.
Выбор подходящей размерности

Вероятностные методы понижения размерности
В задаче поиска матриц с пониженной размерностью важно выбрать подходящую размерность, которая позволит сохранить максимальное количество информации о данных при снижении их размерности. Одним из способов выбора подходящей размерности являются вероятностные методы.
Вероятностные методы позволяют моделировать зависимости между исходными и пониженными размерностями, и на их основе определять оптимальное значение для размерности матрицы.
Статистические методы понижения размерности
Кроме того, статистические методы понижения размерности также помогают выбрать подходящую размерность матрицы. Они используют статистические показатели, такие как дисперсия и среднее значение, для определения значимости каждой размерности.
Статистические методы позволяют определить, какие размерности содержат наиболее важную информацию о данных, и исключить из рассмотрения незначимые размерности.
Эвристические методы понижения размерности
Существуют также эвристические методы, которые основаны на эмпирических наблюдениях и эвристических правилах. Эти методы могут быть применимы в случаях, когда нет четкого понимания структуры данных и отсутствуют достоверные модели зависимостей между исходными и пониженными размерностями.
Эвристические методы позволяют проводить быстрый экспериментальный анализ и выбирать размерность матрицы на основе наиболее эффективных эвристик.
Анализ информационных потерь
При выборе подходящей размерности необходимо также учитывать информационные потери, связанные с понижением размерности. Для этого проводится анализ отношения между сохраняемой информацией и размерностью матрицы. Важно найти баланс между сохранением информации и снижением размерности, чтобы достичь наилучших результатов.
В итоге, выбор подходящей размерности матрицы с пониженной размерностью зависит от конкретной задачи, доступных данных и требуемого уровня информации.
Использование метода главных компонент
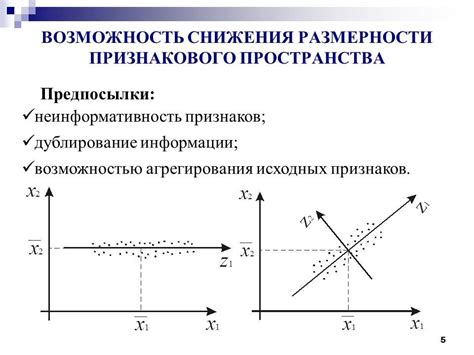
Применение метода главных компонент может быть полезным в таких случаях, как визуализация данных с большим числом признаков, удаление шума из данных или ускорение обработки данных.
Процесс PCA можно разделить на несколько шагов:
- Стандартизация данных: перед применением PCA необходимо стандартизировать данные, чтобы иметь средние значения равные 0 и стандартные отклонения равные 1.
- Вычисление ковариационной матрицы: ковариационная матрица позволяет вычислить степень зависимости между различными признаками. Она представляет собой квадратную симметричную матрицу размерности N x N, где N - количество признаков.
- Вычисление собственных векторов и собственных значений матрицы: собственные векторы и собственные значения матрицы ковариации являются основными характеристиками PCA и позволяют найти главные компоненты.
- Выбор главных компонент: на основе собственных значений выбираются самые информативные главные компоненты. Чем больше собственное значение, тем больше информации содержится в соответствующей главной компоненте.
- Проецирование данных на главные компоненты: данные преобразуются в новое пространство признаков, образованное главными компонентами.
Результатом применения метода главных компонент является матрица с пониженной размерностью, где количество столбцов соответствует выбранным главным компонентам.
Использование метода главных компонент позволяет существенно сократить размерность данных, сохраняя при этом основные характеристики и информацию. Это отличный инструмент для анализа и визуализации данных с множеством признаков.
Применение сингулярного разложения

Матрица U содержит левые сингулярные векторы, а матрица V содержит правые сингулярные векторы. Диагональная матрица Σ содержит сингулярные значения, которые показывают важность каждой компоненты матрицы.
Применение SVD позволяет нам выбрать наиболее значимые компоненты матрицы и отбросить менее значимые. Это позволяет уменьшить размерность матрицы и удалить шумовые данные.
Одним из наиболее распространенных применений SVD является сжатие и восстановление изображений. Путем сокращения размерности матрицы изображения с помощью SVD, мы можем значительно сэкономить место для хранения, не теряя значимой информации. Затем мы можем восстановить изображение, используя только наиболее важные компоненты.
Сингулярное разложение также находит применение в областях машинного обучения и анализа данных, где пространство признаков может быть сильно коррелировано. Понижение размерности с помощью SVD может улучшить производительность моделей и сократить время обучения.
Извлечение признаков с помощью дискриминантного анализа
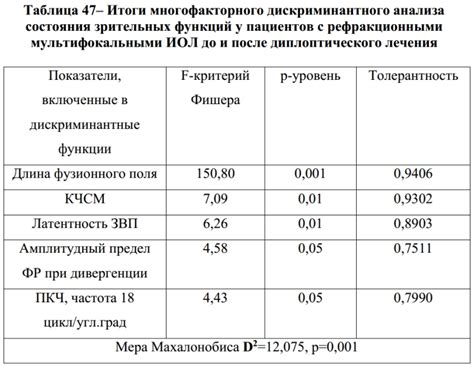
В контексте понижения размерности, дискриминантный анализ может быть использован для нахождения линейных комбинаций исходных признаков, которые наиболее эффективно разделяют классы. Эти комбинации называются дискриминантными осьми или признаковыми векторами.
Алгоритм дискриминантного анализа определяет такие признаки, которые максимизируют отношение разброса между классами к разбросу внутри классов. Для этого вычисляется матрица Scatter между классами и матрица Scatter внутри классов. Полученные матрицы используются для вычисления дискриминантных осей.
Когда все дискриминантные оси найдены, можно произвести проекцию исходных данных на низкоразмерное пространство, используя матрицу с пониженной размерностью. Это позволяет сохранить максимально возможную дискриминирующую информацию при одновременном уменьшении размерности данных.
Результаты дискриминантного анализа могут быть использованы в различных задачах машинного обучения, включая распознавание образов, классификацию данных и кластеризацию.
Таким образом, дискриминантный анализ представляет собой мощный инструмент для понижения размерности данных и извлечения наиболее информативных признаков для разделения классов.
Обратное преобразование для восстановления данных
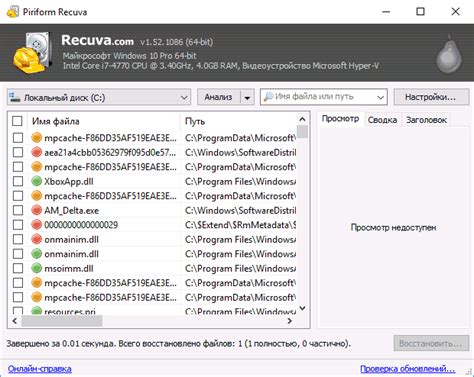
Для восстановления исходных данных из матрицы с пониженной размерностью необходимо выполнить обратное преобразование. Это можно сделать с использованием вектора весов или проекционной матрицы, полученных в результате снижения размерности. Процесс обратного преобразования сводится к умножению матрицы с пониженной размерностью на вектор весов или проекционную матрицу.
В результате обратного преобразования получается новая матрица, которая близка к исходным данным. Однако, необходимо учесть, что при снижении размерности и восстановлении данных происходит потеря некоторой информации. Поэтому, при восстановлении данных можно получить только приближенное представление исходных данных.
Обратное преобразование является важным шагом при использовании методов снижения размерности. Оно позволяет сохранить и анализировать основные характеристики данных с меньшим количеством признаков. Это особенно полезно, когда имеется большое количество признаков или необходимо убрать шумы и избыточность в данных.
Применение матриц с пониженной размерностью

Матрицы с пониженной размерностью широко применяются в различных областях, включая анализ данных, компьютерное зрение, обработку естественного языка и многое другое. Они позволяют сократить размерность данных, удаляя избыточные или неинформативные признаки, что упрощает последующий анализ и обработку данных.
Одно из основных применений матриц с пониженной размерностью - изображение сжатия. Путем снижения размерности матрицы пикселей, можно уменьшить объем информации, несмотря на сохранение основных характеристик изображения. Это позволяет сократить затраты на хранение и передачу данных и снизить временные затраты на обработку изображений.
Другой важной областью применения матриц с пониженной размерностью является обработка текстовых данных. Путем преобразования матрицы слов в матрицу с более низкой размерностью можно упростить анализ и классификацию текстов, снизить вычислительные затраты и улучшить качество моделей машинного обучения.
Матрицы с пониженной размерностью также применяются в задачах распознавания образов и сигналов. Сокращение размерности позволяет улучшить производительность алгоритмов обработки сигналов и повысить точность распознавания образов, что имеет большое практическое значение в таких областях, как компьютерное зрение, речевые технологии и биомедицинская инженерия.
| Область применения | Примеры |
|---|---|
| Анализ данных | Снижение размерности признаков, кластеризация данных |
| Компьютерное зрение | Сжатие и обработка изображений |
| Обработка текстовых данных | Улучшение качества моделей машинного обучения |
| Распознавание образов и сигналов | Повышение точности распознавания |
Все эти примеры подтверждают значимость и широкий спектр применения матриц с пониженной размерностью в различных областях науки и техники. Они позволяют сократить затраты на хранение и обработку данных, повысить производительность алгоритмов и улучшить качество результатов анализа и обработки информации.