Медиана - это линия, которая соединяет вершину прямоугольного треугольника с серединой противоположной стороны. В случае прямоугольного треугольника это означает, что медиана будет проходить через середину катета.

Найти медиану к катету в прямоугольном треугольнике можно используя теорему Пифагора. Если известны длины обоих катетов, то длина медианы будет равна половине гипотенузы. Это можно выразить следующей формулой:

медиана = 0.5 * √(катет1^2 + катет2^2)

Давайте рассмотрим пример расчета медианы к катету:

Задача: найти медиану к катету в прямоугольном треугольнике, где длина первого катета равна 4 единицы, а длина второго катета равна 3 единицы.

Используя формулу, подставим значения катетов в уравнение:

медиана = 0.5 * √(4^2 + 3^2)

Выполнив вычисления, получим:

медиана = 0.5 * √(16 + 9) = 0.5 * √25 = 0.5 * 5 = 2.5

Таким образом, медиана к катету в данном примере равна 2.5 единицы.

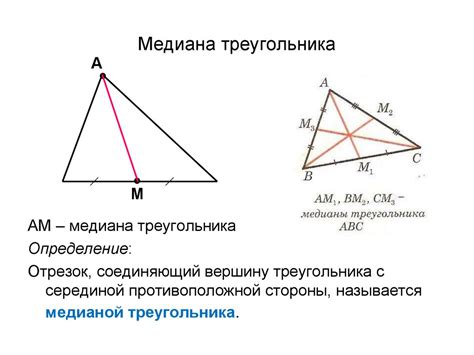
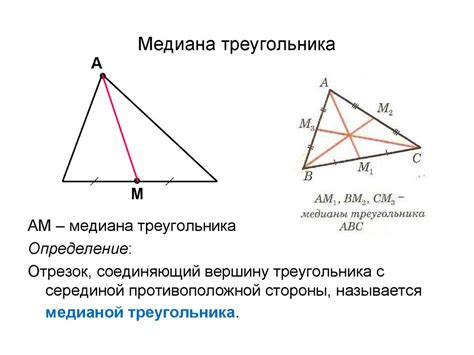
Определение медианы в прямоугольном треугольнике

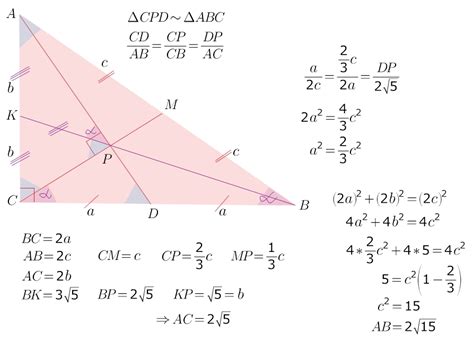
Для определения медианы в прямоугольном треугольнике, необходимо знать длину катета, которую обозначим как "a". Зная длину катета, мы можем вычислить длину медианы по формуле:

Медиана = a / 2

Приведем пример расчета медианы в прямоугольном треугольнике:

Пусть у нас есть прямоугольный треугольник ABC, где угол B - прямой угол. Длина катета AB равна 6. Найдем медиану, соединяющую вершину B с серединой стороны AC.

Сначала найдем длину стороны AC, используя теорему Пифагора:

AC^2 = AB^2 + BC^2

AC^2 = 6^2 + BC^2

AC^2 = 36 + BC^2

Так как BC - это второй катет прямоугольного треугольника, а его длина равна 8, подставляем значения в уравнение:

AC^2 = 36 + 8^2

AC^2 = 36 + 64

AC^2 = 100

AC = 10

Теперь, зная длину стороны AC, мы можем найти медиану, соединяющую вершину B с серединой стороны AC:

Медиана = AC / 2

Медиана = 10 / 2

Медиана = 5

Таким образом, медиана в прямоугольном треугольнике ABC, соединяющая вершину B с серединой стороны AC, равна 5.

Первый метод нахождения медианы к катету

Медиана к катету = (1/2) * длина катета

Для примера, рассмотрим прямоугольный треугольник со сторонами 3 и 4. Чтобы найти медиану к катету, нам нужно умножить длину катета на 0.5:

Медиана к катету = (1/2) * 3 = 1.5

Таким образом, медиана к катету в этом треугольнике равна 1.5.

Этот метод является простым и быстрым способом нахождения медианы к катету в прямоугольном треугольнике.

Второй метод нахождения медианы к катету

Второй метод нахождения медианы к катету в прямоугольном треугольнике основан на использовании теоремы Пифагора. Этот метод может быть полезен, когда недоступны точные значения длины сторон треугольника.

Для применения этого метода необходимо знать длины обоих катетов прямоугольного треугольника, а также прямой угол, образованный этими катетами.

Шаги для нахождения медианы к катету по второму методу:

1. Найдите длины обоих катетов прямоугольного треугольника. Пусть их длины будут a и b.
2. Используя теорему Пифагора, найдите гипотенузу треугольника.
3. Поделите длину гипотенузы пополам, чтобы найти медиану к катету.

Пример:

Пусть длина одного катета треугольника равна 4, а длина второго катета равна 3.

Используя теорему Пифагора, находим длину гипотенузы:

c = √(a² + b²) = √(4² + 3²) = √(16 + 9) = √25 = 5

Теперь делим длину гипотенузы пополам, чтобы найти медиану к катету:

медиана к катету = c/2 = 5/2 = 2.5

Таким образом, в данном примере медиана к катету прямоугольного треугольника равна 2.5.

Пример расчета медианы к катету по первому методу

Для расчета медианы к катету в прямоугольном треугольнике по первому методу, мы должны знать длины обоих катетов.

Рассмотрим следующую ситуацию: у нас есть прямоугольный треугольник ABC, где AB является горизонтальным катетом, BC - вертикальным катетом, а AC - гипотенузой.

Допустим, длина горизонтального катета AB равна 4 единицам, а длина вертикального катета BC равна 3 единицам.

Для расчета медианы к горизонтальному катету AB по первому методу, мы используем следующую формулу:

Медиана к катету AB = √(2 * BC² + AC²) / 2

Подставляя известные значения в формулу:

Медиана к катету AB = √(2 * 3² + 5²) / 2

Медиана к катету AB = √(2 * 9 + 25) / 2

Медиана к катету AB = √(18 + 25) / 2

Медиана к катету AB = √43 / 2

Медиана к катету AB ≈ 3.28 единиц

Таким образом, медиана к горизонтальному катету AB в данном прямоугольном треугольнике равна примерно 3.28 единицы.

Пример расчета медианы к катету по второму методу

Для расчета медианы к катету в прямоугольном треугольнике можно использовать второй метод, который основан на применении теоремы Пифагора. Этот метод позволяет найти медиану по формуле:

медиана = √(2 * катет² + гипотенуза²) / 2

Для наглядности приведем пример расчета медианы к катету на конкретном треугольнике:

1. Пусть у нас есть прямоугольный треугольник со значениями катета a = 5 и гипотенузы c = 13.
2. Применим формулу для расчета медианы: медиана = √(2 * 5² + 13²) / 2.
3. Выполним вычисления: медиана = √(2 * 25 + 169) / 2 = √(50 + 169) / 2 = √(219) / 2 ≈ √109.5 ≈ 10.47.

Таким образом, медиана к катету в данном прямоугольном треугольнике составляет примерно 10.47 единиц.

Обоснование выбора метода расчета медианы к катету

Расчет медианы к катету осуществляется с целью определения точки пересечения медианы с катетом, что позволяет изучать различные свойства треугольника.

Метод расчета медианы к катету, который следует выбирать, зависит от задачи, которую нужно решить.

Если известны длины катетов прямоугольного треугольника, можно использовать теорему Пифагора для нахождения длины гипотенузы. Затем, с использованием этой длины гипотенузы и известной длины одного из катетов можно рассчитать длину другого катета с помощью теоремы Пифагора или правила подобных треугольников.

Если известны два катета прямоугольного треугольника, можно использовать теорему Пифагора для нахождения длины гипотенузы. Затем, с использованием этой длины гипотенузы и известной длины одного из катетов можно рассчитать длину другого катета с помощью теоремы Пифагора или правила подобных треугольников.

Таким образом, выбор метода расчета медианы к катету зависит от данных, которые известны или которые требуется найти.