Медиана – это отрезок, соединяющий любую вершину треугольника с серединой противолежащей стороны. В правильном треугольнике все три медианы пересекаются в одной точке, называемой центром тяжести. Нахождение медианы треугольника является одной из основных задач в геометрии. В этой статье мы рассмотрим формулы и примеры расчета медианы правильного треугольника.
Формула для расчета медианы треугольника:
Медиана одного из углов показывает, какое расстояние нужно пройти из вершины до середины противолежащей стороны. Для ее расчета используется следующая формула: медиана = 0.5 * сторона.
Пример расчета медианы треугольника:
Допустим, у нас есть правильный треугольник со стороной длиной 10 см. Чтобы найти медиану, мы применяем формулу: медиана = 0.5 * 10 см = 5 см. Таким образом, медиана треугольника равна 5 см.
Использование формулы для расчета медианы позволяет легко находить эту характеристику правильного треугольника. Зная длину стороны, мы можем быстро определить длину медианы. Помните, что в правильном треугольнике все три медианы равны друг другу и пересекаются в центре тяжести.
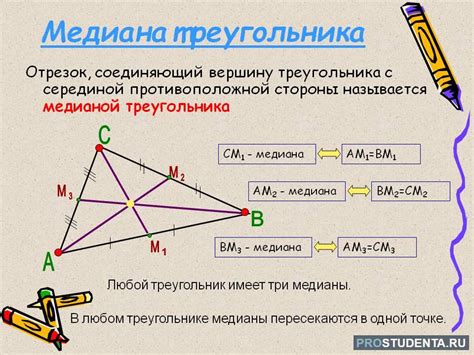
Что такое медиана правильного треугольника?
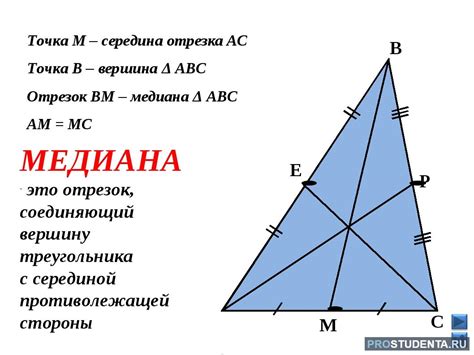
Медианы правильного треугольника делятся на две группы: внутренние и внешние. Внутренние медианы идут от вершин треугольника до центра масс, а внешние медианы идут от вершин треугольника до середины противоположной стороны во внешнюю сторону.
Медиана правильного треугольника является линией симметрии треугольника. Это означает, что медиана делит треугольник на две равные части площадью и равные по длине сторонами.
Расчет медианы правильного треугольника выполняется по формуле:
медиана = (сторона треугольника) * √3 / 2
Найдя медиану, можно вычислить также площадь правильного треугольника и другие важные параметры данной фигуры.
Как вычислить медиану правильного треугольника?
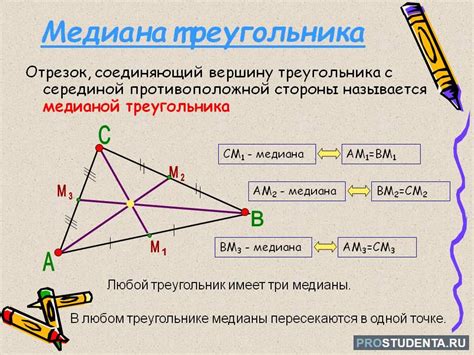
Чтобы вычислить медиану правильного треугольника, можно использовать формулу:
Медиана = (0,5 * сторона) / √3
Где:
- Медиана – длина медианы треугольника
- сторона – длина стороны треугольника
- √3 – квадратный корень из числа 3
Например, если известна длина стороны треугольника равная 6 см, то для расчета длины медианы необходимо выполнить следующие вычисления:
Медиана = (0,5 * 6) / √3 ≈ 2,6 см
Таким образом, длина медианы правильного треугольника со стороной 6 см будет приблизительно равна 2,6 см.
Вычисление медианы правильного треугольника имеет практическое применение в геометрии и строительстве, а также может быть использовано при решении задач по математике и физике.
Формула для расчета медианы правильного треугольника
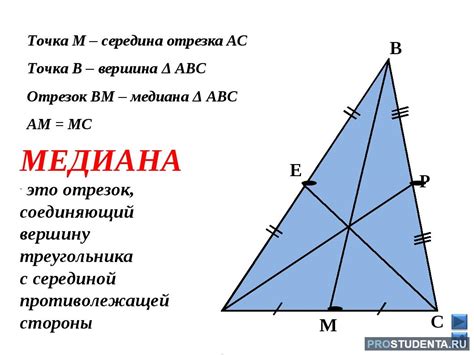
Пусть a - сторона правильного треугольника, а m - медиана, проведенная из одной из его вершин. Тогда формула для расчета медианы имеет вид:
m = (√3/2) * a
Если известна длина стороны треугольника, то для нахождения медианы достаточно умножить длину стороны на (√3/2).
Например, если сторона треугольника равна 6 см, то медиана будет:
m = (√3/2) * 6 ≈ 5.196 см
Таким образом, для правильного треугольника со стороной длиной 6 см, медиана будет примерно равна 5.196 см.
Примеры расчета медианы правильного треугольника
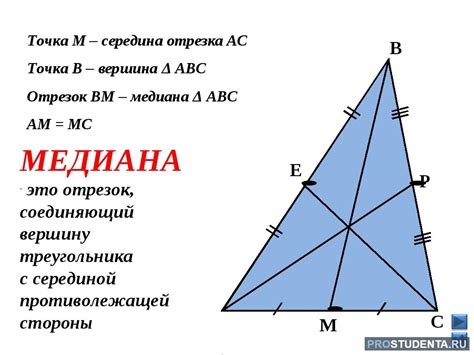
Для расчета медианы правильного треугольника используется следующая формула:
Медиана = (2/3) * a
где a - длина стороны треугольника.
Рассмотрим несколько примеров расчета медианы правильного треугольника:
Пример 1:
Длина стороны треугольника равна 6 см.
Медиана = (2/3) * 6 = 4 см.
Пример 2:
Длина стороны треугольника равна 12 м.
Медиана = (2/3) * 12 = 8 м.
Пример 3:
Длина стороны треугольника равна 5 дм.
Медиана = (2/3) * 5 = 10/3 дм.
Значение медианы правильного треугольника
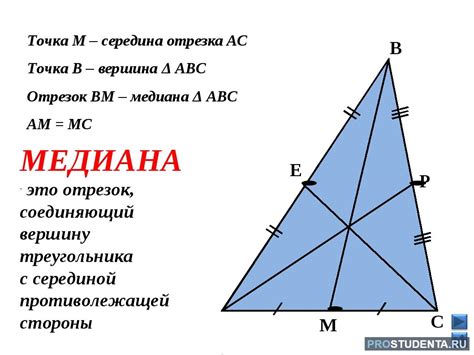
Для правильного треугольника со стороной a, формула для вычисления медианы (m) имеет вид:
| Формула: | m = (√3 / 2) * a |
Для лучшего понимания, рассмотрим пример. Предположим, что сторона правильного треугольника равна 6 см.
Используя формулу, мы можем вычислить значение медианы:
| a = 6 см | |
| m = (√3 / 2) * 6 | m ≈ 5.196 см |
Таким образом, значение медианы правильного треугольника со стороной 6 см составляет около 5.196 см.
Медианы правильного треугольника являются важными элементами данной геометрической фигуры и используются в различных математических и инженерных расчетах.
Задачи с медианой правильного треугольника
Задача 1:
Найдите медиану правильного треугольника, если длина стороны треугольника равна 12 см.
Решение:
В правильном треугольнике все медианы равны. Чтобы найти длину медианы, можно воспользоваться формулой:
медиана = (сторона треугольника) * sqrt(3) / 2
где sqrt(3) - корень из 3.
В данном случае, подставив значение стороны (12 см) в формулу, получим:
медиана = (12 см) * sqrt(3) / 2 ≈ 10.392 см
Ответ: медиана правильного треугольника ≈ 10.392 см.
Задача 2:
Известно, что медиана правильного треугольника равна 8 см. Найдите длину стороны треугольника.
Решение:
В правильном треугольнике все медианы равны. Чтобы найти длину стороны треугольника, можно воспользоваться обратной формулой:
сторона треугольника = (медиана) * 2 / sqrt(3)
где sqrt(3) - корень из 3.
Подставив значение медианы (8 см) в формулу, получим:
сторона треугольника = (8 см) * 2 / sqrt(3) ≈ 9.236 см
Ответ: длина стороны треугольника ≈ 9.236 см.
Важные свойства медианы правильного треугольника
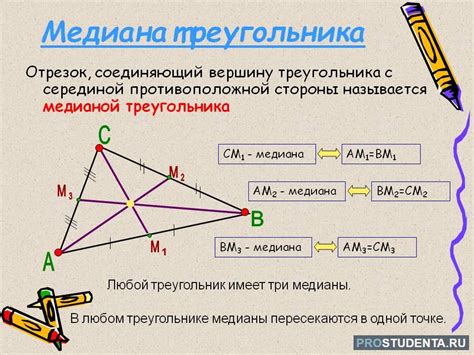
1. Делимость в отношении 2:1
Медиана правильного треугольника делит его стороны в отношении 2:1. Это означает, что отрезок, соединяющий вершину треугольника с серединой противолежащей стороны, будет иметь длину в два раза меньше, чем сторона треугольника. Например, если сторона треугольника равна 6 единицам длины, то медиана будет равна 3 единицам.
2. Пересечение в одной точке
Медианы правильного треугольника пересекаются в одной точке, называемой центром тяжести (центр масс). Этот центр является точкой равновесия, где сумма моментов всех сил относительно этой точки равна нулю. Он делит каждую медиану в отношении 2:1, то есть расстояние от вершины до центра масс будет в два раза больше, чем расстояние от центра масс до середины противолежащей стороны.
3. Центр масс как точка поддержки
Центр масс правильного треугольника является точкой поддержки, на которой он может покоиться в равновесии на горизонтальной плоскости. Если на треугольник действует вертикальная сила с центром приложения, проходящим через центр масс, треугольник будет оставаться в равновесии без поворота.
Медианы правильного треугольника обладают этими важными свойствами, которые широко применяются в геометрии и механике.