Прямоугольные треугольники – это одна из основных геометрических фигур, с которыми мы сталкиваемся в математике и физике. Если у вас есть прямоугольный треугольник с известными катетами, вы можете найти его медиану, которая является линией, соединяющей середины двух сторон треугольника.

Итак, как найти медиану прямоугольного треугольника? Существует несколько шагов, которые помогут вам сделать это. Во-первых, определите длины катетов треугольника. Обозначим их как a и b.

Далее, используя теорему Пифагора, найдите длину гипотенузы треугольника, которая будет равна корню из суммы квадратов длин катетов: \(\sqrt{a^2 + b^2}\). Теперь у вас есть все необходимые данные для нахождения медианы прямоугольного треугольника.

Как найти медиану прямоугольного треугольника:

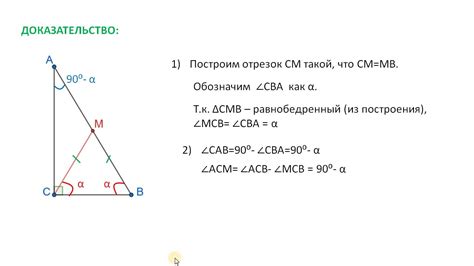
Для нахождения медианы треугольника, нужно выполнить следующие шаги:

1. Найдите длины обоих катетов треугольника.
2. Найдите середину противоположной стороны. Для этого можно использовать формулу для нахождения середины отрезка: (x1+x2)/2, (y1+y2)/2, где (x1, y1) и (x2, y2) - координаты концов отрезка.
3. Проведите линию из вершины прямого угла до середины противоположной стороны. Это и будет медиана треугольника.

Медиана является важной характеристикой треугольника, и ее можно использовать для расчета площади, высоты и других параметров треугольника. Также она является линией симметрии и делит треугольник на две равные части.

Шаг 1: Определение известных катетов

Прямоугольный треугольник имеет два катета и гипотенузу. Для нахождения медианы нам необходимо знать значения обоих катетов.

Катеты - это две стороны треугольника, которые образуют прямой угол. Обозначим их как a и b.

Чтобы определить значения катетов, мы можем использовать следующие данные:

1. Заданный угол. Если мы знаем значение угла, можно использовать тригонометрические функции (тангенс, синус или косинус) для нахождения катетов.
2. Длины других сторон треугольника. Если мы знаем длины гипотенузы и одного катета, можно использовать теорему Пифагора (a^2 + b^2 = c^2) для нахождения второго катета.
3. Геометрические условия. Если мы знаем, что треугольник является прямоугольным, мы можем вычислить длины катетов с помощью геометрических свойств.

Прежде чем продолжить с нахождением медианы, убедитесь, что у вас есть достаточно информации для определения значений катетов. Если это не так, обратитесь к задаче или соберите дополнительные сведения.

Шаг 2: Нахождение гипотенузы

Для нахождения гипотенузы используется теорема Пифагора:

гипотенуза = √(катет1² + катет2²)

Где катет1 и катет2 – длины известных катетов прямоугольного треугольника, которые можно найти в предыдущих шагах.

Подставляем известные значения катетов в формулу и вычисляем:

гипотенуза = √(катет1² + катет2²)

Полученное значение гипотенузы будет использоваться в следующих шагах для нахождения медианы прямоугольного треугольника.

Шаг 3: Вычисление медианы

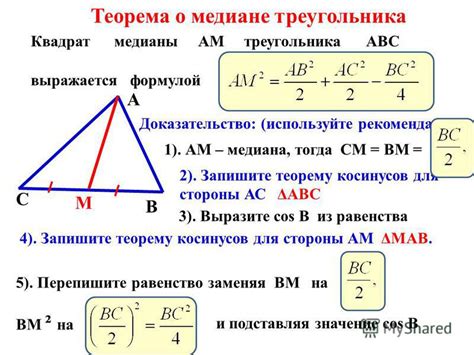
Для вычисления медианы прямоугольного треугольника с известными катетами, мы можем использовать формулу:

Медиана треугольника равна половине длины гипотенузы.

Выражение для вычисления медианы можно записать следующим образом:

Медиана = Гипотенуза / 2

Для того чтобы найти медиану, нужно поделить длину гипотенузы на 2.

Например, если длина гипотенузы равна 10 единицам, то медиана будет равна 5 единицам.

Вычисление медианы является важным шагом в решении задач, связанных с прямоугольными треугольниками. Она позволяет найти точку пересечения медиан треугольника и использовать ее для решения дополнительных задач, например, для нахождения центра масс треугольника.