Медиана равнобедренного треугольника - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. То есть, медианы равнобедренного треугольника делят его на две равные части. Важно знать, что в равнобедренном треугольнике все три медианы равны.
Чтобы найти медиану равнобедренного треугольника, необходимо сначала определить координаты точек вершин треугольника, затем найти середину противоположной стороны и соединить ее с вершиной треугольника. Можно воспользоваться формулами геометрии, чтобы вычислить координаты середины стороны.
Для формулы медианы равнобедренного треугольника нужно знать координаты вершин треугольника. Пусть точки A, B и C - вершины треугольника, а точка D - середина основания. Тогда координаты точек задаются так:
A(x₁, y₁)
B(x₂, y₂)
C(x₃, y₃)
Медиана: определение и свойства

Свойства медианы:
| 1. | Три медианы треугольника пересекаются в одной точке, называемой точкой пересечения медиан. |
| 2. | Точка пересечения медиан делит каждую медиану в отношении 2:1. То есть, если обозначить точку пересечения медиан как Г, а соответствующие отрезки как AG и ГM, то AG = 2ГM. |
| 3. | Точка пересечения медиан является центром тяжести треугольника. Это означает, что если подвесить треугольник за точку пересечения медиан, он будет равновесно висеть. |
| 4. | Медиана треугольника делит его площадь на две равные части. |
| 5. | Из двух сторон треугольника медиана всегда больше и не может быть равна ни одной из них. |
Медиана является важным элементом в геометрии и находит свое применение в различных задачах и теоремах, связанных с треугольниками.
Что такое медиана в геометрии
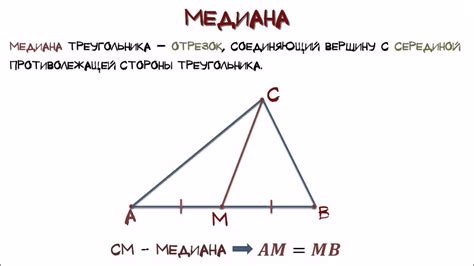
Основное свойство медианы заключается в том, что она делит треугольник на две равные по площади фигуры. Точка пересечения медиан называется центром тяжести или барицентром треугольника. Она является точкой равновесия, так как в ней сосредоточена половина всей массы треугольника.
Медианы в равнобедренном треугольнике, как и в любом другом треугольнике, также сходятся в одной точке - центре тяжести. Однако, в равнобедренном треугольнике медиана, проведенная из вершины угла, соответствующего основанию равнобедренности, будет совпадать с высотой треугольника и биссектрисой этого угла.
Геометрические свойства равнобедренного треугольника
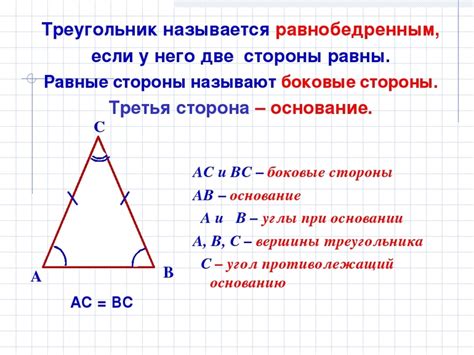
Главное геометрическое свойство равнобедренного треугольника заключается в том, что углы при основании, образующиеся между основанием и боковыми сторонами, равны между собой. Такие углы называются углами при основании.
Это свойство можно использовать, чтобы решать задачи на нахождение углов и сторон равнобедренного треугольника. Например, если известна мера одного угла при основании, то из равенства этого угла с другим углом при основании можно найти меру обоих углов. А зная меру угла при основании и длину боковой стороны, можно найти длину основания и другую боковую сторону с помощью тригонометрических соотношений.
Геометрические свойства равнобедренного треугольника позволяют проводить разнообразные построения. Например, можно построить высоту, проведенную из вершины до основания, которая будет являться биссектрисой, медианой и медиатрисой треугольника. Кроме того, можно провести точку пересечения биссектрис и медиан треугольника - центр вписанной окружности.
Как построить медиану равнобедренного треугольника
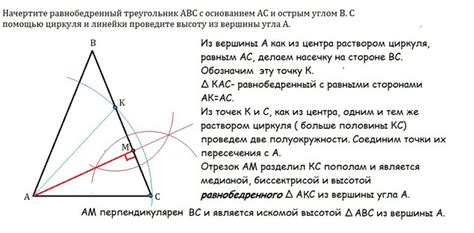
- Возьмите линейку и карандаш.
- Выберите любую вершину треугольника и назовите ее A.
- На линейке измерьте расстояние от вершины A до середины противоположной стороны. Назовите это расстояние d.
- На линейке отметьте расстояние d.
- Проведите прямую линию от вершины A через отмеченную точку на противоположной стороне.
- Проделайте те же шаги для двух других вершин треугольника.
- Точка пересечения трех построенных линий будет являться серединой треугольника и является концом медианы.
Таким образом, вы сможете построить медиану равнобедренного треугольника. Помните, что медианы в равнобедренных треугольниках равны друг другу и проходят через точку пересечения высот и центра описанной окружности треугольника.
Связь медианы с основанием равнобедренного треугольника
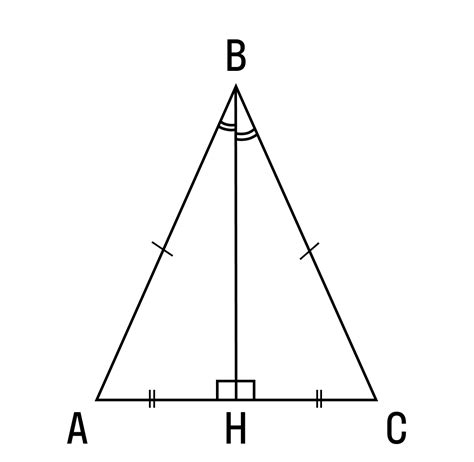
Важной особенностью равнобедренного треугольника является то, что медианы и основание треугольника образуют прямоугольный треугольник. Точка пересечения медиан, называемая центром тяжести, делит каждую медиану в отношении 2:1. Один отрезок медианы равен половине основания треугольника.
Таким образом, длина медианы равна половине длины основания равнобедренного треугольника.
Пример:
Рассмотрим равнобедренный треугольник ABC. Пусть AB = AC = 6 см. Основание треугольника равно BC. Чтобы найти длину медианы, нужно разделить длину основания пополам: BC/2. В данном случае, BC/2 = 3 см.
Таким образом, медиана равнобедренного треугольника ABC равна 3 см.
Формула нахождения длины медианы равнобедренного треугольника
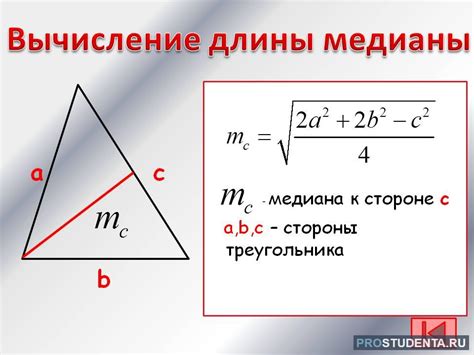
Длина медианы равнобедренного треугольника может быть найдена с использованием формулы:
m = √(2b² + a²)/2
где m - длина медианы, a - длина основания, b - длина боковой стороны (равной длине).
Эта формула позволяет найти длину медианы равнобедренного треугольника, зная длину его основания и боковой стороны. При вычислении необходимо заменить значения в формуле и выполнить соответствующие математические операции для получения результата.
Практическое применение медианы в задачах 7 класса
Одно из практических применений медианы в задачах 7 класса является определение центра тяжести равнобедренного треугольника. Центр тяжести представляет собой точку пересечения медиан. Он может быть использован для определения точки, вокруг которой треугольник может вращаться без изменения своего положения. Это свойство может быть полезным, например, при проектировании мостов или строительстве сооружений.
Другое применение медианы в задачах 7 класса - определение площади треугольника. Если известны длины медиан и одной стороны треугольника, то площадь треугольника можно вычислить с помощью формулы Герона.
Также медиана может быть использована для нахождения высоты равнобедренного треугольника. Высота представляет собой отрезок, опущенный из вершины треугольника на основание и перпендикулярный ему. Известно, что высота, проведенная к основанию треугольника, является медианой, а другая высота делит медиану и основание пополам. Это свойство медианы может быть использовано для нахождения высоты треугольника в задачах 7 класса.
Таким образом, медиана является полезным инструментом при решении задач, связанных с равнобедренными треугольниками. Знание свойств и применение медианы позволяет решать задачи более эффективно и точно.
Сводка результатов и полезные советы по нахождению медианы равнобедренного треугольника

- Медиана делит основание равнобедренного треугольника на две равные части.
- Медиана перпендикулярна основанию треугольника.
- Медиана также является биссектрисой, делящей угол при вершине треугольника на два равных угла.
- Точка пересечения медиан называется центром тяжести треугольника и делит каждую медиану в отношении 2:1 относительно вершины.
- Длина каждой медианы равна половине длины основания треугольника.
Чтобы найти медиану равнобедренного треугольника, можно воспользоваться следующим алгоритмом:
- Найдите середину противоположной стороны равнобедренного треугольника.
- Соедините вершину треугольника с найденной серединой прямой.
- Таким образом, получите медиану равнобедренного треугольника.
Помните, что медиана равнобедренного треугольника имеет ряд особенностей, которые можно использовать для упрощения решения задач. Знание этих особенностей поможет вам успешно решать задачи, связанные с нахождением медианы равнобедренного треугольника.