Медиана равнобедренного треугольника - это сегмент, соединяющий вершину треугольника с серединой противоположной стороны. Нахождение медианы является важной задачей в геометрии и может быть полезно при решении различных задач и конструкций.
Для того чтобы найти медиану равнобедренного треугольника, требуется знание периметра треугольника и длин боковой стороны. В этом руководстве мы рассмотрим подробный алгоритм поиска медианы с помощью простых математических формул.
Шаг 1: Определите периметр треугольника. Периметр - это сумма длин всех сторон треугольника. Обозначим периметр как "P".
Шаг 2: Выразите длины боковых сторон треугольника через переменные. Обозначим одну из боковых сторон как "a" и другую как "b". Так как треугольник равнобедренный, то "a" и "b" будут равными.
Шаг 3: Найдите полупериметр. Полупериметр равнобедренного треугольника равен половине периметра. Обозначим полупериметр как "s". Вычислим его по формуле: s = P / 2.
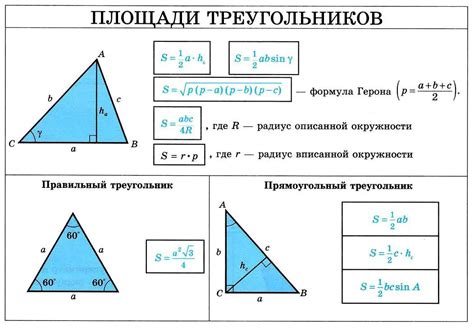
Шаг 4: Найдите длину медианы. Для нахождения длины медианы равнобедренного треугольника использовать следующую формулу: m = sqrt((2b^2 + 2a^2 - a^2 - b^2)/4), где "m" - длина медианы, "sqrt" - квадратный корень, "^" - символ возведения в степень.
Теперь вы знаете, как найти медиану равнобедренного треугольника по периметру. Обратите внимание, что в данной статье мы рассмотрели только случай равнобедренного треугольника. Для других типов треугольников существуют другие методы вычисления медианы.
Что такое медиана треугольника?

Медианы треугольника являются важными элементами геометрии и обладают несколькими свойствами. Например, все три медианы пересекаются в одной точке, называемой центром тяжести или центроидом треугольника. Это значит, что если мы нарисуем все три медианы, они встретятся в одной точке. Центроид является точкой равновесия, так как в равнобедренном треугольнике расстояние от центроида до каждой вершины треугольника одинаково.
Медианы также полезны при расчете многих параметров треугольника, включая его площадь и длины сторон. Например, медиана делит каждую сторону треугольника на две равные части, поэтому ее длина равна половине длины стороны, которую она пересекает. Это свойство медианы позволяет использовать ее для нахождения других параметров треугольника, таких как площадь или радиус вписанной окружности.
Медианы треугольника являются важными средствами для изучения различных свойств треугольников и могут быть использованы при решении задач и построении графиков. Их геометрические свойства помогают нам лучше понять структуру и характеризовать треугольники.
Как найти периметр равнобедренного треугольника?

Для определения периметра равнобедренного треугольника необходимо знать длину его стороны. В данном случае мы предполагаем, что уже имеется информация о равных сторонах треугольника.
Периметр равнобедренного треугольника можно вычислить, умножив длину равной стороны на 2 и прибавив к этому результату длину третьей стороны треугольника. Сумма сторон треугольника дает нам его периметр.
Если, к примеру, известна длина равной стороны треугольника (a) и длина третьей стороны (b), то периметр равнобедренного треугольника (P) можно выразить следующей формулой:
- P = 2a + b
Применяя данную формулу, можем легко определить периметр равнобедренного треугольника, зная длину равной стороны и длину третьей стороны.
Формула для расчета медианы по периметру
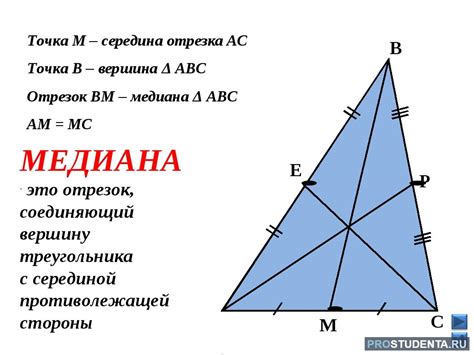
Медиана = (периметр / 2) × (1 / √3)
Где:
- Медиана - длина медианы равнобедренного треугольника, измеряемая в условных единицах;
- Периметр - сумма длин всех сторон треугольника, также измеряемая в условных единицах;
- √3 - квадратный корень из числа 3.
Используя данную формулу, вы сможете точно расчитать медиану равнобедренного треугольника, исходя из его периметра. Это позволит вам легко определить длину медианы и использовать эту информацию по вашему усмотрению.
Обратите внимание, что данная формула применяется только для равнобедренных треугольников.
Шаги по нахождению медианы равнобедренного треугольника
- Определите длину основания. Основание равнобедренного треугольника – это отрезок, соединяющий две равные стороны. Измерьте этот отрезок с помощью линейки.
- Найдите длины боковых сторон. В равнобедренном треугольнике боковые стороны равны друг другу. Измерьте одну из этих сторон с помощью линейки, затем удвойте эту длину, чтобы получить общую длину обеих боковых сторон.
- Рассчитайте периметр. Периметр равнобедренного треугольника – это сумма длин всех его сторон. Для этого сложите длины основания и обеих боковых сторон.
- Определите середину основания. Чтобы найти середину основания, разделите длину основания на 2.
- Проведите медиану. Используя середину основания как точку отсчета, нарисуйте отрезок, проходящий через вершину треугольника и середину основания. Этот отрезок является медианой равнобедренного треугольника.
Теперь вы знаете, как найти медиану равнобедренного треугольника по его периметру. Следуйте этим шагам и вы сможете легко рассчитать и построить медиану для любого равнобедренного треугольника.