Как найти медиану равностороннего треугольника с известной стороной

Медиана равностороннего треугольника - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Одно из основных свойств медианы заключается в том, что она делит сторону треугольника, к которой она проведена, пополам. Если известна длина стороны равностороннего треугольника, можно легко найти длину медианы, используя теорему Пифагора.

Чтобы узнать длину медианы равностороннего треугольника с известной стороной, нужно сперва найти длину этой стороны. Для этого можно воспользоваться формулой, которая позволяет вычислить длину стороны равностороннего треугольника по его площади. Далее, найдя длину стороны, можно применить теорему Пифагора, чтобы определить длину медианы.

Пример:

1. Пусть сторона равностороннего треугольника равна 6 см. Вычислим его площадь с помощью формулы: S = sqrt(3) * a^2 / 4, где а - длина стороны.
2. Подставляем значение стороны в формулу: S = sqrt(3) * 6^2 / 4 = 9√3.
3. Теперь, зная площадь треугольника, можем вычислить его высоту по формуле: h = (2 * S) / a.
4. Подставляем значения: h = (2 * 9√3) / 6 = 3√3.
5. Так как медиана равностороннего треугольника равна 2/3 высоты треугольника, длина медианы будет 2/3 * 3√3 = 2√3.

Таким образом, медиана равностороннего треугольника со стороной 6 см равна 2√3 см.

Медиана равностороннего треугольника с известной стороной

Для нахождения медианы равностороннего треугольника с известной стороной можно воспользоваться следующей формулой:

Медиана = (2/3) * (длина стороны треугольника)

Например, если сторона треугольника равна 6 см, то медиана равна:

Медиана = (2/3) * 6 см = 4 см

Таким образом, медиана равностороннего треугольника с известной стороной длиной 6 см равна 4 см. Отсчитывая эту медиану от одной из вершин треугольника, мы найдем середину противоположной стороны.

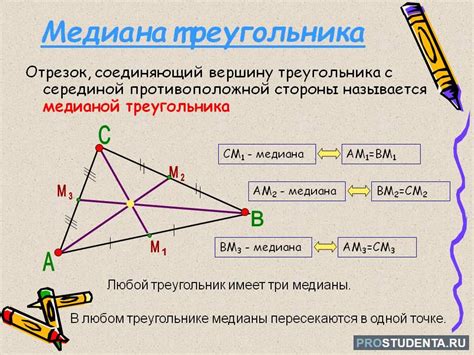
Определение и свойства медианы треугольника

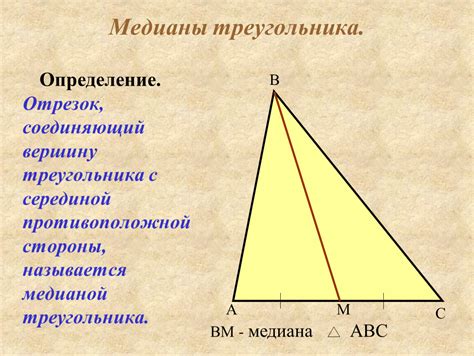
Медианы треугольника имеют несколько важных свойств:

• В треугольнике каждая из трех медиан делит другие две медианы в отношении 2:1. Это означает, что точка пересечения медиан делит каждую из них в отношении 2:1.
• Медианы треугольника пересекаются в одной точке, которая называется центром тяжести треугольника. Это точка, в которой располагается плоская масса треугольника. Центр тяжести треугольника является точкой баланса и ситуируется на каждой из трех медиан на расстоянии 2/3 от вершины и 1/3 от середины противоположной стороны.
• Медианы треугольника являются отрезками прямых линий и всегда пересекаются внутри треугольника.
• Медиана треугольника также является одной формой симметрии треугольника, разделяя треугольник на две равные площади.

Изучение медианы треугольника важно для понимания его структуры и свойств, а также для решения различных геометрических задач, связанных с треугольниками.

Равносторонний треугольник: основные характеристики

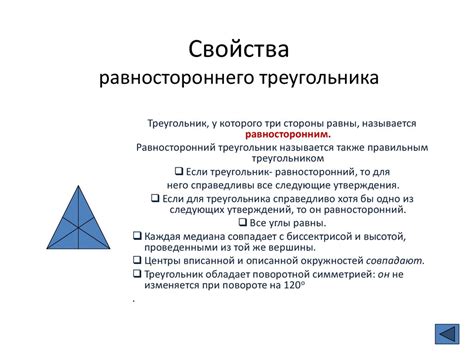
Основные характеристики равностороннего треугольника:

• Сторона: длина всех трех сторон равна. Обозначается буквой a.
• Угол: каждый угол равен 60 градусов. Обозначается буквой α.
• Высота: проведенная из вершины к основанию. Обозначается буквой h.
• Медиана: отрезок, соединяющий вершину с серединой противоположной стороны. Обозначается буквой m.
• Центр: пересечение медиан треугольника, обозначается буквой O.

Равносторонний треугольник имеет ряд интересных свойств:

• Все его высоты, медианы и биссектрисы являются одной и той же линией.
• Центр медиан совпадает с центром окружности, вписанной в треугольник.
• Радиус вписанной окружности равен трети от высоты треугольника.
• Радиус описанной окружности равен длине любой из сторон треугольника.

Эти характеристики позволяют легко вычислить длину стороны и другие параметры равностороннего треугольника, что является основой для решения разнообразных математических задач.

Способы определения медианы равностороннего треугольника

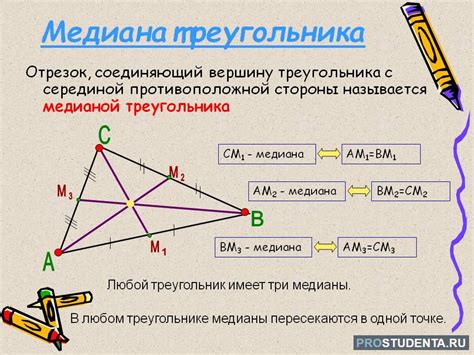
1. Первый способ основан на использовании свойств равностороннего треугольника. Для определения медианы можно воспользоваться теоремой Пифагора. В равностороннем треугольнике длина медианы составляет половину длины стороны треугольника. Например, если известна длина стороны треугольника, то длина медианы будет равна половине этой длины.
2. Второй способ основан на использовании формулы для определения медианы в равностороннем треугольнике. Формула для расчета длины медианы: m = \frac{a}{2}, где m - длина медианы, a - длина стороны треугольника. Используя эту формулу, можно легко определить длину медианы при известной длине стороны треугольника.
3. Третий способ основан на использовании геометрических построений. Для определения медианы равностороннего треугольника можно провести линию из вершины к середине противоположной стороны. Затем, построив перпендикуляр к этой линии из середины противоположной стороны, можно найти точку пересечения перпендикуляра и медианы. Таким образом, будет найдена середина медианы и определена ее длина.

Используя описанные способы, можно определить медиану равностороннего треугольника с известной стороной. Уверенность в правильности результата возрастет при применении нескольких способов и сравнении полученных значений. Знание медианы равностороннего треугольника может быть полезным при решении различных геометрических задач и вычислениях.

Вычисление длины медианы с известной стороной

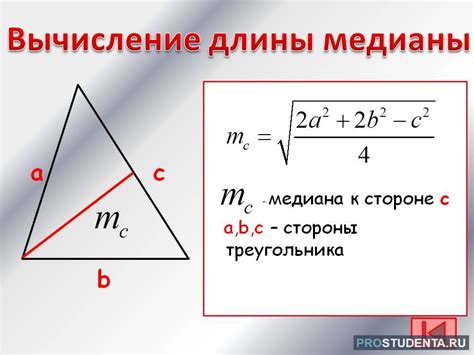
Его длина равна половине длины стороны треугольника.

Для вычисления длины медианы с известной стороной необходимо выполнить следующие шаги:

1. Определить длину стороны треугольника, для которой требуется найти медиану. Обозначим ее как a.
2. Вычислить длину медианы, используя формулу: медиана = a / 2.
3. Полученный результат является искомой длиной медианы.

Пример:

• Пусть дан равносторонний треугольник со стороной a = 6 см.
• Вычислим длину медианы: медиана = 6 / 2 = 3 см.
• Таким образом, длина медианы равно 3 см.

Таким образом, для вычисления длины медианы с известной стороной необходимо разделить длину стороны треугольника на 2.

Пример задачи на нахождение медианы треугольника

Допустим, у нас есть равносторонний треугольник со стороной длиной 6 см. Нам нужно найти медиану треугольника.

Медиана - это линия, которая соединяет вершину треугольника с серединой противоположной стороны. В равностороннем треугольнике все три медианы равны.

Чтобы найти медиану треугольника, мы можем использовать формулу:

1. Найдите половину длины стороны треугольника, то есть 6/2 = 3 см.
2. Проведите линию из вершины треугольника к середине противоположной стороны, образуя медиану.
3. Измерьте длину медианы. В данном случае, медиана будет равна 3 см.

Таким образом, медиана равностороннего треугольника со стороной длиной 6 см составляет 3 см.