Медиана равностороннего треугольника - одна из наиболее интересных характеристик этой геометрической фигуры. Медиана является отрезком, соединяющим вершину треугольника с серединой противолежащей стороны. Равносторонний треугольник имеет все три стороны равной длины, поэтому его медиана также обладает рядом особенностей, которые мы рассмотрим в данной подробной инструкции.
Получение медианы равностороннего треугольника включает несколько шагов:
- Найдите середину противолежащей стороны треугольника.
- Соедините эту точку с вершиной треугольника.
- Отметьте середину получившегося отрезка – это и будет медиана равностороннего треугольника.
Данная инструкция проста и понятна даже для начинающих. Следуя этим шагам, вы сможете легко найти медиану равностороннего треугольника. Дальнейшее использование медианы позволит осуществлять различные геометрические построения и решать задачи. Применяйте полученные знания на практике и укрепляйте свои навыки в области геометрии!
Что такое медиана равностороннего треугольника
Медианы равностороннего треугольника являются особенными, так как они делятся пополам другими медианами и отрезают одинаковое количество площади от каждой стороны треугольника. В результате, точка пересечения медиан является центром симметрии треугольника и также центром тяжести. Это означает, что равносторонний треугольник может быть уравновешен на острие своей медианы.
Медиана равностороннего треугольника является важным геометрическим понятием и лежит в основе различных математических и физических рассуждений. Ее длина может быть вычислена с использованием определенных формул или геометрических конструкций. Знание о медианах позволяет решать задачи, связанные с центром равностороннего треугольника, его углами, сторонами и площадью.
Концепция медианы
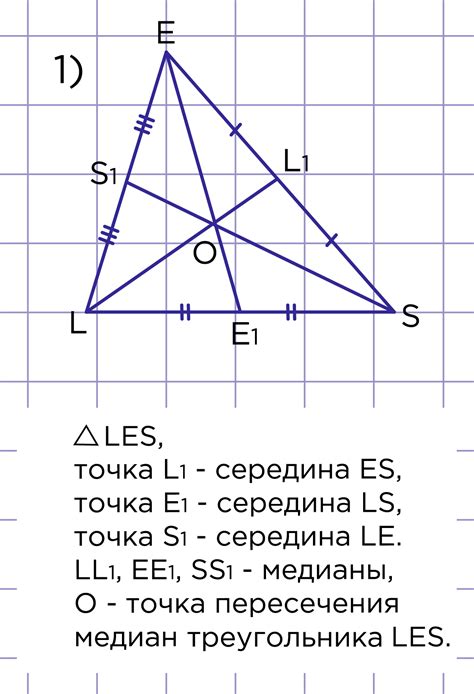
Центр масс треугольника является точкой пересечения всех трех медиан и обладает рядом удивительных свойств. Во-первых, отрезки медиан, соединяющие вершины треугольника с центром масс, равны друг другу и делятся в отношении 2:1, то есть длина отрезка, соединяющего вершину треугольника и центр масс, вдвое больше, чем длина отрезка, соединяющего центр масс с серединой противолежащей стороны треугольника.
Кроме того, центр масс является точкой баланса треугольника, то есть если треугольник вешать на центр масс, он будет равновесно висеть горизонтально. Это свойство используется в различных областях, например, при конструировании многоугольников или анализе прочности треугольных конструкций.
Таким образом, понимание концепции медианы и центра масс равностороннего треугольника является важным для решения различных задач в геометрии и строительстве.
Определение медианы треугольника
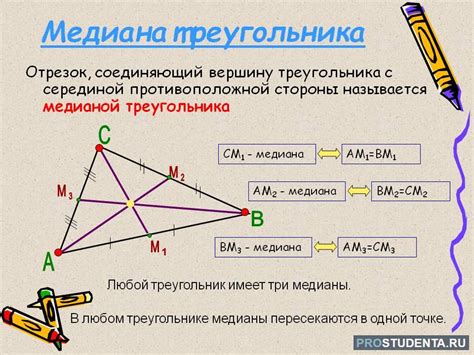
Для более наглядного представления, можно представить медианы треугольника в виде "тянущейся" силы. Каждая медиана действует как ось вращения, соединяя вершину треугольника с серединой противоположной стороны. Когда мы имеем дело с равносторонним треугольником, медианы сходятся в одной точке, что является особенностью равносторонних треугольников.
Центр масс треугольника, также называемый "тотальным центром" или "барицентром", располагается в точке пересечения медиан. Эта точка представляет собой центр массы треугольника и является особенно важной в физических расчетах и геометрических задачах.
Понимание медиан треугольника позволяет лучше понять его структуру и свойства. Зная, что медианы делятся в отношении 2:1, мы можем использовать эту информацию для решения геометрических задач, таких как нахождение площади или периметра равностороннего треугольника или нахождение положения его центра массы. Медианы также могут использоваться для нахождения высоты треугольника и решения аналогичных задач.
Свойства равностороннего треугольника

1. Углы равностороннего треугольника равны между собой и составляют по 60 градусов. Это означает, что каждый угол равностороннего треугольника составляет 1/3 от 180 градусов.
2. Основание равностороннего треугольника - это любая из его сторон. Все стороны равностороннего треугольника могут служить основанием. При этом, высота, опущенная из вершины, перпендикулярна основанию и делит его пополам.
3. В равностороннем треугольнике все высоты, медианы и биссектрисы равны между собой. Это означает, что, например, все медианы равностороннего треугольника делятся друг на друга в отношении 1:2.
4. Площадь равностороннего треугольника можно вычислить, зная длину его сторон. Формула для вычисления площади равностороннего треугольника: S = (a^2 * sqrt(3)) / 4, где a - длина стороны.
5. Равносторонний треугольник имеет описанную около него окружность, центр которой совпадает с центром треугольника. Радиус этой окружности равен половине длины стороны.
Зная эти свойства, можно более глубоко изучить и понять природу равностороннего треугольника и его характеристики.
Основные характеристики равностороннего треугольника

1. Равносторонний треугольник имеет три равных стороны. Это значит, что длина каждой стороны равна.
2. Все углы равностороннего треугольника также равны между собой. Каждый угол равен 60 градусов.
3. Равносторонний треугольник является правильным многоугольником. Правильные многоугольники имеют все стороны и углы равными.
4. Центральная симметрия – это еще одна характеристика равностороннего треугольника. Если проследить за линией, соединяющей вершины треугольника и проходящей через его центр, каждый из трех треугольников, образованных этой линией, является равнобедренным треугольником.
5. Равносторонний треугольник имеет также связь с равносторонними геометрическими фигурами, такими как шестиугольник и додекаэдр. Все эти фигуры имеют равные стороны и углы.
Как найти медиану равностороннего треугольника
- Нарисуйте равносторонний треугольник на листе бумаги или в программе для рисования.
- Выберите любую сторону треугольника и пометьте ее середину, например, точку "М".
- Соедините вершину треугольника, которая не лежит на выбранной стороне, с помеченной серединой. Эта линия будет медианой.
- Повторите шаги 2 и 3 для каждой стороны треугольника. В результате вы получите три медианы, которые пересекутся в одной точке. Эта точка называется центром равностороннего треугольника.
Медиана равностороннего треугольника делит его на три равные части, а также проходит через центр масс треугольника. Это полезное свойство треугольника, которое может использоваться в геометрии, физике и других науках.
Шаг 1: Нарисовать равносторонний треугольник
Первым шагом необходимо нарисовать равносторонний треугольник на листе бумаги или на доске. Чтобы нарисовать треугольник, нужно определить его размер и форму. Равносторонний треугольник имеет три равные стороны и углы, поэтому каждая сторона треугольника должна быть одинаковой длины.
Чтобы начать рисовать треугольник, возьмите линейку и карандаш. Начертите прямую линию на листе бумаги или на доске, которая будет являться одной из сторон треугольника.
Из конца этой линии, поставьте точку с помощью карандаша. Это будет вершина треугольника.
Поставьте конец линейки на эту точку и используйте уголки линейки, чтобы нарисовать еще две линии, исходящие из этой точки. Обе линии должны быть одной и той же длины, чтобы образовать равносторонний треугольник.
После того, как вы провели все три линии, вы должны получить равносторонний треугольник.
Шаг 2: Найти середину одной из сторон
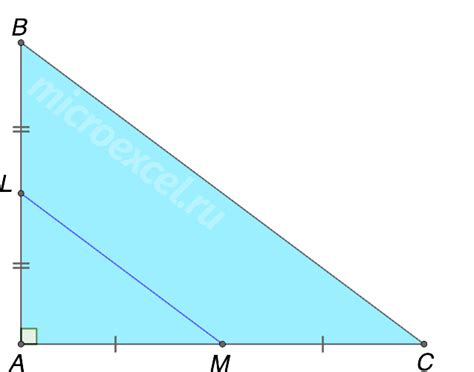
Для поиска медианы равностороннего треугольника необходимо найти середину одной из его сторон. Поскольку все стороны равны, середина одной из сторон будет также являться серединой треугольника.
Чтобы найти середину стороны, нужно измерить длину этой стороны и разделить ее пополам. Например, если длина стороны треугольника равна 10 единицам, то середина этой стороны будет находиться на расстоянии 5 единиц от одного из концов стороны.
Таким образом, проведите прямую линию, которая будет проходить через середину стороны и противоположный угол треугольника. Эта прямая линия является первой медианой равностороннего треугольника.
Шаг 3: Провести прямую линию от вершины до середины
На этом шаге мы будем проводить прямую линию от вершины треугольника до его середины.
Для начала, найдем середину стороны треугольника. Чтобы это сделать, применим следующую формулу:
Середина = (x1 + x2) / 2, (y1 + y2) / 2
Где x1 и y1 - координаты вершины треугольника, а x2 и y2 - координаты его середины.
Когда мы найдем середину стороны, проведем прямую линию от вершины треугольника до этой середины. Вы можете использовать линейку или наглухую карандаш для этого.
Важно, чтобы прямая линия проходила через вершину и середину стороны треугольника.
После того, как вы провели прямую линию, она должна разделить треугольник на две равные части. Теперь у вас есть два равных треугольника.
Продолжайте к следующему шагу, чтобы найти медиану равностороннего треугольника.
Расчет медианы равностороннего треугольника
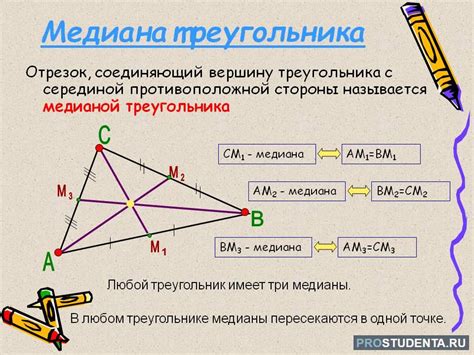
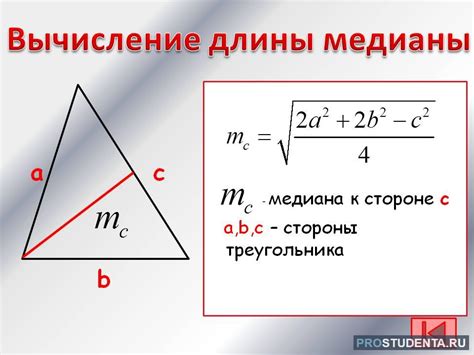
Для расчета медианы равностороннего треугольника, необходимо знать длину его стороны. Пусть сторона треугольника равна a. Тогда длина медианы может быть рассчитана по формуле:
M = (a * √3) / 2
Где M - длина медианы равностороннего треугольника.
Таким образом, для расчета медианы равностороннего треугольника, необходимо умножить длину его стороны на квадратный корень из трех и разделить полученное значение на 2.
| Сторона треугольника (a) | Длина медианы (M) |
|---|---|
| 1 | 0.866 |
| 2 | 1.732 |
| 3 | 2.598 |
| 4 | 3.464 |
Таким образом, длина медианы равностороннего треугольника увеличивается пропорционально длине его стороны. Расчет медианы может быть полезным при решении различных геометрических задач или при построении треугольника по заданным условиям.