Медиана - это числовое значение, которое делит упорядоченный набор данных на две половины. Она является одним из статистических показателей, характеризующих среднее значение в распределении случайной величины. Но что делать, если мы знаем только моду случайной величины и хотим найти ее медиану?
Мода - это значение, которое встречается наиболее часто в наборе данных. Зная моду, мы можем сделать предположение о форме распределения случайной величины. Но в отличие от среднего значения, мода не всегда может быть использована для определения медианы непосредственно.
Для того чтобы найти медиану случайной величины с известной модой, нам необходимо учесть следующие шаги. Во-первых, нужно определить, какая именно форма распределения случайной величины предполагается. Если мы имеем дело с нормальным распределением, то медиана будет совпадать с модой и средним значением. Однако, если распределение не является нормальным, то поиск медианы становится более сложной задачей.
Методы определения медианы случайной величины

Существует несколько методов определения медианы случайной величины:
1. Метод геометрической интерпретации. Этот метод основывается на графическом представлении функции распределения случайной величины. Медиана соответствует точке на графике функции распределения, где она пересекает линию координаты 0,5.
2. Метод половинных сумм. Этот метод заключается в упорядочивании значений случайной величины по возрастанию и нахождении среднего арифметического двух средних значений: среднего между двумя соседними значениями, которые окружают медиану.
3. Метод половинных долей. В этом методе необходимо упорядочить значения случайной величины по возрастанию и находить медиану как значение, которое делит выборку на две равные доли.
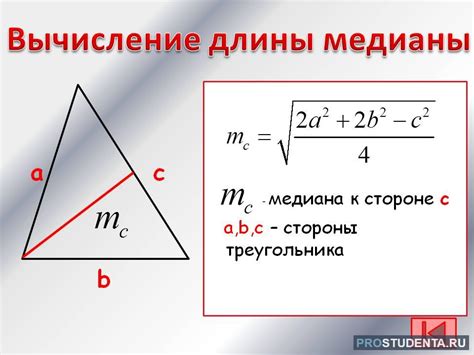
4. Метод формулы медианы для дискретных величин. В случае дискретной случайной величины медиану можно найти с помощью формулы: Медиана = X[n/2], где X[n/2] – это значение случайной величины, находящееся посередине, где n – количество значений случайной величины.
5. Метод формулы медианы для непрерывных случайных величин. В случае непрерывной случайной величины медиана равна значению, при котором площадь под графиком функции плотности вероятности слева от этого значения равна площади под графиком функции плотности вероятности справа от этого значения.
Таким образом, существует несколько методов определения медианы случайной величины, и выбор метода зависит от типа распределения и доступной информации о величине.
Графический метод нахождения медианы
Процесс построения графика медианы начинается с определения диапазона значений переменной, которая может принимать значения на числовой оси. Затем, в зависимости от специфики задачи, следует определить шаг изменения значений на оси и построить шкалу.
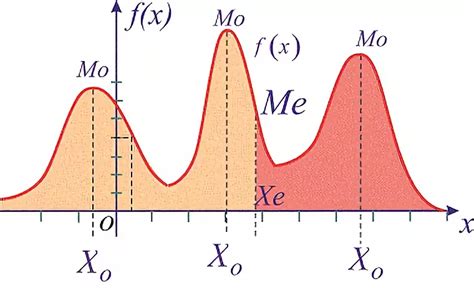
Далее, на графике необходимо отметить значение моды - наиболее часто встречающегося значения случайной величины. Это позволяет визуализировать центральную точку распределения вероятностей.
На этом же графике следует отметить значение медианы. Для этого рассчитывается площадь под графиком вероятностей от левого края графика до значения моды и сравнивается с площадью от левого края графика до значения медианы. После соответствующих вычислений получается значение медианы.
Графический метод нахождения медианы позволяет наглядно представить распределение вероятностей и определить положение медианы относительно моды. Этот метод особенно полезен при работе с различными случайными величинами, в том числе в статистике, экономике, физике и других научных областях.
| Преимущества графического метода нахождения медианы: | Недостатки графического метода нахождения медианы: |
|---|---|
| Наглядность и понятность визуализации данных | Требуется построение графика |
| Быстрота получения результата | Субъективность при определении положения медианы на графике |
| Возможность сравнения медианы с другими значениями | Требует достаточного количества данных для построения графика |
Вычислительная формула для определения медианы
Для вычисления медианы случайной величины с известной модой можно использовать следующую вычислительную формулу:
Медиана = мода - (3 * СрЗн / 2),
где мода - значение величины, которое наиболее часто встречается, СрЗн - среднее значение случайной величины.
Вычисление медианы позволяет получить представление о центральном значении набора данных и применяется в различных областях, включая статистику, экономику, медицину и другие сферы, где важно определить типичное значение случайной величины.
Пример нахождения медианы случайной величины с известной модой
Для начала, определимся с тем, что такое мода и медиана. Мода - это значение, которое наиболее часто встречается в выборке. Медиана - это значение, которое разделяет выборку на две равные части: половину значений больше медианы и половину значений меньше медианы.
Итак, у нас есть случайная величина X с известной модой. Чтобы найти медиану, мы можем использовать следующий подход:
- Найдем вероятность P(M) для значения моды M. Возможно, что это значение уже известно, например, если случайная величина имеет равномерное распределение, то вероятность любого значения в выборке будет одинакова.
- Разделим оставшуюся выборку на две группы: значения, меньшие моды, и значения, большие моды.
- Посчитаем сумму вероятностей значений, меньших моды, и найдем такое значение Ml, что сумма вероятностей значений, меньших Ml, равна 0.5 * P(M). Это значение будет левой границей медианы.
- Аналогично, найдем такое значение Mr, что сумма вероятностей значений, больших Mr, равна 0.5 * P(M). Это значение будет правой границей медианы.
- Медиана будет лежать между Ml и Mr, и мы можем принять ее как среднее значение этих границ.
Важно отметить, что в данном примере мы предполагаем, что вероятности значений меньше моды и больше моды равны (т.е. распределение симметрично относительно моды).
Пример: Допустим, у нас есть случайная величина X с модой M=5. Мы знаем, что вероятность P(M) для значения моды равна 0.2. Предположим также, что распределение симметрично относительно моды.
- Вероятность P(M) = 0.2.
- Оставшуюся выборку разделяем на значения, меньшие моды M=5, и значения, большие моды.
- Сумма вероятностей значений, меньших 5, должна быть равна 0.5 * 0.2 = 0.1. Найдем такое значение Ml, что сумма вероятностей значений, меньших Ml, равна 0.1.
- Аналогично, найдем значение Mr, такое что сумма вероятностей значений, больших 5, равна 0.1.
- Медиана будет лежать между Ml и Mr. Значение медианы можно принять как среднее значение этих границ.
Это лишь пример подхода к нахождению медианы случайной величины с известной модой. На практике могут использоваться и другие методы, в зависимости от распределения случайной величины и доступных данных.