Медиана – это среднее значение величины, которое отделяет верхнюю половину от нижней половины. В контексте статистики, медиана является одной из основных мер центральной тенденции случайной величины, представляющей собой статистическую характеристику, определяющую центральное значение выборки.
Медиана полезна в случаях, когда распределение данных не является симметричным или содержит выбросы. Она часто используется для анализа данных, особенно в экономике, социологии и здравоохранении. Применение медианы также распространено в математике, где она является одним из основных понятий статистики.
Процесс нахождения медианы величины х заключается в следующих шагах: сначала необходимо упорядочить данные по возрастанию, чтобы определить середину набора значений. Если количество значений элементов данных нечетно, то медиана будет являться значением, находящимся посередине. Если количество значений четно, то медиана будет представлять собой среднее арифметическое двух значений, находящихся посередине. Если данные не упорядочены, первым шагом будет их сортировка.
Что такое медиана?
Для нахождения медианы, упорядочите выборку по возрастанию или убыванию и найдите значение, которое находится посередине. Если количество значений в выборке нечетное, то медианой будет значение, которое находится точно посередине. Если количество значений четное, то медианой будет среднее арифметическое двух значений, находящихся посередине.
Медиана имеет ряд преимуществ по сравнению с другими мерами центральной тенденции, например, средним арифметическим.
Преимущества медианы:
- Устойчивость к выбросам. Медиана менее чувствительна к аномальным значениям, которые иногда встречаются в выборке.
- Не требует предположений о распределении данных. Медиана можно использовать как для симметричных, так и для асимметричных распределений.
- Ясное и наглядное представление о центральном значении выборки.
Медиана является одной из основных характеристик выборки, широко используемой в статистике и анализе данных.
Медиана случайной величины х
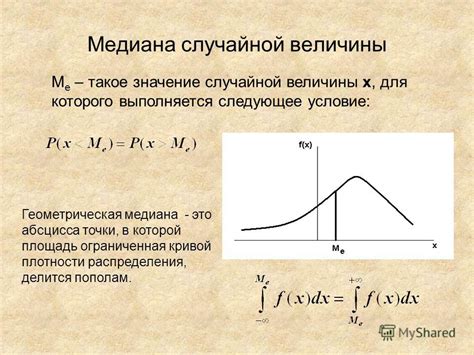
Чтобы найти медиану случайной величины х, необходимо следующие шаги:
- Упорядочить выборку значений случайной величины х по возрастанию.
- Если количество значений в выборке нечетное, медиана будет равна значению в середине упорядоченной выборки.
- Если количество значений в выборке четное, медиана будет равна среднему арифметическому двух значений в середине упорядоченной выборки.
Пример:
Рассмотрим следующий набор данных: 5, 1, 7, 2, 4, 5, 8, 3.
Упорядочивая этот набор данных по возрастанию, получаем: 1, 2, 3, 4, 5, 5, 7, 8.
Поскольку количество значений в выборке равно 8 (четное число), медиана будет равна среднему арифметическому двух значений в середине упорядоченной выборки, то есть (4 + 5) / 2 = 4.5.
В данном случае медиана равна 4.5, что означает, что 50% значений случайной величины х будут меньше или равны 4.5, а остальные 50% будут больше или равны 4.5.
Объяснение медианы в статистике

Для вычисления медианы необходимо упорядочить выборку в порядке возрастания или убывания и найти серединное значение. Если выборка имеет нечетное количество значений, то медианой будет значение точно посередине. Если выборка имеет четное количество значений, то медиана будет равна среднему арифметическому двух средних значений.
Пример:
| Вариант | Количество |
|---|---|
| 1 | 4 |
| 2 | 6 |
| 3 | 8 |
| 4 | 10 |
| 5 | 11 |
| 6 | 12 |
| 7 | 15 |
В данном примере выборка имеет семь значений. Чтобы найти медиану, необходимо упорядочить выборку: 1, 2, 3, 4, 5, 6, 7. Так как выборка имеет нечетное количество значений, медианой будет значение №4, то есть 10.
Медиана обладает важным свойством: она не чувствительна к выбросам в данных, в отличие от среднего значения. Это делает медиану полезной мерой для описания данных, особенно когда есть наличие выбросов или аномальных значений.
Как найти медиану?
| 1. Упорядочить набор данных по возрастанию. |
| 2. Если количество данных нечетное, то медиана будет значение в середине упорядоченного списка. Найдите значение, которое находится посередине. |
| 3. Если количество данных четное, то медиана будет средним арифметическим двух значений, которые находятся посередине упорядоченного списка. Найдите два значения, которые находятся посередине, и возьмите их среднее арифметическое. |
Рассмотрим пример. Пусть у нас есть набор данных: 2, 4, 6, 8, 10. Шаги для нахождения медианы будут следующими:
- Упорядочим данные в возрастающем порядке: 2, 4, 6, 8, 10.
- В данном случае количество данных нечетное, так что медианой будет значение 6, которое находится посередине.
Таким образом, медиана случайной величины х в данном примере равна 6.
Шаги по нахождению медианы

- Упорядочите значения: Начните с упорядочивания всех значений случайной величины от наименьшего к наибольшему. Если количество значений нечетное, выберите значение в середине упорядоченного списка.
- Найдите середину: Если количество значений четное, найдите два значения в середине упорядоченного списка. Затем найдите их среднее арифметическое для получения медианы.
- Запишите медиану: Запишите найденное значение как медиану случайной величины.
- Проверьте результат: Проведите проверку, убедившись, что выбранная медиана действительно соответствует упорядоченному списку значений. Если результат не верен, осмотритесь на предмет ошибок в процессе нахождения или перепроверьте значения.
Пример:
Пусть у нас есть следующие значения случайной величины: 2, 5, 1, 6, 3, 4. Следуя шагам, мы упорядочим значения: 1, 2, 3, 4, 5, 6. Количество значений - четное, поэтому нам нужно найти два значения в середине списка - 3 и 4. Среднее арифметическое этих двух значений равно 3.5. Таким образом, медиана этой случайной величины равна 3.5.
Примеры расчета медианы

Рассмотрим несколько примеров для лучшего понимания расчета медианы.
Пример 1:
Предположим, у нас есть следующий набор данных: 2, 4, 6, 8, 10. Для расчета медианы, мы сначала упорядочиваем данные в порядке возрастания: 2, 4, 6, 8, 10. В данном случае, у нас нечетное количество элементов, поэтому медиана будет являться элементом посередине, который равен 6.
Пример 2:
Предположим, у нас есть следующий набор данных: 1, 3, 5, 7. Упорядочиваем данные в порядке возрастания: 1, 3, 5, 7. В данном случае, у нас четное количество элементов, поэтому медиана будет вычисляться как среднее арифметическое двух элементов посередине, т.е. (3 + 5) / 2 = 4.
Пример 3:
Предположим, у нас есть следующий набор данных: 2, 4, 6, 8, 10, 12. Упорядочиваем данные в порядке возрастания: 2, 4, 6, 8, 10, 12. В данном случае, у нас четное количество элементов, поэтому медиана будет вычисляться как среднее арифметическое двух элементов посередине, т.е. (6 + 8) / 2 = 7.
Таким образом, расчет медианы позволяет нам определить центральное значение набора данных и является полезным инструментом в статистике и анализе данных.
Значение медианы

Медиана имеет важное значение в статистике, так как она представляет собой центральную точку или середину распределения данных. Значение медианы часто используется для описания среднего значения и для сравнения различных наборов данных.
В некоторых случаях медиана может быть более предпочтительным показателем центральной тенденции, чем среднее значение, особенно когда данные содержат выбросы или имеют асимметричное распределение. Медиана устойчива к экстремальным значениям, и не изменится при добавлении или удалении значений в наборе данных, если это не влияет на его упорядоченность.
Например, рассмотрим следующий набор данных: 5, 9, 15, 20, 25. Чтобы найти медиану, сначала упорядочим данные по возрастанию: 5, 9, 15, 20, 25. Затем найдем значение, которое разделяет набор данных на две равные части. В данном случае, медиана равна 15, так как она разделяет набор данных на две группы 5, 9, 15 и 20, 25.
Применение медианы в практике

Медиана, как показатель центральной тенденции, имеет широкое применение в различных областях практики. Вот некоторые примеры использования медианы:
- В медицине: медиана часто используется для анализа данных о заболеваниях и пациентах. Например, медианное время выздоровления после операции может быть полезным показателем для оценки эффективности лечения.
- В экономике: медиана может применяться для анализа доходов или расходов населения. Она позволяет получить представление о среднем уровне жизни людей, учитывая возможные выбросы или необычные значения в данных.
- В социологии и психологии: медиана может использоваться для изучения распределения определенных характеристик в группе людей. Например, медианное значение возраста может помочь определить типичный возрастной состав определенного общества.
- В географии: медиана может быть полезна для анализа данных о населении или климате различных регионов. Например, медианное значение температуры может помочь определить климатические особенности данной местности.
- В управлении проектами: медиана может использоваться для анализа времени выполнения определенных задач или этапов проекта. Это позволяет идентифицировать ключевые точки, где необходимо сосредоточить усилия или пересмотреть планы.
Сравнение медианы с другими показателями

Однако медиана не является единственным показателем центральной тенденции. Наиболее распространенными альтернативами являются среднее арифметическое и мода.
Среднее арифметическое - это сумма всех значений наблюдений, деленная на их количество. Этот показатель очень чувствителен к выбросам в данных, что может привести к смещению результата. В отличие от среднего, медиана устойчива к выбросам и дает более репрезентативное представление о данных.
Мода - это самое частое значение в выборке. Она может быть полезна для определения наиболее типичного значения случайной величины. Однако мода может быть неоднозначной, особенно в случае, если есть несколько значений с одинаковой частотой. В отличие от моды, медиана всегда является одним и единственным значением в выборке.
Сравнивая медиану с другими показателями, можно увидеть, что медиана более надежно отражает центральную тенденцию данных, особенно в случаях, когда выборка содержит выбросы или несимметрична. Поэтому медиана является важным инструментом при анализе статистических данных и принятии решений на их основе.