В геометрии медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Однако, что делать в случае, когда дана только одна сторона треугольника и ее высота? В этой статье мы рассмотрим простой метод нахождения медианы треугольника без гипотенузы и рассмотрим несколько примеров, чтобы лучше понять принцип работы данного метода.

Для начала давайте вспомним определение медианы треугольника. Как уже упоминалось, медиана - это отрезок, который соединяет вершину треугольника с серединой противоположной стороны. Однако, нам дана только одна сторона треугольника и ее высота, и у нас нет информации о других сторонах треугольника.

Для того чтобы найти медиану треугольника без гипотенузы, мы можем использовать простой метод, основанный на пропорциях. Нам необходимо знать высоту треугольника и его одну сторону. С помощью формулы геометрического места построения медианы, мы можем найти необходимую длину медианы треугольника без гипотенузы. Этот метод точен и может быть легко применен в практике.

Как найти медиану треугольника без гипотенузы

Для решения этой задачи, мы можем использовать свойство медианы, согласно которому медиана делит сторону треугольника на две равные половины.

Для нахождения медианы без гипотенузы, нужно провести две медианы, и точкой их пересечения найдется точка, которая будет являться серединой третьей стороны. Затем, проведем от этой точки прямую линию до вершины треугольника, у которой медианы не были проведены. Полученная линия будет являться медианой треугольника.

Пример:

Пусть у нас есть треугольник ABC, где AB = 8, AC = 10 и BC = 6. Мы должны найти медиану, исходящую из вершины B.

Шаг 1: Найдите середины сторон AC и BC. Пусть это будут точки M и N соответственно.

В нашем примере, точки M и N будут "6 см" и "5 см" от точки A и C соответственно.

Шаг 2: Проведите линию MN. Точка их пересечения будет точкой P, которая является серединой стороны AC.

Шаг 3: Проведите линию BP. Эта линия будет являться медианой треугольника.

Таким образом, мы можем найти медиану треугольника без гипотенузы, используя простой метод с использованием свойств медианы и серединных перпендикуляров.

Что такое медиана треугольника

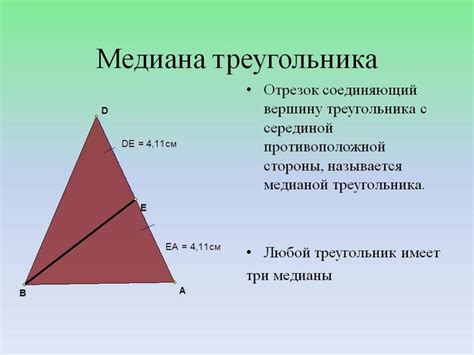
Медианы являются важной частью геометрии треугольника и имеют множество интересных свойств и применений. Они могут быть использованы для нахождения центра тяжести треугольника, а также для определения длин сторон и высот треугольника.

Медианы треугольника пересекаются в одной точке, называемой центром медиан. Этот центр является также центром тяжести треугольника и делит каждую медиану в отношении 2:1.

Медианы треугольника могут быть использованы для нахождения площади треугольника по формуле: S = (3/4) * √(s * (s - a) * (s - b) * (s - c)), где S - площадь треугольника, s - полупериметр треугольника, a, b, c - стороны треугольника.

Простой метод нахождения медианы

Простой метод нахождения медианы треугольника без гипотенузы состоит из нескольких шагов:

1. Найдите середину одной из сторон треугольника. Для этого разделите сторону пополам, соединив концы стороны отрезком.
2. Проведите отрезок, соединяющий вершину треугольника с найденной серединой. Этот отрезок будет являться медианой треугольника.

Применим этот метод на примере. Пусть у нас есть треугольник ABC, где AB = 6, BC = 8 и AC = 10.

Найдем медиану, проведенную из вершины A. Сначала найдем середину отрезка BC, который равен (8 + 10) / 2 = 9. Затем проведем медиану AM, соединяющую вершину A с серединой отрезка BC.

Таким образом, медиана треугольника АМ является отрезком AB, длина которого равна 6,5. Это значение можно использовать при решении задачи, например, для нахождения площади треугольника или его высоты.

Примеры и объяснение

Для наглядности, рассмотрим несколько примеров, чтобы лучше понять, как найти медиану треугольника без гипотенузы.

1. Пример 1:

   • Известно, что длины боковых сторон треугольника равны 8 и 12.
   • Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
   • Сначала найдем половину длины базы треугольника, то есть половину от 8, что равно 4.
   • Затем найдем половину длины боковой стороны, равную 6.
   • Теперь найдем длину медианы, применив теорему Пифагора: медиана в квадрате равна сумме квадратов половин базы и половин боковой стороны. То есть, медиана в квадрате равна 4^2 + 6^2 = 16 + 36 = 52. Извлекая корень из 52, получим приближенную длину медианы – 7.21.

2. Пример 2:

   • Длины боковых сторон треугольника равны 5 и 9.
   • Половина длины базы равна 4.
   • Половина длины боковой стороны равна 4.5.
   • Медиана в квадрате равна 4^2 + 4.5^2 = 16 + 20.25 = 36.25. Извлекая корень из 36.25, получим приближенную длину медианы – 6.01.

Вот таким простым способом мы можем находить медиану треугольника без гипотенузы. Важно помнить, что медиана разбивает отрезок, соединяющий вершину треугольника с серединой противоположной стороны, пополам. Это помогает нам упростить задачу и найти длину медианы с помощью теоремы Пифагора.