Медиана - это линия, которая соединяет вершину треугольника с серединой противоположной стороны. По сути, это отрезок, который делит сторону треугольника пополам.
Найти медиану треугольника из вершины - это важная задача в геометрии. Она может быть полезна для решения различных задач, например, для нахождения центра тяжести треугольника или построения окружности, касающейся сторон треугольника.
Для нахождения медианы треугольника из вершины нужно выполнить несколько шагов. Во-первых, найдите середину противоположной стороны. Это можно сделать, разделив длину стороны пополам. Во-вторых, соедините вершину треугольника с найденной серединой с помощью прямой линии. Получившаяся линия и будет медианой треугольника из вершины.
Важно отметить, что в треугольнике всегда есть три медианы, и они всегда пересекаются в одной точке. Эта точка называется центром тяжести треугольника и обозначается буквой G. Она делит каждую медиану в отношении 2:1, то есть отрезок от вершины треугольника до центра тяжести в два раза короче, чем от вершины треугольника до середины противоположной стороны.
Что такое медиана треугольника?
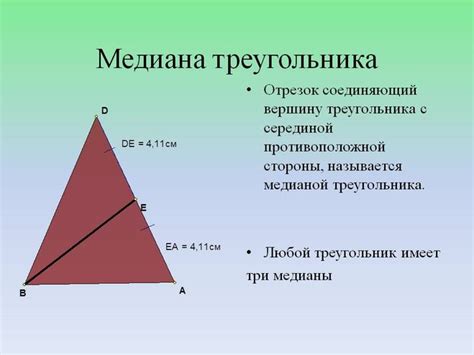
Медианы треугольника пересекаются в одной точке, называемой центром тяжести или барицентром треугольника. Барицентр является точкой баланса треугольника, и если повесить сам треугольник на вершину барицентра, он будет равномерно распределен по всем сторонам.
Медианы треугольника имеют несколько интересных свойств. Во-первых, они делятся барицентром в отношении 2:1, то есть расстояние от вершины до барицентра в два раза больше, чем расстояние от барицентра до середины противолежащей стороны.
Во-вторых, медианы равны по длине, что значит, что каждая медиана делит площадь треугольника на две равные части.
Медианы треугольника имеют большое практическое значение. Они используются, например, для нахождения центра тяжести различных объектов и конструкций. Изучение медиан треугольника помогает лучше понять его геометрию и свойства.
Определение и основные свойства

Основные свойства медианы треугольника из вершины:
- Все медианы пересекаются в одной точке, называемой центром тяжести или барицентром треугольника.
- Медиана делит соответствующую сторону пополам, то есть, отношение длины сегмента стороны к длине всей стороны равно 1/2.
- Медиана является биссектрисой угла при вершине треугольника, которая делит этот угол пополам.
- Центр тяжести треугольника, точка пересечения медиан, располагается на две трети от высоты, проведенной из вершины до противоположной стороны.
- Медианы являются отрезками, которые обладают наименьшей длиной по сравнению с другими сегментами, соединяющими вершины треугольника со стороной.
Как найти медиану треугольника из вершины?
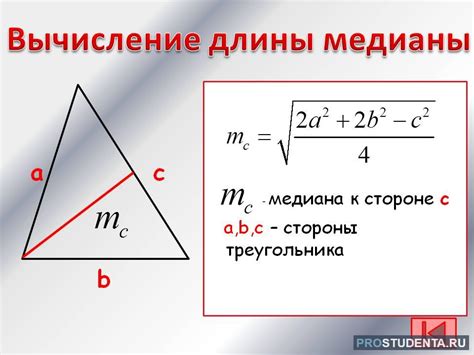
Для того чтобы найти медиану треугольника, вам понадобится знать координаты вершины треугольника и координаты середины противоположной стороны.
Шаги по нахождению медианы треугольника из вершины:
- Определите координаты вершины треугольника.
- Определите координаты середины противоположной стороны. Для этого найдите среднюю точку противоположной стороны треугольника.
- Используя найденные координаты, вычислите разность координат вершины треугольника и середины противоположной стороны.
- Разделите полученную разность на два, чтобы найти середину медианы треугольника. Для этого умножьте каждую координату разности на 0.5.
- Сложите полученные координаты середины медианы с координатами вершины треугольника, чтобы найти координаты конечной точки медианы.
Когда вы найдете координаты конечной точки медианы, вы сможете визуализировать ее на графике или использовать для дальнейших вычислений.
Обратите внимание, что данный метод работает только для треугольников, у которых все вершины имеют разные координаты. Если у треугольника есть вершины с одинаковыми координатами, то найденная медиана будет некорректна.
Надеемся, что данное руководство поможет вам находить медиану треугольника из его вершины.
Шаг 1: Найдите середину противоположной стороны

Перед тем как найти медиану треугольника, вам нужно найти середину противоположной стороны. Чтобы это сделать, выполните следующие действия:
| Шаг | Описание |
|---|---|
| 1 | Нарисуйте треугольник и обозначьте его три вершины: A, B и C. |
| 2 | Выберите любую из сторон треугольника и назовите ее AB. |
| 3 | Используя линейку, измерьте длину стороны AB и разделите ее пополам. Это будет точка D. |
| 4 | На стороне AB, укажите точку D, образовавшуюся после разделения пополам. |
Теперь вы нашли середину противоположной стороны треугольника. Вы можете использовать эту точку для дальнейших вычислений, чтобы найти медиану треугольника.
Шаг 2: Проведите от середины противоположной стороны медиану

Для проведения медианы, найдите середину противоположной стороны треугольника и пометьте ее. Затем, используя линейку или другой подходящий инструмент, проведите прямую линию от данной середины до противоположной вершины треугольника.
Шаг 2: Проведите от середины противоположной стороны медиану |
Убедитесь, что линия проходит через середину противоположной стороны треугольника и достигает противоположной вершины. Эта проведенная линия является второй медианой треугольника из данной вершины и помогает определить его медиану.
После проведения линий медианы второй вершины треугольника, вы можете перейти к следующему шагу, прежде чем окончательно определить медиану треугольника из данной вершины.
Шаг 3: Найдите точку пересечения медианы и противоположной стороны
После нахождения середин каждой стороны треугольника, мы можем перейти к поиску точки пересечения медианы и противоположной стороны. Эта точка называется центром тяжести треугольника и обозначается как G.
Чтобы найти центр тяжести, соедините медиану, проходящую через вершину V, с серединой противоположной стороны. Получившаяся линия пересечется с прямой, содержащей противоположную сторону, в точке G.
Точка G является центром массы треугольника, и находится на одной третьей расстояния от каждой вершины.
Итак, для нахождения точки G, мы можем использовать следующий алгоритм:
- Найдите середину каждой стороны треугольника.
- Проведите медиану, проходящую через вершину треугольника и середину противоположной стороны.
- Эта медиана пересекается с противоположной стороной в точке G, которая является центром тяжести треугольника.
Теперь у вас есть все необходимые инструкции для нахождения точки пересечения медианы и противоположной стороны треугольника. Продолжайте следовать этим шагам для решения данной задачи.
Зачем нужно знать, как найти медиану треугольника?

Во-первых, знание о медианах позволяет нам лучше понять треугольник в целом. Медианы разбивают треугольник на шесть равных треугольников, что помогает нам анализировать его свойства и проводить различные доказательства.
Во-вторых, медианы могут быть использованы для нахождения центра тяжести треугольника. Центр тяжести - это точка пересечения трех медиан, и он является центральным и важным понятием в геометрии. Знание о медианах позволяет нам легко определить и найти центр тяжести треугольника.
Наконец, медианы треугольника имеют также важное практическое значение. Они могут быть использованы, например, для построения перпендикуляров к сторонам треугольника или для нахождения высоты треугольника. Знание о медианах позволяет нам решать разнообразные задачи, связанные с треугольниками и их свойствами.
Таким образом, понимание, как найти медиану треугольника, является важным для развития навыков аналитического мышления, геометрического анализа и решения различных задач на плоскости. Это навык, который может быть полезен не только в математике, но и в других областях, требующих логического и геометрического мышления.
Применение в геометрии и решении задач

Применение медианы треугольника имеет важное значение в различных областях геометрии, включая:
- Наложение форм: Медианы треугольника используются для наложения, трансформации и выравнивания форм. Они позволяют рассчитывать позицию и размер объектов на плоскости.
- Нахождение центра тяжести: Медианы треугольника помогают определить его центр тяжести (центр масс), который является точкой, где сумма моментов сил относительно данной точки равна нулю.
- Решение геометрических задач: Медианы треугольника используются для решения различных геометрических задач, таких как определение площади треугольника или построение других геометрических фигур.
- Расчет пересечений: Медианы треугольника используются для определения точек пересечения с другими линиями или фигурами.
Важно помнить, что медиана треугольника из вершины имеет особую геометрическую характеристику - она проходит через точку, которая делит ее в отношении 2:1. Это означает, что от вершины до середины противоположной стороны расстояние в два раза больше, чем от вершины до точки пересечения с медианой.
Примеры нахождения медианы треугольника

Рассмотрим несколько примеров, чтобы лучше понять, как найти медиану треугольника из вершины.
Пример 1:
Дан треугольник ABC, в котором:
- Вершина A с координатами (2, 4)
- Вершина B с координатами (6, 8)
- Вершина C с координатами (4, 2)
Чтобы найти медиану из вершины A, нужно:
- Найти середину отрезка BC, используя формулу:
- Провести прямую линию из вершины A в найденную середину отрезка BC. Это и будет медиана из вершины A.
x = (xB + xC) / 2
y = (yB + yC) / 2
Таким образом, середина отрезка BC будет иметь координаты:
x = (6 + 4) / 2 = 5
y = (8 + 2) / 2 = 5
Пример 2:
Дан треугольник XYZ, в котором:
- Вершина X с координатами (1, 3)
- Вершина Y с координатами (5, 7)
- Вершина Z с координатами (3, 1)
Чтобы найти медиану из вершины Z, нужно:
- Найти середину отрезка XY, используя формулу:
- Провести прямую линию из вершины Z в найденную середину отрезка XY. Это и будет медиана из вершины Z.
x = (xX + xY) / 2
y = (yX + yY) / 2
Таким образом, середина отрезка XY будет иметь координаты:
x = (1 + 5) / 2 = 3
y = (3 + 7) / 2 = 5
Таким образом, используя формулу нахождения середины отрезка, можно легко найти медиану треугольника из любой его вершины.
Пример 1: Медиана треугольника со сторонами 3, 4 и 5
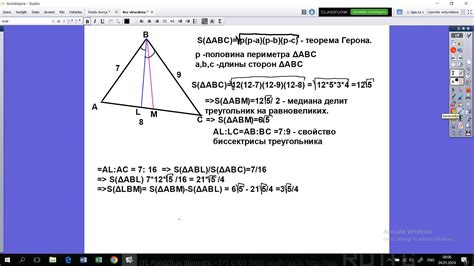
Дано треугольник со сторонами 3, 4 и 5. Найдем медиану треугольника, которая соединяет вершину с противолежащей стороной.
Для нахождения медианы, нужно разделить противолежащую сторону пополам. Найдем ее длину:
Противолежащая сторона треугольника имеет длину 5.
Длина медианы равна половине длины противолежащей стороны, поэтому:
Длина медианы = 5 / 2 = 2.5
Таким образом, медиана треугольника со сторонами 3, 4 и 5 равна 2.5.
