Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Нахождение медианы треугольника на координатной плоскости позволяет определить ее координаты и использовать их для проведения дальнейших расчетов и задач.
Для нахождения медианы треугольника на координатной плоскости необходимо знать координаты вершин треугольника. Обозначим эти вершины как точки A (x1, y1), B (x2, y2) и C (x3, y3). Сначала найдем середину отрезка AB путем нахождения среднего значения координат x и y: точка M ((x1 + x2) / 2, (y1 + y2) / 2).
Затем, найдем координаты медианы треугольника BG, соединяющей вершину B с серединой противоположной стороны AC. Координаты точки G равны средним значениям координат точек A и C: точка G ((x1 + x3) / 2, (y1 + y3) / 2).
Наконец, найдем координаты медианы треугольника CM, проведенной из вершины C к середине противоположной стороны AB. Координаты точки M можно найти аналогично середине отрезка AB: точка N ((x2 + x3) / 2, (y2 + y3) / 2).
Итак, мы нашли координаты всех трех медиан треугольника на координатной плоскости. Используя эти координаты, можно проводить дальнейшие геометрические и численные расчеты, а также решать задачи, связанные с треугольником.
Определение медианы треугольника
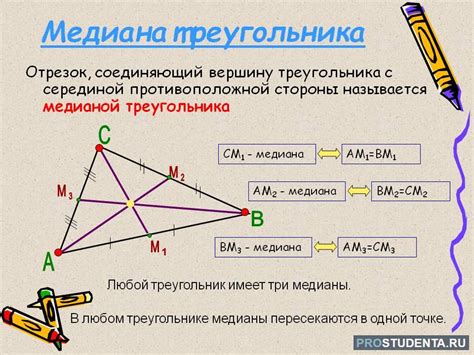
Медианы являются основными линиями треугольника и обладают несколькими интересными свойствами. Одно из главных свойств медиан заключается в том, что они пересекаются в одной точке, которая находится на расстоянии две трети от каждой вершины треугольника. Эта точка называется центром тяжести и является точкой баланса, в которой сосредоточена половина массы треугольника.
Медианы также помогают определить центр окружности, вписанной в треугольник. Центр окружности, пользующейся таким свойством, лежит на пересечении медиан и является точкой радикального центра треугольника. Это означает, что медианы являются важным инструментом для анализа и конструирования треугольников на координатной плоскости.
Определение медианы треугольника на координатной плоскости может быть осуществлено с использованием формул и правил алгебры. Зная координаты вершин треугольника, можно рассчитать координаты середины сторон, а затем задать уравнение прямой в виде y = kx + b, где k и b – это коэффициенты, которые можно вычислить по формулам. Полученные уравнения прямых будут представлять комбинацию уравнений медиан треугольника.
Таким образом, определение медианы треугольника является важным элементом геометрии на плоскости, позволяющим анализировать и конструировать треугольники с использованием алгебраических методов. Знание этого понятия поможет углубить понимание пространственной геометрии и применение математических приемов в различных ситуациях.
Что такое медиана треугольника и зачем она нужна
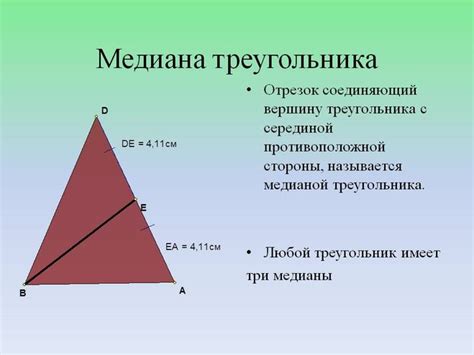
Медианы являются важным элементом треугольника и часто используются в геометрических задачах. Они позволяют нам находить различные параметры треугольника, такие как площадь, периметр, координаты центра тяжести и другие.
Одно из основных свойств медианы треугольника заключается в том, что все три медианы пересекаются в одной точке, которая называется центром тяжести треугольника. Центр тяжести является точкой баланса треугольника и имеет координаты, равные средним значениям координат вершин треугольника.
Зная координаты вершин треугольника, мы можем легко вычислить координаты точки пересечения медиан. Это можно сделать, используя формулу:
| Координата x | Координата y |
|---|---|
| (x1 + x2 + x3) / 3 | (y1 + y2 + y3) / 3 |
Таким образом, медианы треугольника позволяют нам находить его геометрические характеристики и использовать их в различных математических задачах.
Как найти координаты вершин треугольника

Если известны координаты трех точек треугольника, можно легко найти координаты его вершин. Например, если известны координаты точек A(x1, y1), B(x2, y2) и C(x3, y3), то координаты вершин треугольника будут следующими:
Вершина A: (x1, y1)
Вершина B: (x2, y2)
Вершина C: (x3, y3)
Таким образом, чтобы найти координаты вершин треугольника, достаточно знать координаты трех точек, образующих этот треугольник.
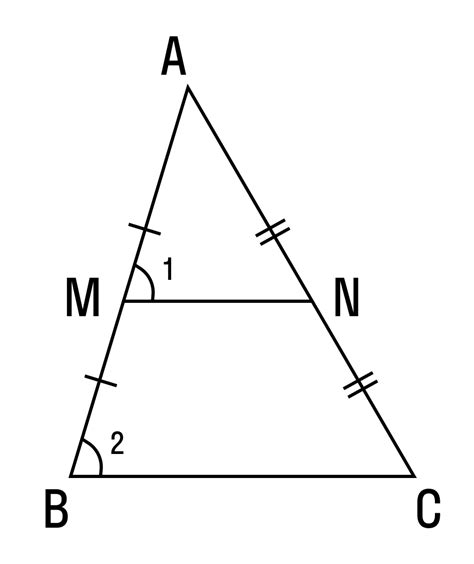
Как найти середины сторон треугольника
| Сторона треугольника | Координаты концов стороны | Формула для нахождения середины стороны |
|---|---|---|
| AB | (xA, yA) и (xB, yB) | ((xA + xB)/2, (yA + yB)/2) |
| BC | (xB, yB) и (xC, yC) | ((xB + xC)/2, (yB + yC)/2) |
| CA | (xC, yC) и (xA, yA) | ((xC + xA)/2, (yC + yA)/2) |
Используя эти формулы, мы можем легко найти середины каждой стороны треугольника, которые будут являться вершинами нового треугольника. Это позволит нам рассмотреть различные свойства треугольника и найти его медианы, площадь и другие параметры.
Как найти координаты точки пересечения медиан треугольника
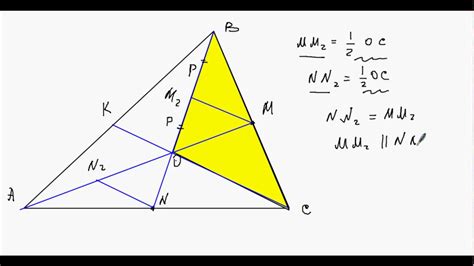
Для нахождения координат точки пересечения медиан нужно воспользоваться следующей формулой:
| Формула | Координаты медиан |
|---|---|
| x = (x1 + x2 + x3) / 3 | Координаты вершин треугольника: (x1, y1), (x2, y2), (x3, y3) |
| y = (y1 + y2 + y3) / 3 | Координаты центроиды: (x, y) |
Следуя этой формуле, найдите суммы координат вершин треугольника и разделите их на 3, чтобы получить координаты центроиды. Например, если координаты вершин треугольника равны: (x1, y1), (x2, y2), (x3, y3), то координаты центроиды будут равны:
x = (x1 + x2 + x3) / 3
y = (y1 + y2 + y3) / 3
Таким образом, вы найдете координаты точки пересечения медиан треугольника, которую также называют центроидой.