Треугольник – одна из простейших фигур в геометрии, имеющая три стороны и три угла. Расчет различных параметров треугольника может быть полезным в различных областях: от строительства до решения математических задач. В данной статье мы рассмотрим один из важных параметров треугольника – медиану, и расскажем о том, как ее найти по известным сторонам и площади треугольника.
Медиана треугольника – это отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны. Медианы пересекаются в одной точке – центре тяжести треугольника. Медианы являются важными элементами треугольника и используются для нахождения различных его характеристик.
Существует несколько способов найти медиану треугольника, но самыми распространенными являются методы, основанные на известных сторонах и площади треугольника. Для нахождения медианы по сторонам треугольника необходимо знать длины всех трех сторон. А для нахождения медианы по площади треугольника необходимо знать площадь и одну из сторон треугольника. В этой статье мы рассмотрим оба этих метода и дадим подробные инструкции по их применению.
Определение медианы треугольника: что это и для чего нужно знать
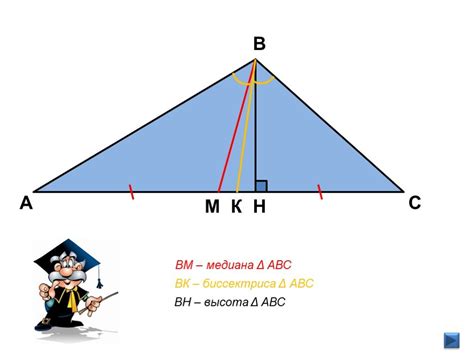
Определение медианы треугольника является важной частью изучения геометрии. Знание медиан позволяет лучше понять свойства треугольников и применять их при решении различных задач в физике, математике и других науках.
Изучение медианы треугольника может быть полезно для определения различных характеристик треугольника. Например, медианы могут помочь найти центр масс треугольника, который является точкой пересечения всех трех медиан. Также, медианы треугольника могут использоваться для поиска площади треугольника по формуле Герона.
Понимание медиан треугольника также помогает в изучении симметрии треугольника и его свойств. Например, медианы треугольника делятся в отношении 1:2, то есть, отрезок между вершиной и серединой стороны равен двум отрезкам между серединой этой стороны и другими двумя вершинами. Это свойство можно использовать при построении треугольников или расчете их геометрических размеров.
Таким образом, знание медиан треугольника позволяет более глубоко понять структуру и свойства треугольников, что является важным для различных областей науки и практического применения геометрии.
Как найти медиану треугольника по сторонам: подробная инструкция
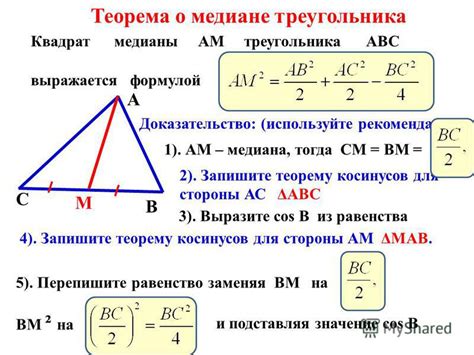
Чтобы найти медиану треугольника по сторонам, следуйте следующим шагам:
Шаг 1: Запишите значения длин сторон треугольника. Для примера, предположим, что стороны треугольника равны a, b и c.
Шаг 2: Используя формулу для нахождения длины медианы треугольника, вычислите длины всех трех медиан. Формула для нахождения длины медианы треугольника:
Медиана_a = (sqrt(2b^2 + 2c^2 - a^2)) / 2
Медиана_b = (sqrt(2a^2 + 2c^2 - b^2)) / 2
Медиана_c = (sqrt(2a^2 + 2b^2 - c^2)) / 2
Шаг 3: Рассчитайте значения медиан и запишите результаты. Вы получите три значения для каждой медианы.
Например, если стороны треугольника a = 5, b = 12 и c = 13, то значения медиан будут:
Медиана_a = (sqrt(2 * 12^2 + 2 * 13^2 - 5^2)) / 2 = 6.41
Медиана_b = (sqrt(2 * 5^2 + 2 * 13^2 - 12^2)) / 2 = 7.00
Медиана_c = (sqrt(2 * 5^2 + 2 * 12^2 - 13^2)) / 2 = 5.39
Таким образом, медианы треугольника равны 6.41, 7.00 и 5.39 соответственно.
Теперь вы знаете, как найти медиану треугольника по сторонам! Эта информация может быть полезна при решении различных задач геометрии.
Формула для вычисления медианы треугольника по площади: шаги и примеры
Для вычисления медианы треугольника по площади необходимо использовать следующую формулу:
| Медиана по площади (m) | = | 2/3 * (√(2 * сторона А2 + 2 * сторона В2 - сторона С2) / 2) |
| где сторона А, Б, С - длины сторон треугольника. | ||
Давайте рассмотрим пример вычисления медианы треугольника по площади:
У нас есть треугольник со сторонами A = 5, B = 7 и C = 8.
Сначала вычислим площадь треугольника по формуле Герона:
| p | = | (5 + 7 + 8) / 2 | = | 10 |
| Площадь (S) | = | √(10 * (10 - 5) * (10 - 7) * (10 - 8)) | = | √(10 * 5 * 3 * 2) | = | √300 | = | 17.32 |
Теперь вычислим медиану по площади:
| Медиана по площади (m) | = | 2/3 * (√(2 * 52 + 2 * 72 - 82) / 2) | = | 2/3 * (√(2 * 25 + 2 * 49 - 64) / 2) | = | 2/3 * (√(50 + 98 - 64) / 2) | = | 2/3 * (√84 / 2) | = | 2/3 * (9.17 / 2) | = | 6.11 |
Таким образом, медиана треугольника по площади равна 6.11.
Полезные советы по нахождению медианы треугольника
Вот несколько полезных советов, которые помогут вам находить медианы треугольника:
- Выберите сторону, по которой вы хотите найти медиану.
- Найдите середину этой стороны. Середина стороны - это точка, которая делит сторону на две равные части.
- Соедините вершину треугольника с найденной серединой стороны. Это и будет медиана, проходящая через данную сторону.
- Повторите те же шаги для остальных двух сторон треугольника, чтобы найти все три медианы.
- Если вам даны значения сторон треугольника, вы можете использовать формулу для нахождения длины медианы: M = 0.5 * sqrt(2 * (a^2 + b^2) - c^2), где M - длина медианы, a, b, c - длины сторон треугольника.
Знание медиан треугольника полезно при решении различных геометрических задач и нахождении центра тяжести треугольника. Надеемся, эти советы помогут вам легко и точно находить медианы треугольника.
Как применить медиану треугольника в реальной жизни
1. Строительство:
Медианы треугольников могут быть использованы при проектировании и строительстве зданий. Например, при застройке участка, где требуется размещение здания в определенном соответствии с окружающими объектами, медианные линии могут помочь определить оптимальное положение. Также применение медианы может быть полезно при расчете геометрических параметров здания, например, для определения центра масс.
2. География:
Медианы треугольников используются в географии при определении центра масс расположения различных объектов, таких как города, озера, или горы. Использование медианы позволяет учесть географическое положение объектов и определить их общий центр. Это может быть полезно при планировании инфраструктуры или при оценке географического распределения природных ресурсов.
3. Измерение:
Медианы треугольников также могут быть использованы для измерения расстояний и площадей. Например, в геодезии медианные линии используются для определения длин и высот различных географических объектов. Также медианы могут помочь визуально определить площадь поля или участка земли.
Ключевые отличия медианы от других величин треугольника
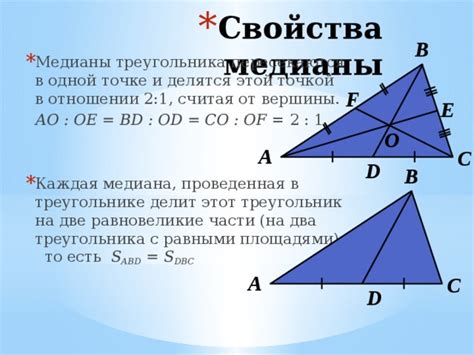
1. Противоположность сторонам: Медиана не является стороной треугольника, но соединяет вершину с противоположной стороной, делая ее уникальной и отличной от других величин.
2. Серединное положение: Медиана проходит через середину противоположной стороны, деля ее на две равные части. Это является ключевой особенностью медианы и отличает ее от биссектрисы и высоты треугольника.
3. Пересечение: Медианы треугольника пересекаются в точке, которую называют центром масс треугольника или точкой пересечения медиан. Это специальная точка, которая делит каждую медиану в отношении 2:1.
4. Роль в конструкции: Медианы треугольника используются при построении других важных элементов, таких как центр описанной окружности и центр вписанной окружности.
Изучение медиан треугольника помогает понять его особенности и свойства, а также отличить их от других величин, таких как биссектриса и высота. Медиана играет важную роль в геометрии и может быть использована для решения различных задач и конструкций.
Примеры вычисления медианы треугольника
Пример 1:
| Сторона AB | Сторона BC | Сторона CA | Площадь треугольника | Медиана треугольника |
|---|---|---|---|---|
| 5 | 6 | 7 | 9 | 4.5 |
Для треугольника со сторонами AB = 5, BC = 6 и CA = 7, и площадью треугольника равной 9, медиана треугольника равна 4.5.
Пример 2:
| Сторона AB | Сторона BC | Сторона CA | Площадь треугольника | Медиана треугольника |
|---|---|---|---|---|
| 3 | 4 | 5 | 6 | 3.5 |
Для треугольника со сторонами AB = 3, BC = 4 и CA = 5, и площадью треугольника равной 6, медиана треугольника равна 3.5.
Это всего лишь некоторые примеры вычисления медианы треугольника. Вы можете использовать эти примеры в своих вычислениях или следовать инструкциям, чтобы найти медиану треугольника по сторонам и площади.