Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Этот параметр играет важную роль в геометрии и позволяет нам определить некоторые характеристики треугольника. Нахождение медианы треугольника по заданным сторонам требует применения таких математических операций, как вычисление среднего значения и построение серединных перпендикуляров.
Для определения медианы треугольника, которая проходит через стороны a, b и c, мы можем использовать формулу:
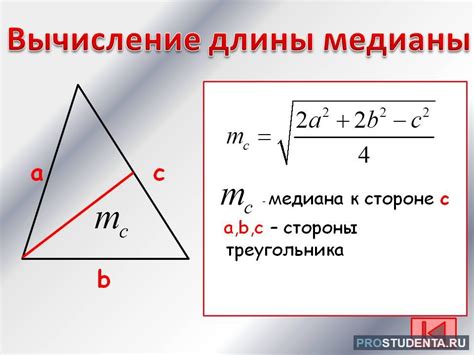
Медиана треугольника = √(2 * b^2 + 2 * c^2 - a^2) / 2
Где символ "^" обозначает возведение в степень. Отметим, что формула для нахождения медианы треугольника действительна только для треугольников, в которых длины сторон a, b и c удовлетворяют неравенству треугольника: a + b > c, a + c > b и b + c > a.
Теперь, когда у нас есть формула для нахождения медианы треугольника по его сторонам, мы можем приступить к вычислениям. Зная длины сторон треугольника, мы можем подставить их в формулу и получить конечный результат. Найденная медиана поможет нам определить геометрические особенности треугольника и использовать эти данные в различных задачах и вычислениях.
Что такое медиана треугольника
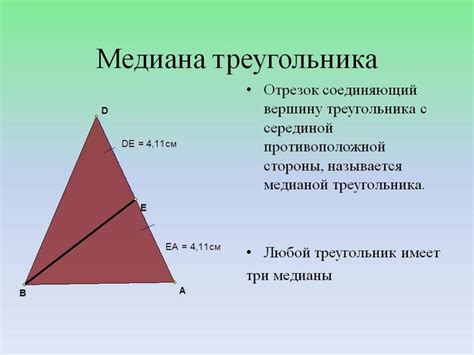
В каждом треугольнике есть три медианы - они соединяют вершины треугольника с серединами противоположных сторон. Точка пересечения всех трех медиан называется центром тяжести треугольника или барицентром.
Медианы треугольника имеют несколько важных свойств:
- Медианы треугольника равны по длине.
- Центр тяжести треугольника делит медианы в отношении 2:1. Это означает, что расстояние от вершины треугольника до центра тяжести вдвое больше, чем расстояние от центра тяжести до середины противоположной стороны.
- Медиана треугольника является линией симметрии для треугольника, она делит его на две равные части.
Медианы треугольника являются важной геометрической характеристикой и широко используются в решении задач и построении различных фигур.
Как найти медиану треугольника через площадь
Медиана = (2/3) * (√3/2) * сторона
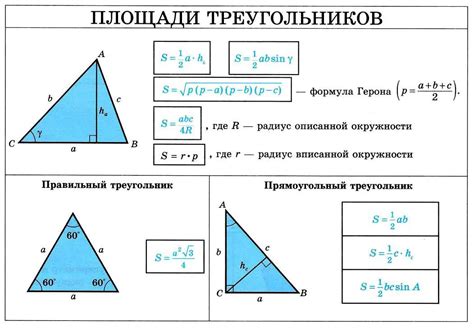
Для начала, рассчитаем площадь треугольника, используя формулу площади Герона:
Площадь = √(p * (p - a) * (p - b) * (p - c))
Где a, b и c - стороны треугольника, а p - полупериметр, вычисляемый по формуле:
p = (a + b + c) / 2
Зная площадь треугольника и длину стороны, мы можем вычислить медиану треугольника с помощью формулы:
Медиана = (2/3) * (√3/2) * √(p * (p - a) * (p - b) * (p - c))
Теперь у нас есть формула для нахождения медианы треугольника через площадь. Просто подставьте значения сторон треугольника и решите уравнение, чтобы найти медиану. Таким образом, вы можете точно найти медиану треугольника и использовать ее для различных математических или геометрических вычислений.
Как найти медиану треугольника через координаты вершин

Для нахождения медианы треугольника через координаты его вершин можно использовать следующие формулы:
| Вершина | Середина противоположной стороны |
|---|---|
| (x1, y1) | (x23 = (x2 + x3) / 2, y23 = (y2 + y3) / 2) |
| (x2, y2) | (x13 = (x1 + x3) / 2, y13 = (y1 + y3) / 2) |
| (x3, y3) | (x12 = (x1 + x2) / 2, y12 = (y1 + y2) / 2) |
Таким образом, чтобы найти координаты всех трех медиан треугольника, необходимо вычислить середины противоположных сторон. Полученные координаты представляют собой середины отрезков, которые являются медианами треугольника.
Зная координаты середин противоположных сторон, легко найти уравнения медиан треугольника и получить их уравнения в таком виде: y = kx + b.
Теперь вы можете использовать эти формулы для нахождения медиан треугольника, опираясь на координаты его вершин.
Пример вычисления медианы треугольника
Для вычисления медианы треугольника по его сторонам, сначала необходимо найти его площадь. После этого можно определить длины медиан, используя соотношения между длинами сторон и медианами треугольника.
Рассмотрим следующий пример:
| Сторона | Длина |
|---|---|
| AB | 5 |
| BC | 6 |
| CA | 7 |
Для начала, найдем площадь треугольника по формуле площадь = √p(p-AB)(p-BC)(p-CA), где p = (AB + BC + CA) / 2.
В нашем случае, p = (5 + 6 + 7) / 2 = 9.
Подставляя значения в формулу, получаем:
площадь = √9(9-5)(9-6)(9-7) = √9 * 4 * 3 * 2 = √(9 * 4 * 3 * 2) = √216 = 14.6969
Далее, для вычисления длин медиан треугольника, можно использовать следующие формулы:
Медиана, проведенная из вершины A, делит медиану, проведенную из противоположной вершины A, в отношении 2:1. Это означает, что длина медианы, проведенной из вершины A, будет равна (2/3) * длина медианы, проведенной из противоположной вершины A.
Аналогично для медиан, проведенных из вершин B и C.
Используя эти соотношения, можно вычислить длины медиан следующим образом:
Медиана из вершины A: (2/3) * 14.6969 = 9.7979
Медиана из вершины B: (2/3) * 14.6969 = 9.7979
Медиана из вершины C: (2/3) * 14.6969 = 9.7979
Таким образом, длины медиан треугольника, проведенных из вершин A, B и C, соответственно, равны 9.7979.
Именно таким образом можно вычислить медиану треугольника по его сторонам.
Медиана треугольника как ось симметрии
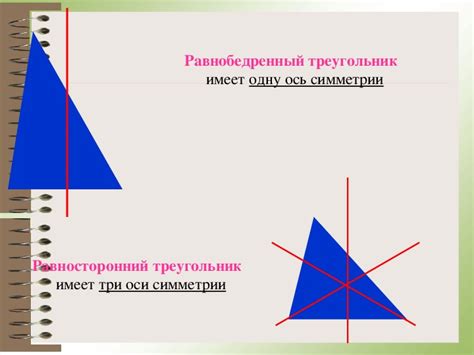
Ось симметрии – это линия, которая делит фигуру на две части, симметричные относительно этой линии. Ось симметрии может быть вертикальной, горизонтальной или диагональной. В случае медианы треугольника, она является главной (главной осью симметрии).
Имея медиану в треугольнике, можно утверждать, что треугольник симметричен относительно его. Если отразить треугольник относительно медианы, получится его точная копия.
Медианы треугольника пересекаются в одной точке, которая называется центром тяжести или барицентром. Этот центр тяжести делит медианы в соотношении 2:1, то есть медиана, соединяющая вершину с центром тяжести, в два раза длиннее медианы, соединяющей середину противолежащей стороны с центром тяжести.
Свойства медиан треугольника
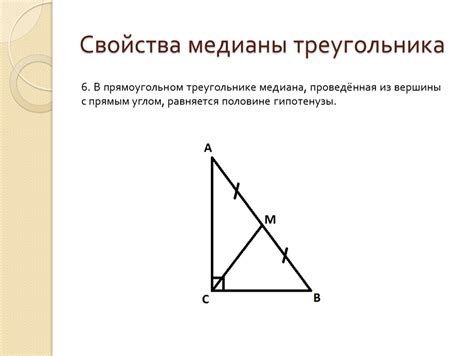
1. Точка пересечения медиан
Пересечение медиан треугольника называется центром масс. Эта точка делит медианы в отношении 2:1. То есть, если обозначить середины сторон треугольника как A', B' и C', а точку пересечения медиан как G, то G делит каждую медиану в отношении AG:GA' = BG:GB' = CG:GC'.
2. Равенство площадей треугольников
Медианы делят треугольник на шесть меньших треугольников. Площадь каждого из этих треугольников равна четверти площади исходного треугольника. То есть, сумма площадей трех треугольников, образованных медианами, равна половине площади всего треугольника.
3. Связь с другими линиями треугольника
Медианы треугольника также связаны с другими важными линиями треугольника, такими как высоты и биссектрисы. Например, точки пересечения медиан с высотами и биссектрисами треугольника делят их в определенных отношениях.
Эти свойства медиан треугольника позволяют решать различные задачи, связанные с треугольниками, и являются важным инструментом в геометрии.