Медиана треугольника – это отрезок, соединяющий один вершину треугольника с серединой противоположной стороны. Вычисление медианы треугольника может быть полезным для решения различных геометрических задач и нахождения центра масс треугольника.
Одним из способов нахождения медианы треугольника является использование теоремы косинусов. Согласно этой теореме, косинус угла треугольника равен отношению квадрата длины стороны, противолежащей этому углу, к сумме квадратов двух других сторон треугольника.
Алгоритм нахождения медианы треугольника по теореме косинусов следующий:
- Определить длины сторон треугольника.
- Вычислить косинусы углов треугольника по формуле: cos(A) = (b^2 + c^2 - a^2) / (2 * b * c), cos(B) = (a^2 + c^2 - b^2) / (2 * a * c), cos(C) = (a^2 + b^2 - c^2) / (2 * a * b), где a, b, c – длины сторон треугольника, A, B, C – соответственно углы треугольника противолежащие сторонам a, b, c.
- Найдите медиану, соединяющую вершину A с серединой противоположной стороны a, по формуле: m = (1/2) * sqrt(2 * b^2 + 2 * c^2 - a^2).
Таким образом, зная длины сторон треугольника, можно легко вычислить медиану треугольника по теореме косинусов, применяя описанный алгоритм. Этот метод позволяет получить точные результаты и использовать их для различных геометрических задач.
Медиана треугольника по теореме косинусов
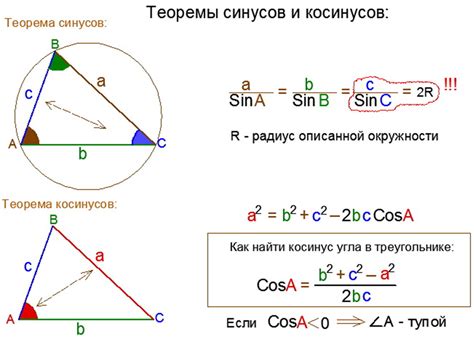
В общем виде, теорема косинусов гласит: c^2 = a^2 + b^2 - 2ab * cos(C), где c – длина стороны, противоположной углу C, a и b – длины других двух сторон, а cos(C) – косинус угла C.
Для вычисления медианы, исходящей из вершины A, можно использовать следующую формулу:
- Вычисляем длины сторон треугольника: a, b, и c.
- Вычисляем значение косинуса угла C при помощи теоремы косинусов.
- Вычисляем длину медианы, исходящей из вершины A, используя формулу: ma = sqrt(2b^2 + 2c^2 - a^2) / 2, где ma – длина медианы, a – длина стороны противоположной вершине A, b и c – длины других двух сторон треугольника.
Аналогично можно рассчитать длины медиан, исходящих из вершин B и C. После вычисления длин всех трех медиан можно приступить к определению их точек пересечения – центра масс треугольника.
Таким образом, расчет медианы треугольника по теореме косинусов представляет собой достаточно простую процедуру, которая позволяет найти длины всех трех медиан и точку их пересечения – центр масс треугольника.
Определение и суть теоремы косинусов для треугольника
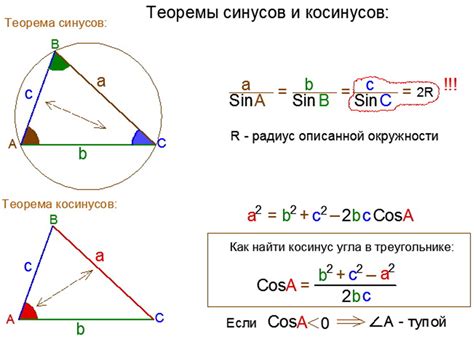
Пусть у нас есть треугольник ABC, где стороны обозначены как a, b и c, а противолежащие им углы обозначены как A, B и C соответственно. Тогда теорема косинусов утверждает, что квадрат длины одной из сторон равен сумме квадратов длин двух других сторон минус двойное произведение этих сторон на косинус между ними:
| a2 = b2 + c2 - 2bc * cos(A) |
| b2 = a2 + c2 - 2ac * cos(B) |
| c2 = a2 + b2 - 2ab * cos(C) |
Теорема косинусов может быть полезна для решения широкого спектра геометрических задач, включая вычисление длин сторон, углов и площадей треугольников. Основные применения теоремы косинусов включают нахождение медианы и высоты треугольника.
Расчет медианы треугольника по теореме косинусов
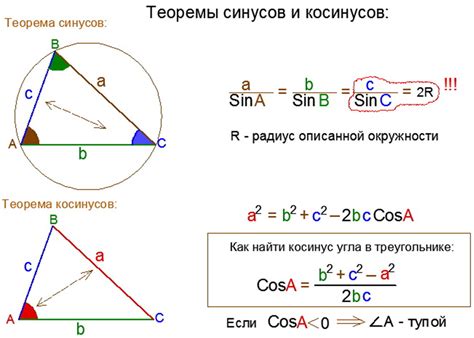
Для вычисления медианы треугольника по теореме косинусов следуйте данным шагам:
- Определите длины сторон треугольника, обозначим их a, b, c.
- Найдите угол между медианой и соответствующей стороной треугольника, обозначим его как угол α.
- Используя теорему косинусов, вычислите длину медианы по следующей формуле:
Медиана треугольника:
медиана = sqrt(2 * b^2 + 2 * c^2 - a^2) / 2
После получения значения медианы можно использовать его для различных расчетов и анализа треугольника.