Как найти медиану треугольника при помощи циркуля?

Медиана треугольника - это отрезок, соединяющий один из вершин треугольника с точкой пересечения двух других медиан. Этот отрезок делит медиану на две равные части и является одной из наиболее важных геометрических характеристик треугольника.

Однако, часто возникает задача найти медиану треугольника при отсутствии линейки, но при наличии циркуля. В таком случае можно использовать метод построения медианы треугольника циркулем.

Для построения медианы нужно провести две медианы, пересечение которых будет являться точкой, через которую пройдет искомая медиана. Важно отметить, что точка пересечения медиан треугольника называется центром тяжести и является серединой этой медианы.

Построение медианы треугольника циркулем - это несложная и эффективная геометрическая процедура. Она позволяет определить медиану треугольника и найти его центр тяжести без использования других инструментов, кроме циркуля. При использовании этого метода важно следовать инструкциям и бережно обращаться с циркулем, чтобы получить точный и правильный результат.

Зачем нужно находить медиану треугольника циркулем

• Определение центра тяжести: Медиана треугольника проходит через его центр тяжести, точку, в которой сумма всех масс треугольника сосредоточена. Нахождение центра тяжести может быть полезно, например, при проектировании равномерно нагруженных конструкций.
• Нахождение высоты: Медиана, проходящая через вершину треугольника и середину противолежащей стороны, является высотой треугольника. Нахождение высоты треугольника может быть важным для решения задач геометрии и строительства.
• Определение перпендикулярных линий: Медиана треугольника, проходящая через вершину и середину стороны, перпендикулярна этой стороне. Это свойство медианы можно использовать для нахождения перпендикулярных линий в геометрических конструкциях.
• Решение задач с использованием гармонических соотношений: Медиана треугольника является половиной медианы, выходящей из другой вершины. Это отношение медиан может быть использовано при решении задач, связанных с гармоническими соотношениями в геометрии.

Обнаружение и использование этих свойств медиан треугольника может значительно облегчить некоторые геометрические расчеты и строительные проекты. Поэтому нахождение медианы треугольника циркулем является полезным навыком для инженеров, архитекторов и математиков.

Описание медианы треугольника

Медиана является отрезком, который делит другую сторону треугольника пополам. Она проходит через середину стороны и точку, которая является вершиной треугольника.

Медиана треугольника является важным элементом геометрии, так как она имеет несколько интересных свойств и применений. Например, центроид треугольника разделяет каждую медиану в отношении 2:1. То есть, расстояние от вершины треугольника до центроида всегда в два раза больше расстояния от центроида до середины соответствующей медианы.

Медианы также играют важную роль в построении геометрических фигур и решении задач, связанных с треугольниками. Так, например, медианы треугольника пересекаются в одной точке, которую можно использовать для построения центроида или для нахождения центральной симметрии треугольника. Медианы также могут быть использованы для вычисления площади треугольника или его сторон, основываясь на определенных формулах и свойствах треугольника.

Таким образом, медиана треугольника является важным элементом геометрии, который имеет множество свойств и применений. Понимание медианы и ее свойств помогает в решении задач и изучении треугольников в геометрии.

Медиана как средняя линия треугольника

Медианы являются основными элементами треугольника и имеют несколько интересных свойств:

• Все три медианы пересекаются в одной точке, называемой центром масс треугольника.
• Медиана, соединяющая вершину треугольника с серединой противоположной стороны, делит площадь треугольника на две равные части.
• Длина каждой медианы равна сумме половин длин оставшихся сторон треугольника.

Медианы играют важную роль в геометрии и имеют множество применений. Например, они используются для нахождения центра барицентрической координаты треугольника, в задачах анализа диаграммы Вороного и во многих других областях.

Вычисление медианы треугольника циркулем возможно, однако требует определенных навыков и соблюдения определенных условий. Для этого можно использовать простые геометрические построения, такие как построение середины стороны треугольника и соединение ее с вершиной.

В итоге, медиана - это важный элемент треугольника, который помогает нам понять его структуру и особенности. Она является средней линией, делит треугольник на две равные части и проходит через его центр масс.

Как найти две медианы треугольника

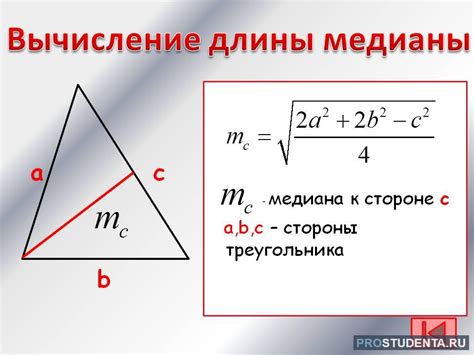
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Для любого треугольника можно найти две медианы, которые пересекаются в точке, называемой центром масс треугольника.

Для нахождения медианы треугольника, необходимо:

Шаг 1: Выберите две вершины треугольника и поставьте циркуль в одну из этих вершин. Разметьте на отрезке между этой вершиной и противоположной стороной точку, соответствующую половине длины этого отрезка.

Шаг 2: Установите циркуль во вторую вершину треугольника и сделайте заметку на противоположной стороне в месте, где циркуль пересекается с этой стороной. Обозначьте эту точку как середину стороны.

Шаг 3: Соедините полученные точки заметок циркулем. Полученный отрезок будет первой медианой треугольника.

Примечание: Чтобы найти вторую медиану треугольника, повторите те же шаги, начиная с других вершин треугольника.

Таким образом, используя циркуль, можно легко найти две медианы треугольника и определить их точку пересечения - центр масс треугольника. Этот метод является одним из способов геометрического анализа треугольников и имеет множество приложений в различных областях науки и инженерии.

Какая из медиан является медианой треугольника

Из всех медиан треугольника, самая длинная является медианой треугольника. Эта медиана проходит через вершину треугольника и середину противоположной стороны, деля её на две равные части. Медианы, соединяющие другие вершины с серединами противоположных сторон, не являются медианами треугольника в строгом смысле, хотя и являются важными отрезками в геометрии треугольников.

Определение медианы треугольника имеет большое значение в геометрии и в различных приложениях на практике. Знание о том, какая медиана является медианой треугольника, позволяет решать разнообразные задачи, связанные с треугольниками, в том числе вычислять площадь треугольника, определять его центр тяжести и многое другое.

Таким образом, из всех медиан треугольника самая длинная медиана является медианой треугольника. Этот факт играет важную роль в геометрии и позволяет решать различные задачи, связанные с треугольниками.

Метод нахождения медианы треугольника циркулем

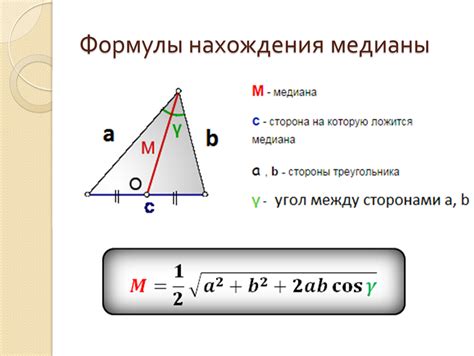
Для начала проведем стороны треугольника. Пусть A, B и C - вершины треугольника, а a, b и c - соответствующие стороны.

Далее, найдем середину стороны a - точку M. Для этого, с помощью циркуля, проведем окружность с радиусом a и центром в точке A. От точки пересечения окружности с прямой BC отложим отрезок, равный половине стороны a. Полученная точка M будет серединой стороны a.

Аналогично, найдем середины сторон b и c - точки N и P соответственно.

Далее, проведем медиану из вершины A. С помощью циркуля, с центром в точке M, проведем окружность, проходящую через точку B. Пусть эта окружность будет радиуса r. Она пересекает сторону c в точке K. Медиана AM пересекает сторону BC в точке L. От точки L проведем прямую, параллельную стороне AB, которая пересекает сторону AC в точке D.

Точка D - середина стороны BC, а отрезок AD - медиана треугольника ABC из вершины A.

Аналогичным образом проводятся медианы из вершин B и C, что позволяет найти все медианы треугольника циркулем.

Таким образом, метод нахождения медианы треугольника с использованием циркуля состоит из последовательного проведения окружностей, находящихся на серединах сторон треугольника, и поиска пересечений этих окружностей с прямыми, образованными медианами.

Пример нахождения медианы треугольника циркулем

1. Нарисуйте треугольник на листе бумаги.
2. Установите циркуль на одной из вершин треугольника и откройте его на расстояние, превышающее половину длины противоположной стороны.
3. Сделайте окружность, касающуюся этой стороны треугольника в точке середины стороны.
4. Повторите шаги 2 и 3 для двух других вершин треугольника.
5. Все три окружности должны пересечься в одной точке, и это будет точка пересечения медиан треугольника.

Таким образом, вы можете использовать циркуль для нахождения медиан треугольника. Этот метод пригодится в задачах геометрии и конструктивной геометрии.

Применение медианы треугольника в геометрии

• Центр масс: Медианы треугольника пересекаются в одной точке, называемой центром масс. Эта точка является средним значением позиций вершин треугольника и имеет равное расстояние до каждой из вершин. Центр масс является важным понятием в физике и технике, а также используется в задачах оптимизации.
• Контроль нарушений: В некоторых задачах геометрии, медиана может использоваться для контроля нарушений. Например, если разбить одну из медиан на две равные части, то ее точка пересечения с противоположной стороной будет представлять серединную точку этой стороны. Если точка пересечения отклоняется от серединной точки, это может указывать на нарушение геометрической формы.
• Разделение площадей: Медианы также могут использоваться для разделения площадей внутри треугольника. Если провести медиану из одной вершины до противоположной стороны, она разделит треугольник на две равные площади. Это может быть полезно, например, при решении задачи о нахождении центра тяжести треугольника.

Таким образом, медиана треугольника имеет множество применений в геометрии. Она используется для определения центра масс, контроля нарушений и разделения площадей внутри треугольника. Знание этих применений позволяет геометрам применять медианы для решения различных задач и анализа треугольников.