Как найти медиану треугольника в 7 классе геометрии — идеальное объяснение и шаги решения

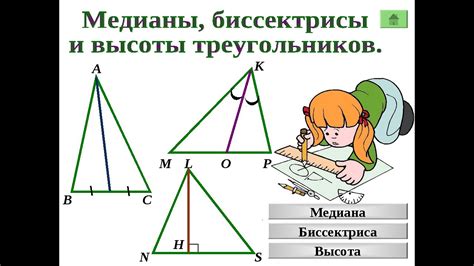
Медиана треугольника - это линия, соединяющая вершину треугольника с серединой противоположной стороны. Найти медиану треугольника может показаться сложным заданием, однако с помощью простых геометрических действий, вы сможете справиться с этой задачей даже на уроке геометрии в 7 классе!

Прежде чем начать поиск медианы, необходимо разобраться в определении треугольника и его основных элементах. У треугольника три стороны и три угла, а также центр масс, который находится на пересечении медиан. Поэтому медианы являются осью симметрии треугольника.

Теперь перейдем к поиску медианы. Для этого нужно выбрать любую вершину треугольника и провести линию от этой вершины до середины противоположной стороны. Получившеяся линия и будет искомой медианой.

Понятие медианы треугольника

Медианы обозначаются буквами m_a, m_b и m_c. Например, m_a соединяет вершину A с серединой противолежащей стороны BC.

Медианы являются особыми линиями треугольника, которые проходят через его центр тяжести и делят треугольник на шесть равных треугольников. Они также пересекаются в одной точке, называемой центром тяжести треугольника.

Медианы треугольника имеют ряд интересных свойств. Например, медиана треугольника равна половине суммы длин остальных двух медиан. Также, у треугольника и его медиан обязательно существует взаимосвязь: если соединить концы медиан треугольника, то образуется новый треугольник, который подобен исходному.

Использование медиан треугольника помогает в решении геометрических задач, например, в определении центра тяжести треугольника, нахождении площади треугольника и других вопросах, связанных с его конструкцией и свойствами.

Определение и свойства медианы треугольника

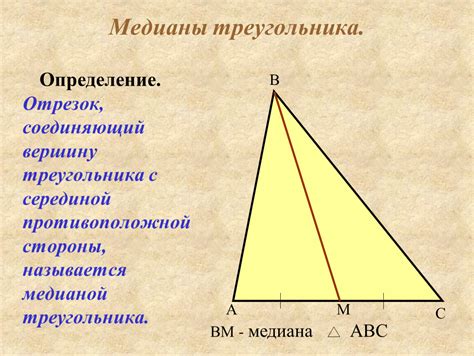
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. Точка пересечения медиан называется центром масс треугольника или его барицентром.

У медиан треугольника есть несколько свойств:

1. Медианы треугольника делятся центром масс треугольника на три равные части. То есть, длина каждой медианы равна сумме длин двух других медиан.

2. Медианы треугольника пересекаются в одной точке, которая является центром масс треугольника. Исключением может быть треугольник с равными сторонами, в котором медианы совпадают и пересекаются в одной точке.

3. Медиана треугольника делит его площадь на 6 равных треугольников.

Знание определения и свойств медианы треугольника помогает решать задачи на нахождение медианы и использовать ее свойства для получения дополнительной информации о треугольнике.

Решение задачи по нахождению медианы треугольника

Для решения задачи по нахождению медианы треугольника нужно выполнить следующие шаги:

1. Найдите середины всех сторон треугольника.
2. Проведите прямые линии, соединяющие вершины треугольника с соответствующими серединами сторон. Эти прямые называются медианами треугольника и пересекаются в одной точке - центре тяжести треугольника.
3. Найдите точку пересечения медиан и обозначьте ее как точку G.
4. Проведите прямую линию, соединяющую точку G с вершиной треугольника, противоположной стороне, на которой находится точка G. Эта прямая называется медианой треугольника и делит ее на две части, равные по длине.

Таким образом, найденная прямая линия, соединяющая середину стороны треугольника с противоположной вершиной, является медианой треугольника. Она делит треугольник на две равные по площади части.

Нахождение медианы треугольника важно для определения центра тяжести и равнодоложности массы треугольника. Это позволяет упростить анализ и решение различных задач, связанных с геометрией треугольников.

Шаги для нахождения медианы треугольника

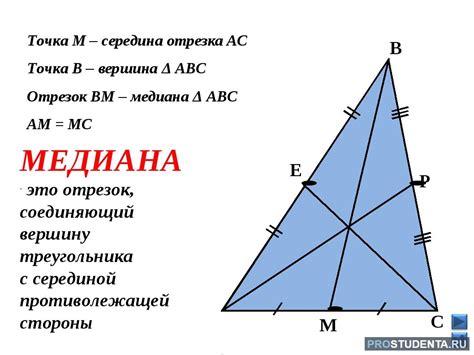
1. Нарисуйте треугольник с помощью линейки и карандаша на листе бумаги.
2. Определите середины каждой из трех сторон. Для этого можно использовать линейку, чтобы найти середину каждой стороны.
3. Соедините каждую вершину треугольника с соответствующей серединой противолежащей стороны. Полученные линии будут медианами треугольника.
4. Укажите на рисунке точку пересечения трех медиан. Эта точка называется центром тяжести треугольника.

Теперь вы можете уверенно говорить о том, как найти медиану треугольника и визуально представить себе процесс. Не забывайте, что медианы треугольника делятся в точке пересечения в отношении 2:1, то есть каждая медиана делит другую на две равные части.