Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой. В таком треугольнике можно вычислить различные параметры, включая медиану, которая является одной из важных характеристик этой фигуры.
Медиана - это линия, которая соединяет любую вершину треугольника с серединой противоположной стороны. В равнобедренном треугольнике все медианы пересекаются в одной точке, которая делит каждую медиану в отношении 2:1.
Чтобы найти медиану в равнобедренном треугольнике, нужно знать его размеры. Обозначим одну из равных сторон треугольника как a и достаточно найти длину медианы, выпущенной из угла при этой стороне. Но прежде чем мы погрузимся в расчеты, давайте рассмотрим подробный алгоритм для нахождения медианы в равнобедренном треугольнике.
Как найти медиану в равнобедренном треугольнике
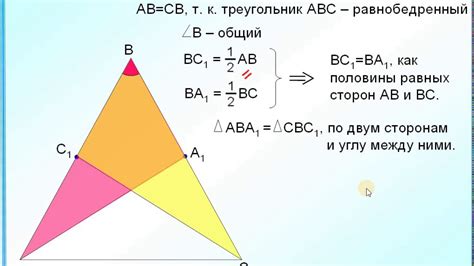
Для нахождения медианы в равнобедренном треугольнике можно использовать несколько методов. Один из простых способов - использование свойств равнобедренного треугольника и применение формулы для нахождения медианы.
Шаги для нахождения медианы в равнобедренном треугольнике:
- Определите длину основания треугольника. Для этого измерьте расстояние между вершинами основания.
- Делите длину основания пополам, чтобы найти точку, в которой медиана пересекает основание. Эта точка будет серединой основания.
- Из вершины треугольника проведите линию, соединяющую её с серединой основания. Эта линия будет медианой.
Применив эти шаги, вы сможете определить медиану в равнобедренном треугольнике и использовать эту информацию для решения различных задач и заданий, связанных с равнобедренными треугольниками.
Примечание: Медиана в равнобедренном треугольнике также является биссектрисой угла при вершине, а также высотой, опущенной из вершины на основание.
Подробное руководство

Для нахождения медианы в равнобедренном треугольнике нужно выполнить несколько шагов.
1. Определите длину основания треугольника. Поскольку треугольник равнобедренный, то его основание будет являться самой длинной из сторон.
2. Используя теорему Пифагора, найдите длину боковой стороны треугольника. Для этого возведите в квадрат половину длины основания и вычтите из него квадрат высоты треугольника: a^2 - h^2 = c^2.
3. Найдите длину отрезка, соединяющего середину основания и вершину треугольника. Для этого разделите длину боковой стороны на 2: c/2 = m.
4. Медиана треугольника будет линией, которая соединяет вершину треугольника с серединой основания.
Итак, следуя этому подробному руководству, вы сможете легко найти медиану в равнобедренном треугольнике. Удачи!
Треугольник и его основные характеристики
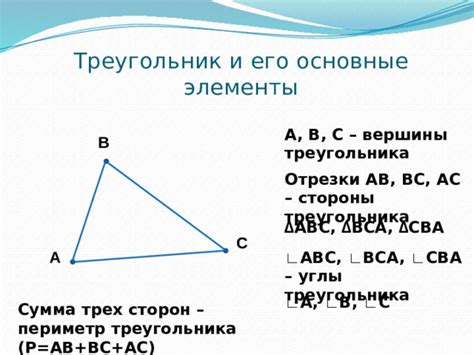
В равнобедренном треугольнике две стороны равны друг другу. Такой треугольник имеет три основные характеристики: стороны, углы и медианы.
- Стороны: В равнобедренном треугольнике две стороны имеют одинаковую длину, а третья сторона отличается от них.
- Углы: У равнобедренного треугольника два угла между равными сторонами также равны и называются основными углами. Третий угол, между неравными сторонами, называется вершинным углом.
- Медианы: Медианы треугольника - это отрезки, соединяющие вершину треугольника с серединами противоположных сторон. В равнобедренном треугольнике медианы также являются биссектрисами (полусуммами) вершинных углов.
Изучение основных характеристик треугольника, таких как стороны, углы и медианы, позволяет лучше понять его свойства и использовать их для решения геометрических задач.
Определение медианы и ее свойства
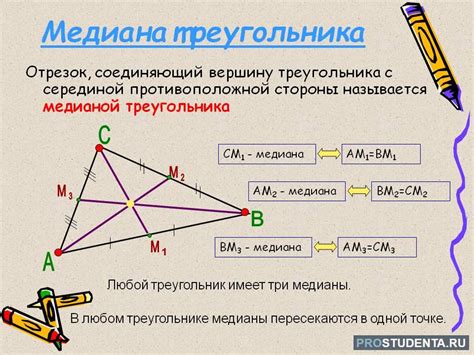
Свойства медианы в равнобедренном треугольнике:
- Медиана делит противоположную сторону на две равные части. То есть, отрезок медианы от вершины до середины стороны делится на две равные отрезка.
- Медиана является высотой и биссектрисой равнобедренного треугольника. Это означает, что медиана перпендикулярна к противоположной стороне и делит ее пополам, а также делит вершинный угол пополам.
- Медиана пересекается с осями симметрии равнобедренного треугольника. Это означает, что точка пересечения медиан является центром симметрии треугольника.
Использование свойств медианы в равнобедренном треугольнике позволяет нам находить различные величины, такие как площадь треугольника, высоту, углы и другие характеристики, которые могут быть полезными при решении геометрических задач.
Формула вычисления длины медианы
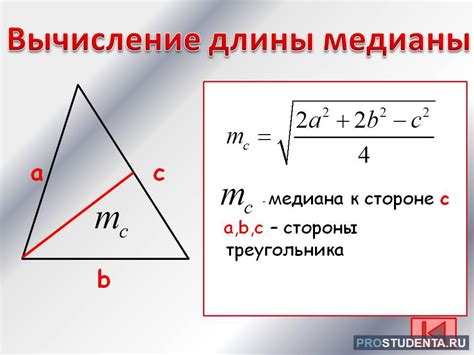
медиана = √(2b² + 2c² - a²) / 2
Где:
b и c - длины равных сторон треугольника (катеты)
a - длина основания треугольника (гипотенуза)
Для применения формулы, известные значения сторон треугольника должны быть подставлены в соответствующие переменные. После этого, простыми математическими вычислениями можно определить длину медианы.
Практический пример расчета медианы

Для наглядности и лучшего понимания процесса расчета медианы в равнобедренном треугольнике предлагаем рассмотреть следующий практический пример:
Дан равнобедренный треугольник ABC с основанием AC и высотой h, где AB=BC. Найдем медиану треугольника.
| Величина | Обозначение | Значение |
|---|---|---|
| Длина основания AC | a | 10 см |
| Высота треугольника h | h | 8 см |
1. Вычисляем длину медианы AM с помощью формулы медианы в равнобедренном треугольнике:
AM = 2/3 * h
Подставляем известные значения:
AM = 2/3 * 8 см
AM = 16/3 см
2. Получаем ответ:
Медиана треугольника AM равна 16/3 см.
Таким образом, медиана треугольника в данном примере равна 16/3 см.