Медиана является одной из наиболее важных характеристик треугольника. В равнобедренном треугольнике медиана является также высотой и биссектрисой. Она делит основание треугольника пополам и перпендикулярна ему. Поэтому знание формулы для нахождения медианы в равнобедренном треугольнике является неотъемлемым элементом в геометрии.
Формула нахождения медианы в равнобедренном треугольнике имеет простой вид. Она равна половине квадрата корня из суммы квадратов половины основания и высоты треугольника. Математически это выглядит следующим образом:
медиана = 0,5 × √(0,5 × основание2 + высота2)
Рассмотрим пример: у нас есть равнобедренный треугольник, у которого основание равно 10 и высота равна 8. Чтобы найти медиану данного треугольника, мы можем использовать формулу. Подставив значения, получим:
медиана = 0,5 × √(0,5 × 102 + 82) = 0,5 × √(0,5 × 100 + 64) = 0,5 × √(50 + 64) = 0,5 × √114 = 0,5 × 10,68 = 5,34
Таким образом, медиана равнобедренного треугольника с основанием 10 и высотой 8 равна 5,34. Эта величина может быть полезна при решении различных геометрических задач и упрощении вычислений.
Примеры и формула вычисления медианы в равнобедренном треугольнике
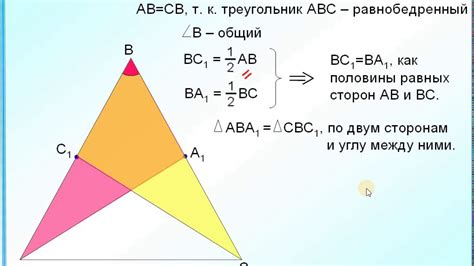
Для вычисления медианы в равнобедренном треугольнике с известными длинами сторон используется следующая формула:
медиана (m) = √((2b^2 + a^2) / 4)
где a - длина равных сторон, b - длина основания треугольника.
Пример 1:
Дан равнобедренный треугольник со стороной a = 5 и основанием b = 6.
Используя формулу, найдем длину медианы:
m = √((2 * 6^2 + 5^2) / 4) = √((72 + 25) / 4) = √(97 / 4) ≈ √24.25 ≈ 4.92.
Таким образом, длина медианы равнобедренного треугольника составляет примерно 4.92.
Пример 2:
Дан равнобедренный треугольник со стороной a = 7 и основанием b = 8.
Используя формулу, найдем длину медианы:
m = √((2 * 8^2 + 7^2) / 4) = √((128 + 49) / 4) = √(177 / 4) ≈ √44.25 ≈ 6.65.
Таким образом, длина медианы равнобедренного треугольника составляет примерно 6.65.
Таким образом, с использованием формулы можно легко вычислить длину медианы в равнобедренном треугольнике, если известны длины его сторон.
Примеры определения медианы в равнобедренном треугольнике
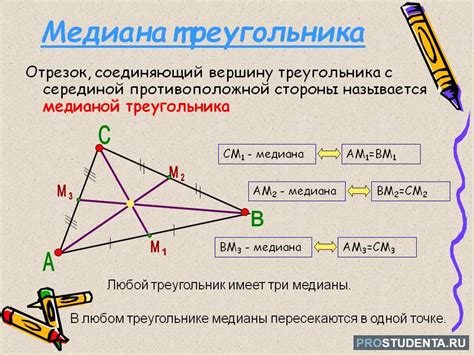
Рассмотрим пример. У нас есть равнобедренный треугольник ABC, где AB = AC. Чтобы найти медиану, нам нужно найти середину стороны BC. Для этого мы берем штангенциркуль и измеряем длины стороны BC и делим ее пополам. Найденная точка будет являться серединой стороны BC и началом медианы.
Еще один пример. Допустим, у нас есть треугольник XYZ, где YZ = YX. Нам нужно найти медиану треугольника, которая проходит через вершину Y и середину стороны XZ. Мы можем использовать линейку или другой измерительный инструмент для определения середины стороны XZ. Найденная точка будет началом медианы.
Таким образом, нахождение медианы в равнобедренном треугольнике не представляет сложности, если известна сторона, которую нужно разделить на две равные части. Это особенно полезно при решении геометрических задач или при построении треугольников.
Формула для вычисления медианы в равнобедренном треугольнике
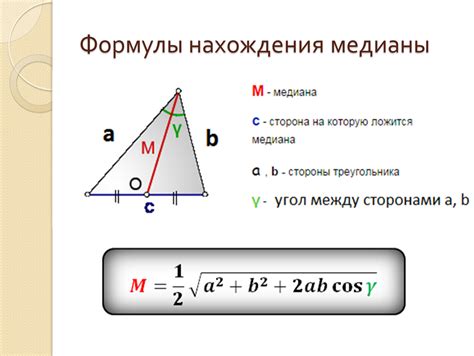
Для вычисления медианы в равнобедренном треугольнике можно использовать следующую формулу:
m = sqrt((2b^2 + c^2 - a^2) / 4)
Где:
- m - медиана
- a - длина основания треугольника
- b - длина боковой стороны треугольника
- c - длина медианы
Например, если длина основания равна 8 единиц, а длина боковой стороны равна 6 единиц, то для вычисления длины медианы воспользуемся формулой:
m = sqrt((2 * 6^2 + 8^2 - 6^2) / 4)
Вычисляем значения:
- m = sqrt((2 * 36 + 64 - 36) / 4)
- m = sqrt((72 + 64 - 36) / 4)
- m = sqrt(100 / 4)
- m = sqrt(25)
- m = 5
Таким образом, длина медианы в данном равнобедренном треугольнике составляет 5 единиц.