Окружность - одна из фундаментальных геометрических фигур, и понимание ее свойств очень важно для решения различных задач. Одним из важных параметров, определяющих окружность, является мера дуги. Мера дуги - это длина области окружности, ограниченной двумя ее точками.
Найти меру дуги окружности можно с помощью специальной формулы. Если известен радиус окружности и угол, закрываемый дугой, формула будет следующей: длина дуги равна произведению радиуса на значение угла в радианах.
При использовании этой формулы важно помнить, что угол должен быть задан в радианах, поскольку это единица измерения, которая связана с радиусом и длиной дуги окружности. Если угол задан в градусах, его следует перевести в радианы, умножив на коэффициент π/180.
Зная формулу для нахождения меры дуги окружности, вы сможете решать разнообразные задачи, связанные с геометрией и тригонометрией, а также визуализировать и анализировать различные физические и математические процессы.
Что такое мера дуги окружности?
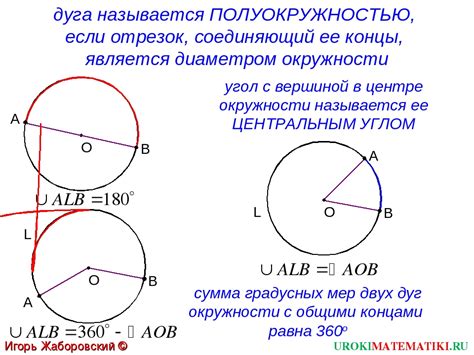
Для вычисления меры дуги окружности существует формула, которая основана на отношении длины дуги к длине полной окружности. Мера дуги может быть выражена как произведение угла, измеренного в радианах или градусах, на радиус окружности. Формула для вычисления меры дуги может быть записана следующим образом:
| Мера дуги | = | Угол | * | Радиус |
Например, если угол между двумя точками на окружности равен 45 градусов, а радиус окружности равен 5 сантиметров, то мера дуги будет равна 45 градусов * 5 сантиметров = 225 сантиметров.
Мера дуги окружности является важным понятием в геометрии и находит свое применение в различных областях, таких как астрономия, инженерия и природные науки.
Почему важно найти меру дуги окружности?
Одним из основных применений меры дуги окружности является геодезия. В сфере картографии и навигации, знание меры дуги окружности позволяет точно определить расстояние между двумя точками на поверхности Земли. Это особенно важно в мореплавании, авиации и космической навигации, где точность определения координат и расстояний играет решающую роль в безопасности и эффективности передвижения.
Мера дуги окружности также находит применение в производственных процессах, связанных с обработкой материалов. Зная меру дуги окружности, можно рассчитать необходимое количество материала для изготовления круглых деталей, таких как трубы, кабели, колеса и многое другое. Это позволяет оптимизировать производственные процессы, снижая затраты на материалы и повышая эффективность технологических операций.
| Область применения | Пример |
|---|---|
| Навигация и картография | Определение расстояния между двумя точками на поверхности Земли |
| Производство | Рассчет необходимого количества материала для изготовления круглых деталей |
| Архитектура и строительство | Определение длины окружности для правильной укладки кабелей и трубопроводов |
| Медицина | Рассчет длины различных каналов и трубок в организме человека |
| Физика | Определение пути и скорости движения тела по окружности |
Таким образом, нахождение меры дуги окружности является необходимым для решения разнообразных задач в геометрии, науке и технике. Обладая знаниями о методах определения меры дуги окружности, мы можем применять их в реальных ситуациях, что позволяет улучшать точность измерений, повышать эффективность процессов и достигать лучших результатов в своей деятельности.
Зачем нужна мера дуги окружности
Во-первых, мера дуги окружности позволяет нам выразить угол в градусах или радианах. Таким образом, используя меру дуги, мы можем удобно описывать и сравнивать различные углы и измерять повороты в пространстве.
Кроме того, мера дуги окружности является важным понятием в геометрии. Она позволяет рассчитывать длину окружности, его площадь и другие характеристики. Например, если нам необходимо вычислить, сколько плиток потребуется для заливки круглого бассейна, мы можем воспользоваться мерой дуги окружности, чтобы рассчитать общую длину его края.
Кроме того, мера дуги окружности может быть использована в различных научных и технических областях. Например, она может быть важной для разработки таких устройств, как перископы или угломеры, где необходимо знать угол поворота относительно начального положения.
Таким образом, мера дуги окружности имеет широкий спектр применений в различных областях, помогая измерять и описывать углы, рассчитывать длину окружности и площадь, а также использоваться в научных и технических расчетах.
Как найти меру дуги окружности без формул?
Хотите найти меру дуги окружности, но не хотите использовать формулы? Вполне возможно! Существует несколько способов определить меру дуги без применения математических формул.
Первый способ - использовать измерительные инструменты. Возьмите линейку или мерную ленту и измерьте длину дуги непосредственно на реальной окружности. Результатом будет прямое значение меры дуги в выбранных единицах измерения.
Второй способ - использовать угломерный инструмент. Поместите окружность внутри угломера и измерьте угол, который образуется между точками начала и конца дуги. Затем, используя знание о том, что окружность полный угол равен 360 градусов (или 2π радиан), определите, какая доля полного угла приходится на вашу дугу. Мера дуги будет пропорциональна этому значению.
Третий способ - использовать долю длины окружности. Если вы ищете меру дуги, которая составляет 1/4 от полной окружности, достаточно найти 1/4 от длины окружности и использовать этот результат в качестве меры дуги.
Используя эти методы, вы можете найти меру дуги окружности без использования математических формул. Однако, имейте в виду, что они могут быть менее точными, чем использование формул, особенно при работе с большими окружностями.
Геометрический метод определения меры дуги

Для определения меры дуги окружности можно использовать геометрический метод, основанный на измерении длины дуги с помощью инструментов.
Шаги геометрического метода определения меры дуги:
- Нарисуйте окружность с помощью циркуля и линейки или используйте готовый графический образец.
- Выберите точку начала дуги и пометьте ее на окружности.
- Выберите точку окончания дуги и пометьте ее на окружности.
- Измерьте длину отрезка между начальной и конечной точками дуги с помощью линейки или наложив его на измерительную шкалу на экране, если используется программное обеспечение для рисования.
Полученное значение длины отрезка будет являться приближенной мерой дуги окружности. Чтобы получить точное значение, необходимо использовать математическую формулу:
Длина дуги = (Мера угла / 360) * (2 * π * радиус)
Где мера угла измеряется в градусах, π - математическая константа, равная приблизительно 3.14159, и радиус - расстояние от центра окружности до ее границы.
Используя данный метод и формулу, вы сможете точно определить меру дуги окружности и применить ее в решении геометрических задач.
Измерение меры дуги с помощью профессиональных инструментов

Когда точность измерений критически важна, используются специальные профессиональные инструменты для определения меры дуги окружности. Они обеспечивают более точные и надежные результаты, чем ручные измерения.
Один из таких инструментов - измеритель дуги. Это прибор, который имеет специальную шкалу, рассчитанную на измерение меры дуги окружности. Для измерения необходимо правильно установить измеритель на начальной точке дуги, затем следовать по дуге и считывать со шкалы конечное значение.
Другой инструмент - лазерный измеритель. Он использует лазерный луч для отображения меры дуги на поверхности. Лазерный измеритель устанавливается на начальной и конечной точках дуги и автоматически рассчитывает ее меру.
Компьютеризированные измерительные системы также широко используются для измерения меры дуги. Они позволяют точно и быстро измерить любую дугу окружности с помощью специальных программ и датчиков.
Профессиональные инструменты для измерения меры дуги окружности обеспечивают высокую точность и повторяемость измерений. Они широко применяются в научных и инженерных исследованиях, производственных процессах и других областях, где требуется высокая точность измерений дуги окружности.
Как найти меру дуги окружности с помощью формулы?
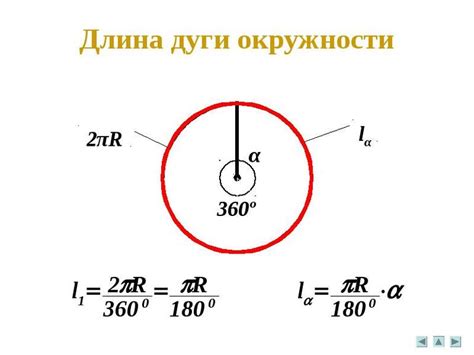
Формула для расчета меры дуги окружности имеет вид:
Мера дуги = (центральный угол / 360) * 2 * π * радиус
Для использования этой формулы необходимо знать значения центрального угла и радиуса окружности. Центральный угол измеряется в градусах, а радиус - в единицах длины (например, сантиметрах или метрах).
Пример:
Допустим, у нас есть окружность с радиусом 5 см и центральным углом 90°. Чтобы найти меру дуги этой окружности, мы можем использовать формулу:
Мера дуги = (90 / 360) * 2 * π * 5 = 1/4 * 2 * π * 5 = 1/2 * π * 5 ≈ 7,854 см
Таким образом, мера дуги этой окружности составляет около 7,854 см.
Использование формулы позволяет легко и точно находить меру дуги окружности, основываясь на ее радиусе и центральном угле.
Объяснение формулы для расчета меры дуги
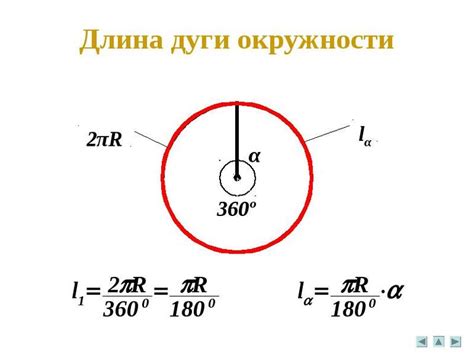
Для расчета меры дуги можно использовать формулу:
Длина дуги = (Угол / 360°) * (2π * r)
В этой формуле:
- Длина дуги – обозначает длину секции окружности, выраженную в единицах длины;
- Угол – представляет собой меру угла дуги в градусах;
- 360° – количество градусов в полном обороте окружности;
- 2π – это число π, которое примерно равно 3,14159 и представляет собой отношение длины окружности к ее диаметру;
- r – радиус или расстояние от центра окружности до точки на окружности.
Таким образом, формула позволяет нам вычислить длину дуги окружности, основываясь на ее радиусе и угле дуги. Зная длину дуги, можно рассчитать различные параметры и свойства окружности, такие как площадь сектора или периметр сектора.
Примеры использования формулы для нахождения меры дуги
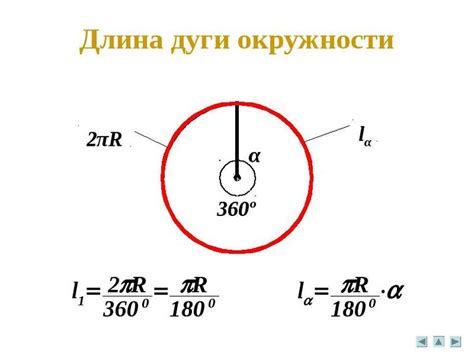
Пример 1:
Пусть у нас имеется окружность радиусом 5 сантиметров. Нам известно, что центральный угол, под которым находится дуга, равен 60 градусам. Как найти меру дуги, соответствующей данному углу?
Решение:
Для решения задачи мы можем использовать формулу, которая гласит, что мера дуги равна произведению центрального угла в радианах на радиус окружности.
Мера дуги = (центральный угол в радианах) * (радиус окружности)
Сначала нам необходимо перевести угол из градусов в радианы:
Угол в радианах = (угол в градусах * π) / 180°
Угол в радианах = (60 * 3.14) / 180° ≈ 1.047 радиана
Теперь мы можем найти меру дуги:
Мера дуги = 1.047 * 5 см ≈ 5.236 см
Пример 2:
Представим ситуацию, когда у нас имеется окружность, радиус которой равен 10 метров. Теперь нам известна мера дуги, равная 15 метрам. Как найти центральный угол, под которым находится эта дуга?
Решение:
Мы можем использовать ту же самую формулу для нахождения центрального угла:
Центральный угол = (мера дуги) / (радиус окружности)
Центральный угол = 15 м / 10 м ≈ 1.5 радиана
Таким образом, центральный угол под которым находится данная дуга окружности составляет примерно 1.5 радиана.
Эти примеры демонстрируют использование формулы для нахождения меры дуги окружности. Зная либо меру дуги, либо центральный угол, под которым находится дуга, мы можем использовать эту формулу, чтобы найти другую известную величину.