Модуль равнодействующих сил – это величина, характеризующая суммарное воздействие нескольких сил на объект. Ее нахождение осуществляется путем сложения векторов, которые представляют эти силы. Определение модуля равнодействующих сил является важным этапом в решении задач механики и физики.

Существует несколько методов вычисления модуля равнодействующих сил. Один из наиболее распространенных методов – метод правильного многоугольника. Он основан на разложении каждой силы на горизонтальную и вертикальную составляющие. Затем по этим составляющим строится полигон, в котором диагональ является равнодействующей силы. Модуль равнодействующей силы можно найти с помощью теоремы Пифагора.

Другой метод – метод прямоугольников. В этом методе силы разлагаются на составляющие, параллельные осям координат. Затем составляющие складываются по отдельности по горизонтале и вертикале. Модуль равнодействующей силы находится с использованием теоремы косинусов или теоремы Пифагора.

Примеры применения этих методов помогут лучше понять, как найти модуль равнодействующих сил по векторам. Рассмотрим, например, случай, когда на объект действуют две силы: F1 с модулем 10 Н и F2 с модулем 5 Н. Силы действуют под углами 30 градусов и 60 градусов соответственно. Применяя метод правильного многоугольника или метод прямоугольников, можно найти модуль равнодействующей силы на объект.

Как найти модуль равнодействующих сил по векторам

Если имеется только два вектора сил, их равнодействующая сила может быть найдена с помощью правила параллелограмма. Сначала нужно наложить векторы сил друг на друга так, чтобы их начало было в одной точке. Затем проведите прямую через концы векторов. Вектор, идущий от начала до конца этой прямой, будет представлять равнодействующую силу. Чтобы найти модуль равнодействующей силы, измерьте длину этого вектора.

Если у вас есть несколько векторов сил, их равнодействующая сила может быть найдена путем сложения векторов. Для этого нужно сложить все векторы сил по отдельности и получить итоговый вектор. Затем, чтобы найти модуль равнодействующей силы, измерьте длину этого вектора.

Найти модуль равнодействующих сил по векторам важно для понимания, сколько общей силы действует на объект. Это может быть полезно при решении задач механики, динамики или статики, а также при определении равновесия объекта.

Определение и методы нахождения модуля равнодействующих сил

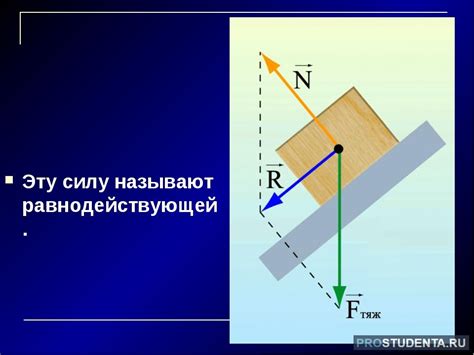
Модуль равнодействующих сил представляет собой величину, которая определяет суммарную силу, действующую на объект в определенном направлении. Благодаря данной величине мы можем определить, как силы, действующие на объект, влияют на его движение или состояние покоя.

Существует несколько методов для нахождения модуля равнодействующих сил:

1. Метод графической композиции векторов. Согласно данному методу, силы представляются векторами, а модуль равнодействующих сил определяется по результатам графического сложения сил. Для этого необходимо построить векторы сил в масштабе, а затем применить соответствующие правила сложения векторов.
2. Метод разложения векторов на составляющие. Этот метод основан на представлении каждой силы в виде двух взаимно перпендикулярных направлений (обычно горизонтального и вертикального). После разложения векторов на составляющие, модуль равнодействующих сил определяется как гипотенуза прямоугольного треугольника, образованного составляющими.
3. Метод аналитической геометрии. С помощью данного метода силы представляются в виде уравнений. Путем алгебраических операций можно найти модуль равнодействующих сил.

Выбор метода нахождения модуля равнодействующих сил зависит от конкретной задачи и доступных данных о силах, действующих на объект. Знание таких методов позволяет определить и предсказать последствия воздействия сил на объекты.

Пример решения задачи на определение модуля равнодействующих сил по векторам

Рассмотрим задачу, в которой имеются две силы, направленные в разные стороны.

Пусть у нас имеются две силы: F1, действующая в направлении А, и F2, действующая в направлении В. Нам нужно найти модуль равнодействующих этих сил по векторам.

Для начала определим векторы F1 и F2. Представим эти векторы в виде направленных отрезков, причем началом обоих отрезков является начало координат. Затем проведем векторную сумму векторов F1 и F2, то есть соединим конец отрезка, представляющего вектор F1, с концом отрезка, представляющего вектор F2.

Далее, используя геометрический метод, проведем отрезок, соединяющий начало и конец вектора, представляющего модуль равнодействующих сил. Обозначим его как v.

Теперь, с помощью измерительного инструмента, определим длину отрезка v. Эта длина и будет являться модулем равнодействующих сил по векторам.

Итак, в данной задаче модуль равнодействующих сил по векторам равен длине отрезка v, который является векторной суммой векторов F1 и F2.

Таким образом, мы можем определить модуль равнодействующих сил, используя геометрический метод и измерительный инструмент.

Виды задач на поиск модуля равнодействующих сил по векторам

1. Задачи на равновесие тела. В данном случае, модуль равнодействующих сил должен быть равен нулю, чтобы тело находилось в состоянии равновесия.
2. Задачи на движение тела при действии нескольких сил. В этой категории задач, модуль равнодействующих сил позволяет определить силу, которая будет ответственна за движение тела.
3. Задачи на вычисление ускорения тела. Здесь модуль равнодействующих сил используется для определения ускорения тела в заданном направлении.
4. Задачи на вычисление силы трения. В данном случае, модуль равнодействующих сил поможет определить силу трения, которая будет препятствовать движению тела.
5. Задачи на составление силовых треугольников. Здесь модуль равнодействующих сил позволяет построить силовой треугольник и определить модуль суммарной силы.

Каждый вид задач требует определенного подхода к вычислению модуля равнодействующих сил по векторам. Понимание этих различных ситуаций позволяет решать задачи более эффективно и получать точные результаты.