В математике 6 класса одной из важных тем является нахождение наименьшего общего кратного, или НОК (Н.О.К.), двух или более чисел. НОК является результатом перемножения чисел, учитывая их общие множители и уникальные множители. Знание и умение применять правила нахождения НОК поможет школьникам решать задачи, связанные с дробями, разделением предметов на равные группы и другими математическими проблемами.
В основе правил нахождения НОК лежат знания о разложении чисел на простые множители. Чтобы найти НОК двух чисел, необходимо разложить их на простые множители и перемножить эти множители, учитывая их кратность. Если некоторые множители встречаются у обоих чисел, то их кратность также учитывается.
Для нахождения НОК необходимо выполнить следующие шаги:
- Разложить каждое число на простые множители.
- Выбрать все простые множители с их максимальной кратностью.
- Умножить выбранные простые множители вместе.
Рассмотрим пример нахождения НОК для чисел 12 и 18. Разложим каждое число на простые множители:
12 = 2 × 2 × 3
18 = 2 × 3 × 3
Выберем все простые множители с их максимальной кратностью:
2 × 2 × 3 × 3 = 36
Таким образом, НОК чисел 12 и 18 равен 36.
Определение понятия НОК в математике
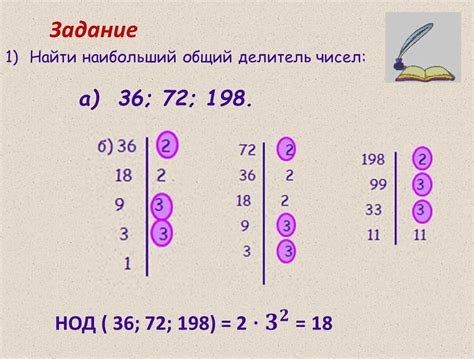
Другими словами, НОК двух или более чисел - это наименьшее число, которое является кратным всем данным числам.
Чтобы найти НОК, нужно просмотреть все кратные числа до достижения чисел, для которых ищется НОК, и найти наименьшее общее число, удовлетворяющее условию. НОК можно вычислить с помощью разложения чисел на простые множители и выбора максимальных степеней простых множителей.
Например, для чисел 12 и 16:
12 = 22 * 3
16 = 24
НОК(12, 16) = 24 * 3 = 48
То есть, НОК(12, 16) равно числу 48, так как 48 делится нацело на оба числа - 12 и 16.
Правила вычисления НОК и его свойства
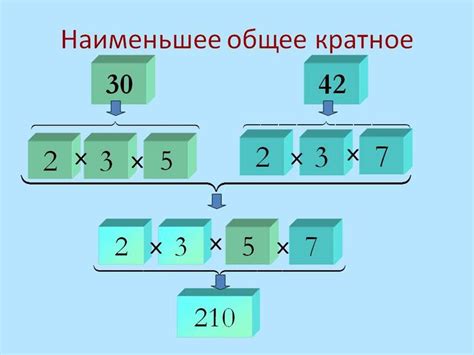
Вот основные правила вычисления НОК:
- Для вычисления НОК двух чисел нужно найти их общие делители и выбрать наименьшее общее кратное.
- Если числа простые, то НОК будет равно их произведению.
- Если числа имеют общие множители, то они вносятся в НОК только один раз.
- Если числа имеют разные простые множители, то каждый множитель с наибольшей степенью вносится в НОК.
Из свойств НОК можно выделить следующие:
- НОК всегда больше или равен исходным числам.
- Если два числа равны, то их НОК также будет равен этим числам.
- Максимальное значение НОК двух чисел равно их произведению.
- Если число делится нацело на другое, то его НОК с этим числом будет равен этому числу.
Правила вычисления НОК и его свойства помогают решать задачи, связанные с различными арифметическими операциями и комбинаторикой. Понимание этих правил и свойств поможет учащимся успешно справляться с заданиями и улучшит их математическое мышление.
Примеры расчета НОК в математике 6 класс

Для того чтобы найти НОК (наименьшее общее кратное) двух чисел, нужно выполнить следующие шаги:
Пример 1:
| Число | 2 | 3 | 5 |
|---|---|---|---|
| Число, кратное 2 | 2 | 6 | 10 |
| Число, кратное 3 | 6 | 6 | 15 |
| Число, кратное 5 | 10 | 15 | 15 |
Из таблицы видно, что наименьшее общее кратное (НОК) чисел 2, 3 и 5 равно 30.
Пример 2:
| Число | 4 | 6 | 8 |
|---|---|---|---|
| Число, кратное 4 | 4 | 12 | 16 |
| Число, кратное 6 | 12 | 6 | 24 |
| Число, кратное 8 | 16 | 24 | 8 |
Из таблицы видно, что наименьшее общее кратное (НОК) чисел 4, 6 и 8 равно 24.
Пример 3:
| Число | 5 | 9 | 15 |
|---|---|---|---|
| Число, кратное 5 | 5 | 45 | 75 |
| Число, кратное 9 | 45 | 9 | 45 |
| Число, кратное 15 | 75 | 45 | 15 |
Из таблицы видно, что наименьшее общее кратное (НОК) чисел 5, 9 и 15 равно 45.