Дроби - это числа, которые состоят из числителя и знаменателя, разделенных чертой. Часть дроби - это число, которое является результатом деления числителя на знаменатель. На первый взгляд может показаться, что нахождение части дроби сложно, но на самом деле это довольно просто, если знать несколько правил и следовать определенным шагам.
Первым шагом для нахождения части дроби является выделение целой части. Если числитель больше знаменателя, то можно узнать целую часть дроби, разделив числитель на знаменатель. Например, дробь 7/4 имеет целую часть 1, так как 7 делится на 4 один раз с остатком 3.
Вторым шагом является определение остатка. Если числитель больше знаменателя, остаток можно найти путем вычитания произведения целой части на знаменатель из числителя. Таким образом, для дроби 7/4, остаток равен 3.
Наконец, чтобы найти часть дроби, нужно разделить остаток на знаменатель. Полученное число и будет являться частью дроби. В примере с дробью 7/4, остаток 3 делится на знаменатель 4, и получается часть дроби 3/4.
Зачем нужно найти часть дроби?

| 1. | Вычисление десятичного представления дроби. |
| 2. | Сравнение и упорядочивание дробей. |
| 3. | Построение числовых примеров и задач. |
| 4. | Решение уравнений и неравенств, включающих дроби. |
Нахождение части дроби также помогает визуализировать дробь на числовой оси и лучше понять её положение и значение в отношении других чисел. Изучение этого процесса способствует развитию навыков аналитического мышления и обобщенной математической компетенции.
Примеры задач, в которых требуется найти часть дроби

Задачи, которые требуют нахождения части дроби, могут возникнуть в различных контекстах. Вот несколько примеров таких задач:
Пример 1:
У Васи было 8 конфет. Он съел часть из них и отдал 3 своим друзьям. Каждому другу досталось по 1 конфете. Какая часть конфет осталась у Васи?
Решение:
У Васи было 8 конфет. Он отдал 3 конфеты, так что осталось 8 - 3 = 5 конфет. Каждому другу досталась по 1 конфете, так что они вместе получили 1 * 3 = 3 конфеты. Итак, у Васи осталось 5 - 3 = 2 конфеты. Чтобы найти часть дроби, нужно найти отношение оставшихся конфет к исходному количеству конфет: 2 / 8 = 1 / 4. Так что, у Васи осталась 1/4 часть конфет.
Пример 2:
Аня купила 10 яблок и раздала часть из них своим друзьям. У каждого друга было по 2 яблока. Какая часть яблок осталась у Ани?
Решение:
У Ани было 10 яблок. Каждому другу досталось по 2 яблока, так что они вместе получили 2 * 3 = 6 яблок. Итак, у Ани осталось 10 - 6 = 4 яблока. Чтобы найти часть дроби, нужно найти отношение оставшихся яблок к исходному количеству яблок: 4 / 10 = 2 / 5. Так что, у Ани осталась 2/5 часть яблок.
Пример 3:
На столе лежало 12 книг, а Иван поместил на полку 3/4 части от них. Сколько книг осталось на столе?
Решение:
На столе лежало 12 книг. Иван положил на полку 3/4 части от них, что составляет 3/4 * 12 = 9 книг. Итак, на полку было переложено 9 книг, поэтому на столе осталось 12 - 9 = 3 книги. Таким образом, на столе осталось 3 книги.
Это лишь несколько примеров задач, которые требуют нахождения части дроби. При решении таких задач необходимо использовать основные правила умножения и деления дробей. Такие упражнения помогут развить навыки работы с дробями и понимание их природы.
Шаг 1: Определите числитель и знаменатель

Например, в дроби 3/4, число 3 является числителем, а число 4 - знаменателем.
Числитель указывает, сколько частей выбрано из целого, а знаменатель определяет количество одинаковых частей, на которые разделено целое.
Для некоторых дробей числитель может быть равен нулю, что означает, что выбрано ноль частей из целого. Знаменатель также может быть нулевым, но в данном случае дробь не существует.
Таким образом, определение числителя и знаменателя является первым шагом к нахождению части дроби.
Шаг 2: Сократите дробь, если это возможно

Чтобы сократить дробь, найдите общие делители числителя и знаменателя, а затем разделите их на наибольший общий делитель (НОД).
Например, для дроби 8/12 мы можем найти общие делители чисел 8 и 12: 1, 2 и 4. Наибольший общий делитель равен 4, поэтому сокращенная форма дроби будет 2/3.
Сокращение дробей позволяет упростить вычисления и получить более понятные результаты. Кроме того, сокращенная дробь может быть более удобной для использования в других математических операциях.
Помните: не все дроби можно сократить. Если числитель и знаменатель не имеют общих делителей, или их наибольший общий делитель равен 1, то дробь уже находится в наиболее простой форме и ее невозможно сократить.
Примечание: в некоторых случаях дробь может быть сразу представлена в упрощенной форме или числитель и знаменатель могут быть пропорциональны. В таких случаях сокращение дроби не требуется.
Шаг 3: Выделите нужную часть дроби
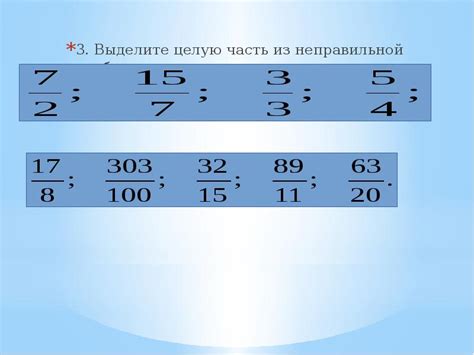
Существуют различные виды дробей, и каждая из них требует определенного подхода для нахождения нужной части. Вот несколько основных правил:
- Правильные дроби: дроби, в которых числитель меньше знаменателя. Чтобы найти нужную часть такой дроби, достаточно разделить числитель на знаменатель и умножить результат на нужное количество частей.
- Неправильные дроби: дроби, в которых числитель больше знаменателя. Для нахождения нужной части такой дроби можно использовать ту же формулу, но сначала нужно выделить целую часть. Для этого необходимо разделить числитель на знаменатель, получить целую часть и остаток. Затем нужно умножить остаток на нужное количество частей.
- Смешанные числа: числа, которые представляют собой комбинацию целой части и дробной части (неправильной дроби). Чтобы выделить нужную часть смешанного числа, необходимо сложить целую часть с результатом умножения остатка на нужное количество частей.
Эти правила помогут вам выделить нужную часть дроби и решать задачи, связанные с дробями. Запомните их и применяйте в практике для успешного решения задач!
Шаг 4: Приведите полученную дробь к наименьшим частям

После выполнения предыдущих шагов, у вас получится десятичная дробь, которую нужно представить в виде обыкновенной дроби. Для этого необходимо сократить полученную дробь до наименьших частей.
Для сокращения дроби нужно найти наибольший общий делитель числителя и знаменателя. Общие делители чисел можно найти, разложив их на простые множители и сравнив их степени. Наибольший общий делитель можно определить по самым высоким степеням простых чисел, которые входят в разложение чисел.
Приведем пример:
| Дробь | Числитель | Знаменатель |
| 0.8 | 8 | 10 |
Разложим числитель и знаменатель на простые множители:
| Числитель | Знаменатель |
| 8 = 2 * 2 * 2 | 10 = 2 * 5 |
Найдем наибольший общий делитель:
| Делители числителя | Делители знаменателя | Наибольший общий делитель |
| 2, 2, 2 | 2, 5 | 2 |
Чтобы сократить дробь, необходимо разделить числитель и знаменатель на их наибольший общий делитель:
| Новая дробь | Новый числитель | Новый знаменатель |
| 0.8 = 8/10 | 8 / 2 | 10 / 2 |
| 4 | 5 |
Таким образом, исходная десятичная дробь 0.8 была приведена к обыкновенной дроби 4/5, которая не может быть дальше упрощена и является наименьшими частями.
Правила нахождения части дроби с несколькими знаменателями
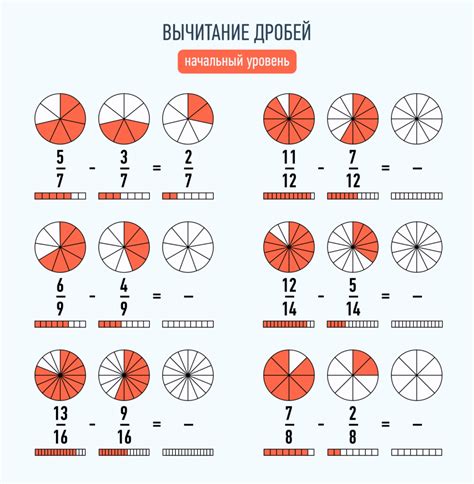
Нахождение части дроби с несколькими знаменателями может быть немного сложнее, чем с одним знаменателем. Однако следуя нескольким простым правилам, можно успешно решить такие задачи.
1. Изучите знаменатели дробей. Если знаменатели всех дробей одинаковы, то вам повезло - ситуация стандартная. Если же знаменатели разные, перейдите к следующему шагу.
2. Найдите наименьшее общее кратное (НОК) всех знаменателей. Он понадобится вам для приведения знаменателей к общему знаменателю.
3. Приведите все дроби к общему знаменателю. Для этого умножьте каждую дробь на такое число, чтобы ее знаменатель стал равным общему знаменателю.
4. Решите полученное уравнение с общим знаменателем. Для этого сложите (или вычтите) числители полученных дробей, оставив знаменатель без изменений.
5. Упростите полученную дробь, если это возможно. Для этого найдите общий делитель числителя и знаменателя и поделите их на этот делитель.
Применяя эти правила, вы сможете успешно находить часть дроби с несколькими знаменателями, даже если задача на первый взгляд кажется сложной. Практика и обучение помогут вам улучшить навыки решения таких задач.
Примеры решения задач на нахождение части дроби
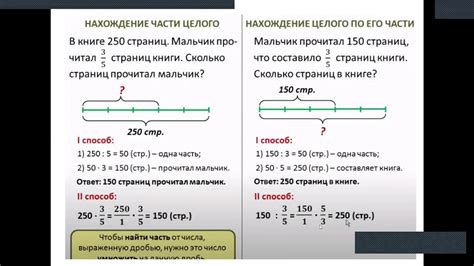
Решение задач на нахождение части дроби в математике может показаться сложным, но с помощью правильных шагов и правил, вы сможете легко справиться с ними. Вот несколько примеров, чтобы помочь вам понять процесс нахождения части дроби:
Пример 1:
Задача: Найдите 1/4 от числа 36.
Шаг 1: Умножьте числитель дроби на число.
1/4 * 36 = 36/4.
Шаг 2: Упростите дробь, если это возможно.
36/4 = 9.
Ответ: 1/4 от числа 36 равно 9.
Пример 2:
Задача: Найдите 3/5 от числа 55.
Шаг 1: Умножьте числитель дроби на число.
3/5 * 55 = 165/5.
Шаг 2: Упростите дробь, если это возможно.
165/5 = 33.
Ответ: 3/5 от числа 55 равно 33.
Пример 3:
Задача: Найдите 2/3 от числа 90.
Шаг 1: Умножьте числитель дроби на число.
2/3 * 90 = 180/3.
Шаг 2: Упростите дробь, если это возможно.
180/3 = 60.
Ответ: 2/3 от числа 90 равно 60.
Запомните эти шаги и пройдите несколько упражнений, чтобы улучшить свои навыки в нахождении части дробей. Со временем вы станете более опытным и уверенным в решении таких задач.