Нахождение наименьшего общего кратного (НОК) дробей с разными знаменателями является важной задачей в математике. НОК позволяет упростить дроби и делать с ними различные операции, такие как сложение, вычитание, умножение и деление. Существует несколько способов и алгоритмов, которые помогают найти НОК дробей без особых усилий.
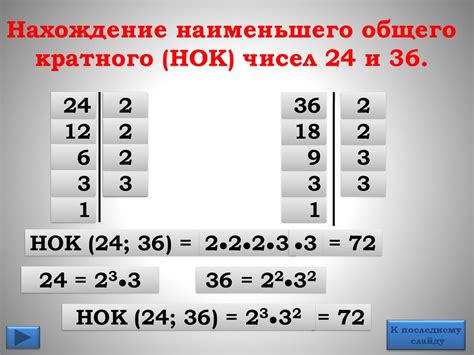
Один из способов нахождения НОК дробей - это разложение каждого знаменателя на простые множители и выбор максимальной степени простого числа. Например, если у нас есть дроби 1/3 и 1/4, мы можем разложить числа 3 и 4 на простые множители: 3 = 3^1 и 4 = 2^2. Далее, мы выбираем максимальные степени простых чисел: 3^1 и 2^2, и перемножаем их: 3^1 * 2^2 = 12. Таким образом, НОК дробей 1/3 и 1/4 равен 12.
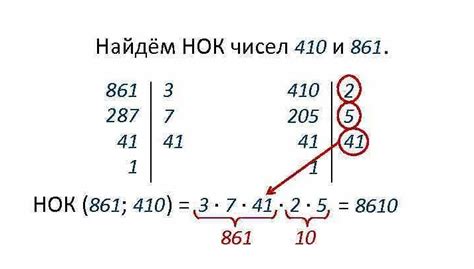
Другой способ нахождения НОК дробей - использование алгоритма Евклида. Для этого мы должны найти НОД (наибольший общий делитель) знаменателей дробей и затем разделить их на НОД. Например, если у нас есть дроби 2/5 и 3/7, мы находим НОД чисел 5 и 7: 5 и 7 не имеют общих делителей, кроме 1, поэтому НОД равен 1. Затем мы делим произведение знаменателей на НОД: 5 * 7 / 1 = 35. Таким образом, НОК дробей 2/5 и 3/7 равен 35.
Что такое НОК?
НОК используется для решения различных задач, особенно в математике и алгоритмах. В контексте нахождения НОК дробей с разными знаменателями, НОК позволяет найти наименьшее число, которое является общим знаменателем для всех дробей. Это особенно полезно при работе с дробями, так как позволяет выполнять операции сложения, вычитания и умножения с минимальными преобразованиями дробей.
Существуют различные способы и алгоритмы нахождения НОК, такие как поиск простых множителей, метод простых множителей или использование таблицы НОК. Каждый из них имеет свои преимущества и недостатки в зависимости от конкретной задачи и доступных ресурсов.
Важно понимать, что НОК уникален для каждой пары чисел и может быть использован для определения эквивалентности дробей. Поэтому знание понятия НОК и способов его нахождения является необходимым для решения задач, связанных с дробями и их операциями.
Определение и смысл термина

Знаменатель дроби в математике указывает, на какое количество равных частей разделено целое число. Если знаменатели дробей разные, для выполнения действий с этими дробями необходимо найти общий знаменатель, чтобы можно было сложить, вычесть, умножить или делить их.
Определение НОК позволяет найти и использовать такой общий знаменатель для выполнения арифметических операций над дробями с разными знаменателями. Таким образом, НОК оказывается полезной концепцией при работе с дробными числами и помогает в решении различных математических задач и задач реального мира.
Зачем нужно находить НОК дробей?

Одной из главных целей нахождения НОК является выполнение операций сложения и вычитания дробей. Для выполнения этих операций, знаменатели дробей должны быть равными или кратными друг другу. НОК позволяет нам установить такие общие знаменатели, тем самым позволяя нам сложить или вычесть дроби.
Важной областью, где нахождение НОК необходимо, является работа с дробными числами в арифметических и математических задачах. Например, когда необходимо найти общее время выполнения различных операций или общую долю, которую занимает каждая дробь в общей сумме.
Также, нахождение НОК может быть полезным при упрощении и сравнении дробей. Нахождение НОК позволяет нам привести дроби к общему знаменателю, что упрощает их сравнение и определение, какая из них больше или меньше.
Итак, нахождение НОК дробей играет важную роль в решении множества задач и проблем, связанных с дробными числами и их операциями. Этот шаг позволяет нам объединить дроби с разными знаменателями в единую дробь, упрощает их сравнение, арифметические операции, а также облегчает работу с дробными числами в различных математических и арифметических задачах.
Первый способ: разложение на произведение простых множителей

Первый способ нахождения наименьшего общего кратного (НОК) двух дробей с разными знаменателями основан на разложении знаменателей этих дробей на простые множители.
Для начала разлагаем знаменатели дробей на простые множители. Затем выбираем все простые множители, которые встречаются в разложениях этих знаменателей. Для каждого простого множителя выбираем наибольшую его степень, которая встречается среди всех дробей.
Следующим шагом находим произведение всех выбранных простых множителей, возведенных в соответствующие степени. Это и будет НОК данных дробей.
Приведенный метод позволяет найти НОК дробей с разными знаменателями без необходимости нахождения их общего знаменателя. Кроме того, этот способ эффективен при работе с дробями, состоящими из больших чисел.
Второй способ: использование алгоритма Евклида
Для применения алгоритма Евклида к дробям с разными знаменателями, сначала нужно найти НОД их знаменателей. Затем НОК будет равен произведению знаменателей, деленному на НОД.
Приведем пример. Пусть у нас есть две дроби: 2/3 и 5/8. Для начала найдем НОД знаменателей.
| Дроби | Знаменатели | НОД |
|---|---|---|
| 2/3 | 3 | |
| 5/8 | 8 |
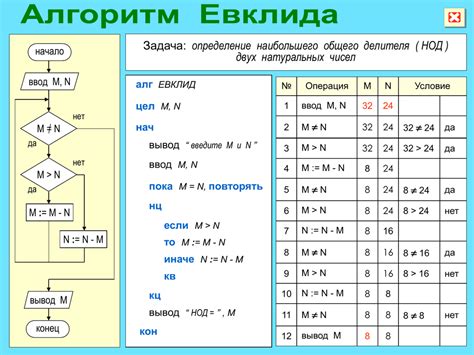
Для нахождения НОД знаменателей можно использовать алгоритм Евклида следующим образом:
1. Делим большее число на меньшее. 2. Если остаток от деления равен 0, то меньшее число является НОД. 3. Если остаток от деления не равен 0, то заменяем большее число на меньшее, а остаток на большее число, и повторяем шаг 1.
Применим этот алгоритм к числам 3 и 8:
Шаг 1: 8 / 3 = 2 (остаток 2) Шаг 2: 3 / 2 = 1 (остаток 1) Шаг 3: 2 / 1 = 2 (остаток 0)
Таким образом, НОД(3, 8) = 1.
Теперь, чтобы найти НОК дробей 2/3 и 5/8, мы умножим их знаменатели и разделим на НОД(3, 8):
НОК(2/3, 5/8) = (3 * 8) / 1 = 24.
Таким образом, НОК дробей 2/3 и 5/8 равен 24. Это означает, что наименьшее общее кратное этих дробей будет равно 24.
Третий способ: использование таблицы умножения

Для использования этого метода, мы будем работать с знаменателями наших дробей. Перечислим все числа, начиная с 2 и до наибольшего знаменателя. Затем составим таблицу умножения из этих чисел, с каждым числом умножив все числа в таблице. Затем будем искать наименьшее число в таблице, которое делится на все знаменатели без остатка.
| 2 | 3 | 4 | 5 | |
|---|---|---|---|---|
| 2 | 4 | 6 | 8 | 10 |
| 3 | 6 | 9 | 12 | 15 |
| 4 | 8 | 12 | 16 | 20 |
| 5 | 10 | 15 | 20 | 25 |
В этой таблице мы можем заметить, что наименьшее число, которое делится на все знаменатели без остатка, равно 20. Следовательно, нашим НОК будет 20.
Таким образом, используя таблицу умножения, мы можем быстро и эффективно найти НОК для дробей с разными знаменателями.
Как проверить правильность найденного НОК?
Найденное наименьшее общее кратное (НОК) двух или более дробей с разными знаменателями можно проверить на правильность с помощью нескольких простых шагов:
- Умножьте каждую из исходных дробей на число, равное НОК знаменателей. После этого все дроби будут иметь одинаковые знаменатели и можно будет сравнить числители.
- Проверьте, являются ли числители всех дробей равными. Если все числители одинаковые, то найденный НОК является правильным. В этом случае НОК можно считать окончательным результатом.
- Если числители различаются, значит, найденное НОК не является правильным. В таком случае следует продолжить поиск и повторить алгоритм для более крупных чисел.
Проверка правильности найденного НОК позволяет убедиться, что используемый алгоритм дает верные результаты и можно быть уверенным в том, что НОК найден корректно.
Примеры решения задач по нахождению НОК дробей
НОК дробей с разными знаменателями можно найти различными способами. Рассмотрим несколько примеров, чтобы лучше понять процесс решения таких задач.
Пример 1:
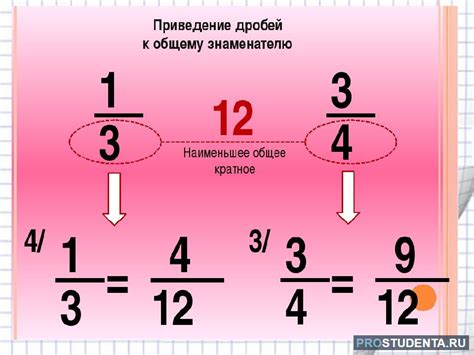
Найти НОК дробей 2/3 и 3/4.
Решение:
- Запишем знаменатели дробей: 3 и 4.
- Найдем их НОК. Разложим числа на простые множители: 3 = 3 и 4 = 2 * 2.
- НОК будет равен произведению всех простых множителей с наибольшей степенью в разложении: НОК(3, 4) = 2 * 2 * 3 = 12.
Ответ: НОК дробей 2/3 и 3/4 равен 12.
Пример 2:
Найти НОК дробей 1/5 и 2/7.
Решение:
- Запишем знаменатели дробей: 5 и 7.
- Найдем их НОК. Разложим числа на простые множители: 5 = 5 и 7 = 7.
- НОК будет равен произведению всех простых множителей с наибольшей степенью в разложении: НОК(5, 7) = 5 * 7 = 35.
Ответ: НОК дробей 1/5 и 2/7 равен 35.
Пример 3:
Найти НОК дробей 2/9, 3/8 и 4/5.
Решение:
- Запишем знаменатели дробей: 9, 8 и 5.
- Найдем их НОК. Разложим числа на простые множители: 9 = 3 * 3, 8 = 2 * 2 * 2 и 5 = 5.
- НОК будет равен произведению всех простых множителей с наибольшей степенью в разложении: НОК(9, 8, 5) = 2 * 2 * 2 * 3 * 3 * 5 = 360.
Ответ: НОК дробей 2/9, 3/8 и 4/5 равен 360.
Таким образом, для нахождения НОК дробей с разными знаменателями нужно разложить знаменатели на простые множители и записать их НОК как произведение всех простых множителей с наибольшей степенью в разложении.