Поиск нулей функции - важная задача в математике и науках, связанных с анализом и моделированием данных. Нуль функции, или корень уравнения, представляет собой значение аргумента, при котором функция обращается в ноль. Нахождение нулей функции может быть полезным для определения точек пересечения графика с осью абсцисс, а также для решения уравнений.
В этой статье мы рассмотрим пошаговое руководство по поиску нулей функции. Во-первых, мы ознакомимся с основными понятиями, связанными с нулями функции, включая понятие корня уравнения и способы их поиска. Далее, мы рассмотрим различные методы численного и аналитического поиска нулей функции, включая метод половинного деления, метод Ньютона и метод простых итераций. Кроме того, мы научимся использовать программные инструменты, такие как математические пакеты и компьютерные программы, для нахождения нулей функции.
Итак, если вы хотите научиться находить нули функции, полезных для решения различных задач и проблем, то это руководство вам поможет. Следуйте инструкциям и упражняйтесь на различных примерах, чтобы на практике освоить методы поиска нулей функции. Поехали!
Зачем нужно найти нули функции?

В теории функций нули позволяют определить особые точки, такие как экстремумы или точки перегиба, а также позволяют анализировать поведение функции на интервалах ил заданном отрезке. Нули функции служат основой для сравнительного анализа различных функций, и могут использоваться для доказательства существования распределения.
В практических задачах, нахождение нулей функции является необходимым для решения уравнений, определения точек пересечения графиков функций, а также для нахождения критических значений и минимумов/максимумов функций при определенных условиях. Это особенно полезно в финансовых, инженерных и научных областях, где точность и предсказуемость значительно важны.
В общем, нахождение нулей функции помогает нам получить ценную информацию о ее поведении и характеристиках, а также использовать ее для решения различных теоретических и практических задач.
Важное предупреждение перед началом поиска
Перед тем, как начать поиск нулей функции, необходимо убедиться в том, что функция имеет непрерывный график на интервале, на котором вы планируете искать нули. Если функция имеет разрывы или вертикальные асимптоты на данном интервале, то методы поиска нулей, которые будут рассмотрены далее, могут не сработать.
Также важно отметить, что аналитическое решение уравнения f(x) = 0 может быть невозможно или чрезвычайно сложным, поэтому в некоторых случаях приходится прибегать к численным методам для поиска приближенного значения нуля функции.
В процессе поиска нулей функции необходимо быть внимательным и аккуратным, тщательно следить за последовательностью выполнения шагов и сохранять промежуточные результаты. Ошибки в расчетах или пропущенные шаги могут привести к некорректному результату.
В следующих разделах будут рассмотрены различные методы поиска нулей функции, начиная с простых и до более сложных. Выбор метода будет зависеть от характера функции и доступных ресурсов для вычислений.
Шаг 1: Выразить функцию в виде уравнения

Прежде чем начать поиск нулей функции, необходимо выразить ее в виде уравнения. Уравнение функции представляет собой выражение, где функция приравнивается к нулю.
Например, пусть дана функция f(x) = 2x^2 - 5x + 3. Чтобы выразить эту функцию в виде уравнения, необходимо приравнять ее к нулю:
2x^2 - 5x + 3 = 0
Теперь функцию можно рассматривать как уравнение и начинать процесс поиска ее нулей.
Шаг 2: Построить график функции
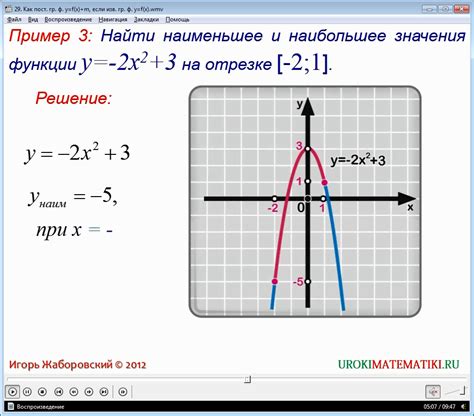
Построение графика функции предоставляет визуальное представление ее поведения и помогает найти нули функции. Чтобы построить график, нужно выполнить следующие шаги:
1. Определить область определения функции:
Проанализируйте функцию и определите, в каких точках она не определена (например, деление на ноль или извлечение корня из отрицательного числа).
2. Определить поведение функции:
Исследуйте функцию и определите, как она ведет себя при изменении значения аргумента. Определите, есть ли особые точки (вершины, асимптоты, точки разрыва).
3. Определить интервалы значений аргумента:
Разбейте область определения функции на интервалы, чтобы определить, где она может иметь нули. Выберите начальные значения для каждого интервала.
4. Построить оси координат:
Нарисуйте горизонтальную ось (ось абсцисс) и вертикальную ось (ось ординат) на вашей декартовой системе координат.
5. Построить график функции:
Используйте выбранные значения аргумента для каждого интервала и найдите соответствующие значения функции. Соедините полученные точки на графике. При необходимости, используйте компьютерные программы или графические калькуляторы для построения графика.
Заметка: Построение графика может требовать некоторой творческой интерпретации и оценки. Более подробные инструкции будут зависеть от конкретной функции, которую вы исследуете.
Шаг 3: Определить интервалы, на которых есть нули функции

Чтобы найти нули функции, необходимо определить интервалы, на которых функция меняет знак с плюса на минус или с минуса на плюс. Эти интервалы будут содержать нули функции.
Для определения таких интервалов необходимо проанализировать значения функции в различных точках внутри области определения. Запишите значения функции для некоторых значений аргумента и определите, как меняется знак.
Например, если значения функции при аргументе 0 и 1 являются положительными, а при аргументе 2 - отрицательным, то на интервале от 1 до 2 функция меняет знак с плюса на минус и, следовательно, имеет нуль в этом интервале.
Повторите этот процесс для всех значений аргумента, пока не найдете все интервалы, на которых у функции есть нули.
Шаг 4: Применить метод половинного деления
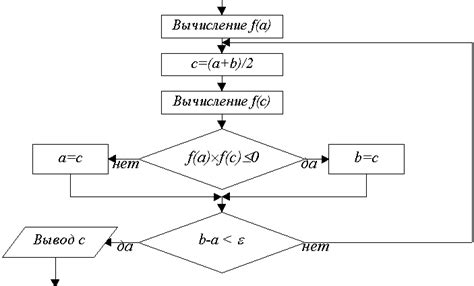
Для применения метода половинного деления, необходимо иметь начальные значения интервала, в котором находятся нули функции. Начальный интервал выбирается таким образом, чтобы на его концах функция принимала значения с разными знаками.
В начале метода половинного деления, определяется середина интервала. Затем проверяется знак функции в этой точке. Если знак совпадает с знаком на одном из концов интервала, то середина интервала становится новым концом. Если знак не совпадает, то середина интервала становится новой серединой.
Процесс деления интервала пополам и проверки знаков продолжается до тех пор, пока длина интервала не станет меньше заданной точности. Как только достигнута заданная точность, точка, в которой функция обращается в ноль, считается найденной.
Метод половинного деления является достаточно простым и надежным способом нахождения нулей функции. Однако, он может потребовать большого количества итераций, особенно для функций с особо сложным поведением.
Шаг 5: Проверить найденные нули функции
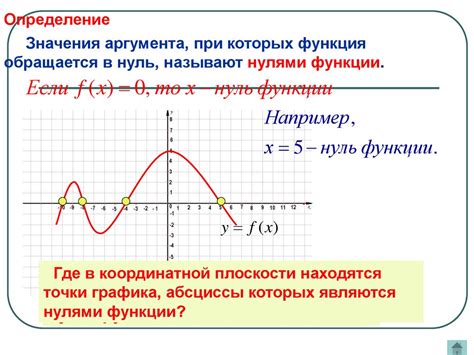
После того, как мы нашли нули функции, необходимо проверить их корректность. Для этого мы можем использовать несколько методов.
- Подставить найденные нули функции в исходное выражение и убедиться, что оно равно нулю.
- Построить график функции и убедиться, что нашли точки, в которых график пересекает ось абсцисс.
- Рассчитать производную функции и убедиться, что найденные нули являются ее корнями.
Если все методы подтверждают, что найденные значения являются нулями функции, то мы можем быть уверены в их правильности. В противном случае, мы должны вернуться к предыдущим шагам и повторить процесс поиска нулей. При этом также может потребоваться использование более точных методов, например, метода Ньютона или метода деления отрезка пополам.
Шаг 6: Повторить шаги 4-5, если нужно
Помните, что процесс нахождения нулей функции может потребовать нескольких итераций, особенно если функция сложная или содержит много переменных. Также не забывайте про возможные ошибки вычислений или округления, которые могут повлиять на результаты.
Повторять шаги 4 и 5 по мере необходимости позволит вам находить все действительные нули функции и получить более точное представление о ее поведении. Не бойтесь экспериментировать и проверять разные значения, чтобы получить наилучший результат.