Определение объема является важным аспектом в различных областях науки и инженерии. Независимо от того, строите ли вы дом, проектируете новое изобретение или решаете математическую задачу, рассчитать объем объекта может оказаться необходимым. Знание методов расчета объема позволяет оценить размеры и вместимость объекта без его физического измерения.
Одним из простейших способов вычисления объема является использование формулы, которая связывает площадь основания и высоту объекта. Например, для прямоугольного параллелепипеда объем можно вычислить, умножив площадь основания на высоту. Этот принцип применим не только к прямоугольным, но и к другим геометрическим формам, таким как цилиндр, конус или шар.
Для более сложных форм объектов существуют различные математические формулы, позволяющие вычислить объем. Например, для куба формула простая: объем равен трехмерному измерению одного его ребра, возведенному в куб. Однако существуют и более сложные формулы для объектов, состоящих из нескольких геометрических фигур или имеющих специфическую структуру.
Что такое объем
Объем можно представить как количество пространства, занимаемого телом или фигурой. Он измеряется в кубических единицах, таких как кубический метр (м³) или кубический сантиметр (см³).
Объем можно вычислить различными способами, в зависимости от формы объекта. Для некоторых фигур, таких как прямоугольные параллелепипеды или кубы, объем можно вычислить, умножив площадь основы на высоту. Для других фигур, таких как сферы или цилиндры, существуют специальные формулы.
Понимание понятия объема важно во многих областях, включая строительство, архитектуру, инженерию, физику и химию. Расчет объема позволяет оценить необходимое количество материалов, пространство для хранения или владение объемом жидкости или газа.
Определение понятия "объем"

Объем можно вычислить для различных геометрических фигур, таких как кубы, параллелепипеды, цилиндры и шары. Для каждой фигуры существуют соответствующие формулы, которые позволяют вычислить ее объем.
Наиболее простой способ вычисления объема - использование формулы, которая учитывает площадь основания и высоту фигуры. Например, для прямоугольного параллелепипеда формула будет следующей:
| Фигура | Формула для вычисления объема |
|---|---|
| Прямоугольный параллелепипед | объем = площадь основания × высота |
| Цилиндр | объем = площадь основания × высота |
| Шар | объем = (4/3) × π × радиус³ |
Вычисление объема позволяет определить, сколько материала необходимо для создания объекта или сколько жидкости может содержать сосуд. Понимание понятия "объем" является важным в физике, архитектуре, строительстве и других научных и технических областях.
Значение объема в геометрии

Объем может быть вычислен для различных геометрических фигур, таких как куб, параллелепипед, цилиндр, конус, шар и др. Для каждой фигуры существует своя формула вычисления объема, основанная на ее особенностях и геометрических свойствах.
Знание значения объема в геометрии позволяет решать различные практические задачи, связанные с измерениями и расчетами. Например, вычисление объема жидкости в емкости, определение вместимости контейнера или рассчет объема материала для строительства.
Помимо этого, понимание значения объема в геометрии помогает визуализировать и представить трехмерные объекты и их взаимное расположение в пространстве. Знание объема позволяет анализировать и сравнивать фигуры, а также моделировать и строить новые объекты.
В итоге, значение объема в геометрии играет ключевую роль в понимании и работе с трехмерными пространственными объектами, а также в решении практических задач из различных областей науки и техники.
Формула для вычисления объема
Для вычисления объема объекта необходимо использовать соответствующую формулу, которая зависит от его геометрической формы. В таблице ниже представлены основные формулы для вычисления объема различных геометрических фигур.
| Фигура | Формула для вычисления объема |
|---|---|
| Параллелепипед | Объем = Длина x Ширина x Высота |
| Пирамида | Объем = (Площадь основания x Высота) / 3 |
| Цилиндр | Объем = Площадь основания x Высота |
| Шар | Объем = (4/3) x Пи x Радиус^3 |
Если известны площадь основания и высота объекта, то с помощью данных формул вы сможете легко вычислить его объем. Важно помнить, что все значения должны быть выражены в одной системе измерения, например, в сантиметрах или метрах.
Вычисление объема: примеры задач
Чтобы проиллюстрировать, как вычисляется объем при помощи формулы, рассмотрим несколько примеров задач.
Пример 1: Найдите объем параллелепипеда со сторонами a = 5 см, b = 7 см и c = 10 см.
Для нахождения объема параллелепипеда воспользуемся формулой: V = a * b * c. Подставим значения a, b и c в формулу: V = 5 см * 7 см * 10 см = 350 см³.
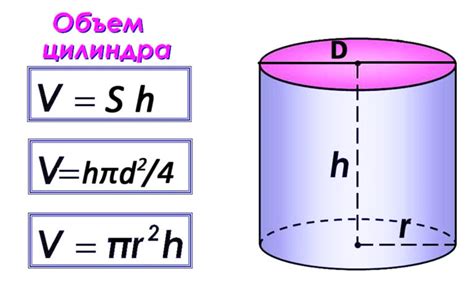
Пример 2: Вычислите объем цилиндра, если его радиус равен 4 см, а высота равна 10 см.
Для вычисления объема цилиндра используем формулу: V = π * r² * h, где π (пи) – это математическая константа, приближенное значение которой равно 3,14. Подставим значения r и h в формулу: V = 3,14 * (4 см)² * 10 см = 502,4 см³.
Пример 3: Найдите объем шара с радиусом 6 см.
Формула для вычисления объема шара: V = (4/3) * π * r³. Подставим значение r в формулу: V = (4/3) * 3,14 * (6 см)³ = 904,32 см³.
Таким образом, использование соответствующих формул позволяет легко вычислить объем тела, если известны его параметры.
Применение формулы объема в повседневной жизни

Формула вычисления объема важна не только в математических расчетах, но и применяется в повседневной жизни. Знание этой формулы может быть полезным при решении реальных задач и позволяет более обоснованно принимать решения.
Одним из примеров применения формулы объема является строительство и ремонт. При покупке стройматериалов, таких как кирпичи, плиты или блоки, знание объема помещения позволяет рассчитать необходимое количество материалов, исходя из его площади и высоты. Таким образом, можно избежать излишнего расходования средств или недостатка материалов.
Еще одним примером является сфера торговли. При дизайне торговых пространств или складов, знание объема помещения помогает оптимизировать расстановку товаров или упаковок. Также, при перевозке товаров, учет объема помещения в грузовом автомобиле или контейнере важен для определения грузоподъемности и типа транспорта, который может быть использован для перевозки.
Кроме того, формула объема может быть применена в сфере сельского хозяйства. Например, для определения объема контейнеров или резервуаров для хранения жидкостей или зерна. Знание объема позволяет определить необходимое количество или запасы продуктов, а также планировать их использование.
Таким образом, формула объема является полезным инструментом в повседневной жизни, который помогает решать разнообразные задачи в различных сферах деятельности. Умение использовать эту формулу позволяет экономить ресурсы, оптимизировать процессы и принимать взвешенные решения на основе объективной информации.