Призма - это геометрическое тело, образованное двумя конгруэнтными (равными по форме и размеру) многоугольниками, называемыми основаниями, и прямоугольниками, называемыми боковыми гранями. Нахождение объема и площади поверхности призмы является важной задачей в геометрии.
Объем призмы может быть определен как произведение площади основания на высоту. Если основание призмы - многоугольник, то площадь можно найти, разбивая его на треугольники или другие фигуры с более простыми формами. Далее, нужно умножить полученную площадь на высоту призмы, что даст объем.
Чтобы найти площадь поверхности призмы, нужно найти сумму площадей всех боковых граней и площадей двух оснований призмы. Если основания являются многоугольниками, может потребоваться разбить их на более простые фигуры и вычислить отдельно площади каждой из них.
Призмы встречаются во многих областях науки и техники, и умение находить их объем и площадь поверхности может быть полезным при решении различных практических задач. В следующих примерах мы рассмотрим как найти объем и площадь поверхности различных типов призм. Эти примеры помогут тебе лучше понять основные принципы расчетов и применение формул, используемых при нахождении данных характеристик призмы.
Как рассчитать объем и площадь поверхности призмы: подробное объяснение и примеры расчетов
Чтобы найти объем призмы, нужно умножить площадь основания на высоту. Найдем площадь поверхности призмы, вычислим площади всех ее боковых граней и сложим их вместе. Расчеты могут быть сложными, поэтому рекомендуется использовать следующую формулу для рассчета площади поверхности призмы:
S = 2 * Sосн + Sбок,
где Sосн - площадь одного основания призмы, а Sбок - сумма площадей боковых граней. Чтобы найти Sбок, нужно умножить периметр основания на высоту призмы.
Приведем примеры расчетов объема и площади поверхности для призмы.
Пример 1:
Дана прямоугольная призма с основанием 5x8 см и высотой 10 см.
1. Вычисляем площадь одного основания: Sосн = 5 см * 8 см = 40 см2.
2. Вычисляем площадь боковых граней: Sбок = (5 см + 8 см) * 10 см = 130 см2.
3. Вычисляем площадь поверхности призмы: S = 2 * 40 см2 + 130 см2 = 210 см2.
4. Вычисляем объем призмы: V = 40 см2 * 10 см = 400 см3.
Пример 2:
Дана правильная треугольная призма с высотой 12 см и стороной основания 6 см.
1. Вычисляем площадь одного основания: Sосн = (√3 * a2) / 4 = (√3 * 6 см * 6 см) / 4 = 9√3 см2.
2. Вычисляем площадь боковых граней: Sбок = (a + b + c) * h = (6 см + 6 см + 8 см) * 12 см = 480 см2.
3. Вычисляем площадь поверхности призмы: S = 2 * 9√3 см2 + 480 см2 = 18√3 + 480 см2.
4. Вычисляем объем призмы: V = 9√3 см2 * 12 см ≈ 324 см3.
Теперь вы знаете, как рассчитать объем и площадь поверхности призмы. Эти формулы помогут вам проводить необходимые расчеты и использовать полученные результаты в практических задачах.
Что такое призма: определение и характеристики
Важнейшей характеристикой призмы является высота, которая определяется как расстояние между плоскостями оснований. Высота призмы всегда перпендикулярна плоскости основания и позволяет определить ее объем и площадь поверхности.
Еще одной важной характеристикой призмы является боковая грань, которая представляет собой многоугольник, состоящий из отрезков, соединяющих соответствующие вершины оснований. Боковая грань является прямоугольником, если основания призмы являются прямоугольниками, и прым слоен, если основания являются многоугольниками любой другой формы.
Кроме того, призма имеет два основания, которые являются параллельными плоскостями, ограничивающими тело снизу и сверху. Основания могут быть разных форм и размеров, что влияет на форму и размеры призмы.
Изучение характеристик призмы позволяет лучше понять ее геометрию и использовать руководство для расчета объема и площади поверхности. Это особенно полезно при решении задач в физике, инженерии и архитектуре, где призмы являются важными элементами конструкций и объектов.
Формулы для расчета объема и площади поверхности призмы
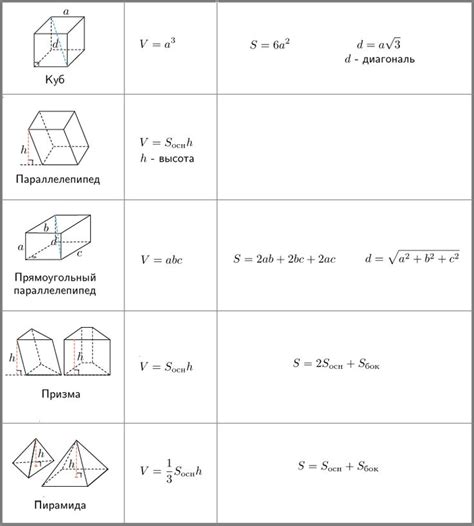
Расчет объема и площади поверхности призмы осуществляется с помощью определенных формул, которые зависят от вида призмы.
Для правильной прямоугольной призмы формула для расчета объема имеет вид:
V = a * b * h
где a - длина основания призмы, b - ширина основания призмы, h - высота призмы.
Формула для расчета площади поверхности правильной прямоугольной призмы:
S = 2 * (a * b + a * h + b * h)
Для правильной треугольной призмы формула для расчета объема имеет вид:
V = (1/4) * a^2 * h * √3
где a - длина стороны основания призмы, h - высота призмы.
Формула для расчета площади поверхности правильной треугольной призмы:
S = a * (a + √3 * h)
Зная значения длины, ширины и высоты призмы, можно применить соответствующие формулы для рассчета объема и площади поверхности призмы.
Как найти объем призмы: шаги и примеры расчетов

Для расчета объема призмы необходимо знать площадь основания и высоту призмы.
- Определите площадь основания. Для этого необходимо знать форму основания призмы. Расчет площади основания может отличаться в зависимости от формы (квадрат, прямоугольник, треугольник и т.д.).
- Измерьте высоту призмы. Высота - это расстояние между основаниями призмы.
- Умножьте площадь основания на высоту призмы. Формула для расчета объема призмы: V = S * h, где V - объем, S - площадь основания и h - высота призмы.
Давайте рассмотрим пример расчета объема призмы с квадратным основанием и высотой 5 см.
| Основание (S) | Высота (h) | Объем (V) |
|---|---|---|
| 9 см² | 5 см | 45 см³ |
Итак, объем призмы с квадратным основанием площадью 9 см² и высотой 5 см равен 45 см³.
Теперь вы знаете, как найти объем призмы и можете использовать данную информацию при решении задач по геометрии и приложениях в повседневной жизни.
Как найти площадь поверхности призмы: пошаговое руководство и примеры

- Определите тип призмы: Призма может быть прямоугольной или треугольной. Исходя из типа призмы, вы определите форму ее основания.
- Найдите площади оснований: Для прямоугольной призмы, умножьте длину основания на ширину основания. Для треугольной призмы, найдите площадь треугольника с помощью соответствующей формулы.
- Найдите площади боковых граней: Для прямоугольной призмы, умножьте периметр основания на высоту призмы. Для треугольной призмы, умножьте половину периметра основания на высоту призмы.
- Просуммируйте все площади: Сложите площади оснований и боковых граней, чтобы найти общую площадь поверхности призмы.
Вот пример расчета площади поверхности призмы:
Пусть у нас есть прямоугольная призма с длиной основания 5 см, шириной основания 3 см и высотой призмы 8 см.
- Площадь основания: 5 см * 3 см = 15 см²
- Площадь боковых граней: (5 см + 3 см) * 8 см = 64 см²
Суммируем площади оснований и боковых граней: 15 см² + 64 см² = 79 см²
Таким образом, площадь поверхности этой прямоугольной призмы равна 79 см².
Будьте внимательны при вычислении и убедитесь, что вы правильно определили формы оснований и правильно применили формулы для нахождения площадей. Следуя описанному выше пошаговому руководству, вы сможете легко найти площадь поверхности любой призмы.
Применение расчетов объема и площади поверхности призмы в реальной жизни
Расчеты объема и площади поверхности призмы на первый взгляд могут показаться абстрактными математическими задачами. Однако, эти расчеты имеют широкое практическое применение и находят свое применение в различных сферах нашей жизни.
В строительстве, расчеты объема и площади поверхности призмы необходимы для определения количества строительных материалов, таких как бетон, кирпичи или стекло, необходимых для возведения призматических форм зданий или конструкций. Например, при строительстве бассейна или аквариума, зная объем призмы, можно определить количество воды, необходимое для заполнения, а также количество фильтров и химических препаратов для обработки воды.
В производстве, расчеты объема и площади поверхности призмы используются для определения объема сырья, необходимого для производства продукта или детали. Например, при производстве стеклянных бутылок, зная объем призмы, можно определить, сколько стекла понадобится для изготовления определенного количества бутылок.
В геометрическом моделировании и дизайне, знание объема и площади поверхности призмы является необходимым для создания трехмерных моделей, архитектурных проектов или разработки уникальных деталей. Расчеты позволяют определить пропорции и объемы объектов, что помогает в создании эстетически привлекательных и функциональных продуктов.
Использование расчетов объема и площади поверхности призмы не ограничено только вышеперечисленными областями. Они также находят свое применение в науке, физике, медицине, технике и многих других сферах деятельности человека.