Куб – это геометрическое тело с шестью равными гранями. Каждая его грань – квадрат, а все его углы прямые. Как найти объем куба? Существует несколько способов решения этой задачи. Рассмотрим один из самых популярных – расчет по диагонали основания.
Диагональ основания куба – это отрезок, соединяющий противоположные вершины основания. Она проходит по его диагонали. Для решения задачи необходимо знать длину диагонали основания, а также понимать, что объем куба выражается формулой V = a³, где a – длина ребра куба. Теперь найдем значение a.
Поскольку диагональ основания – это гипотенуза прямоугольного треугольника, образованная двумя ребрами куба, то можно воспользоваться теоремой Пифагора для расчета длины ребра a. А именно: a = √(d²/2), где d – длина диагонали основания. Теперь, зная длину ребра, мы можем использовать формулу V = a³ для определения объема куба.
Как найти объем куба?

Формула для расчета объема куба: V = a^3, где "V" - объем, "a" - длина стороны.
Чтобы найти объем куба, нужно возведенить в куб длину его стороны.
Пример:
Пусть длина стороны куба равна 5 см.
Используя формулу, найдем его объем: V = 5^3 = 125 см^3.
Таким образом, объем куба с длиной стороны 5 см равен 125 кубическим сантиметрам.
Формула расчета объема куба
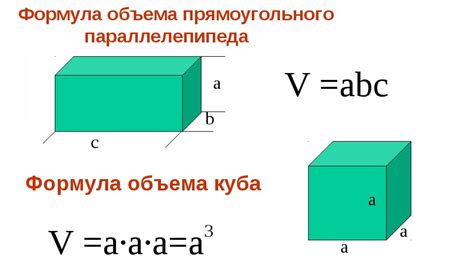
Для того чтобы найти объем куба по диагонали основания, сначала необходимо найти длину ребра. Диагональ основания куба составляет g = a√2, где g - диагональ основания, a - длина ребра.
Таким образом, формула для расчета объема куба по диагонали основания будет выглядеть следующим образом: V = (g/√2)^3.
Пример расчета объема куба по диагонали основания:
Пусть диагональ основания куба равна 10 см. Найдем длину ребра:
a = g/√2 = 10/√2 ≈ 7.07 см.
Теперь можем рассчитать объем куба:
V = a^3 = (7.07)^3 ≈ 353.44 см^3.
Таким образом, объем куба с диагональю основания 10 см составляет примерно 353.44 см^3.
Расчет объема куба по диагонали основания
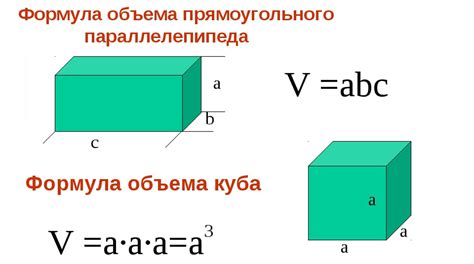
Если известна длина диагонали основания, можно использовать формулу для расчета объема куба:
Объем куба = (Диагональ^3) / (3 * √2)
Где:
- Диагональ - длина диагонали основания.
Давайте рассмотрим пример расчета объема куба по диагонали основания:
Пусть длина диагонали основания куба равна 10 см. Тогда, подставляя значение в формулу, получаем:
Объем куба = (10^3) / (3 * √2) = 1000 / (3 * 1.414) ≈ 235.702 см³
Таким образом, объем куба со сторонами, диагональ основания которых равна 10 см, составляет около 235.702 см³.
Используя данную формулу и зная длину диагонали основания куба, вы сможете легко и быстро рассчитать его объем.
Примеры расчета объема куба
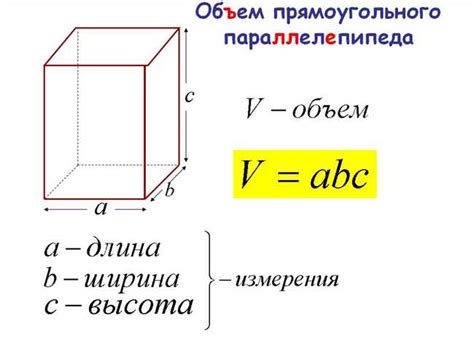
Приведем несколько примеров, как найти объем куба, используя формулу, основанную на длине диагонали основания.
| Пример | Диагональ основания (d) | Объем куба (V) |
|---|---|---|
| Пример 1 | 4 см | 64 см³ |
| Пример 2 | 8 см | 512 см³ |
| Пример 3 | 10 см | 1000 см³ |
Как видно из примеров, чтобы найти объем куба по диагонали основания, нужно возвести длину диагонали в куб и полученное значение будет являться объемом куба.