Многогранник - это геометрическая фигура, имеющая плоские грани и углы между ними. В школьной программе 6 класса ученикам предлагается изучить основные понятия связанные с многогранниками, а именно: вершину, грань, ребро.
Объем многогранника - это величина, которая показывает, сколько пространства занимает эта фигура. Расчет объема многогранника позволяет узнать его размеры и использовать полученные значения для решения различных задач.
Существует несколько формул для нахождения объема многогранника в зависимости от его типа. Например, для параллелепипеда можно использовать формулу: V = a * b * c, где a, b, c - длины трех сторон параллелепипеда.
Если речь идет о пирамиде, то формула упрощается и имеет вид: V = (S основания * h) / 3, где S - площадь основания, h - высота пирамиды.
Важно понимать, что для успешного решения задач по нахождению объема многогранников необходимо хорошо знать основные понятия и формулы для каждого типа многогранника. Знание этих навыков поможет ученикам успешно справляться с заданиями на уроках и контрольных работах.
Как узнать объем многогранника: формула и примеры для учеников 6 класса
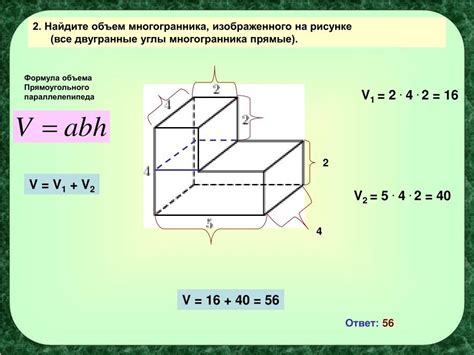
Формула для нахождения объема многогранника зависит от его типа. Например, для прямоугольного параллелепипеда объем вычисляется по формуле:
V = a * b * h
где a, b и h - длины трех взаимно перпендикулярных ребер многогранника.
Давайте рассмотрим пример нахождения объема параллелепипеда. Предположим, что у нас есть прямоугольный параллелепипед, у которого стороны a = 4 см, b = 3 см и h = 5 см. Подставив значения в формулу, получим:
| Длина (см) | Ширина (см) | Высота (см) | Объем (см³) |
|---|---|---|---|
| 4 | 3 | 5 | 60 |
Таким образом, объем данного параллелепипеда равен 60 кубическим сантиметрам.
Для других типов многогранников существуют свои формулы для вычисления объема. Например, для куба все ребра имеют одинаковую длину, поэтому формула сводится к возведению длины ребра в куб:
V = a³
Что такое многогранник?

Многогранники классифицируются в зависимости от количества граней и их формы. Например, треугольная пирамида, куб, призма, октаэдр - это различные типы многогранников.
Чтобы найти объем многогранника, необходимо знать его формулу объема, которая зависит от типа многогранника. Например, для куба формула объема будет V = a^3, где a - длина ребра.
Изучение многогранников позволяет развивать пространственное мышление, так как они имеют трехмерную форму. Это помогает решать задачи в геометрии и находить объемы различных объектов, таких как ящики, аквариумы и другие предметы в повседневной жизни.
Как определить тип многогранника?

Существует несколько способов определения типа многогранника:
- Количество граней: если многогранник имеет три грани, он называется трехгранником (пирамидой), четыре грани – четырехгранником (призмой), пять граней – пятигранником (пирамидой), шесть граней – шестигранником (кубом), и так далее.
- Количество вершин: если многогранник имеет четыре вершины, он называется тетраэдром, пять вершин – пирамидой, шесть вершин – призмой, восемь вершин – кубом, и так далее.
- Симметрия: многогранники также могут быть симметричными или несимметричными. Симметричные многогранники могут иметь равные грани, углы и ребра.
Определение типа многогранника может помочь понять его свойства и характеристики. Также, зная тип многогранника, можно легче решать задачи, связанные с его объемом, площадью поверхности и другими параметрами.
Какие фигуры могут быть многогранниками?

Существует множество различных многогранников, каждый из которых имеет свои уникальные свойства и формулы для вычисления их параметров. Некоторые из наиболее известных многогранников:
- Пирамида - многогранник, который имеет одну плоскую основу и треугольные или четырехугольные боковые грани, соединяющиеся с вершиной.
- Призма - многогранник, у которого две плоские фигуры, называемые основаниями, соединяются прямыми линиями, называемыми боковыми гранями.
- Куб - многогранник, все грани которого имеют одинаковую форму и размер, а вершины соединяются ребрами под прямым углом.
- Параллелепипед - многогранник, у которого шесть прямоугольных граней, противоположные грани параллельны.
Это лишь некоторые примеры многогранников, так как их разнообразие велико. Каждый многогранник имеет свои особенности и структуру, которая может быть определена с помощью формул и геометрических законов.
Как найти объем основных типов многогранников?

Многогранником называется трехмерная фигура, у которой все грани представляют собой многоугольники. Объем многогранника показывает, сколько пространства он занимает. Зная формулы для вычисления объема различных типов многогранников, можно легко решить задачи на их вычисление.
1. Объем прямоугольного параллелепипеда вычисляется по формуле V = a * b * h, где a, b и h – длины трех ребер, сходящихся в одной вершине. Эту формулу можно применять для вычисления объема куба, прямоугольного параллелепипеда и призмы.
2. Объем пирамиды вычисляется по формуле V = (1/3) * S * h, где S – площадь основания пирамиды, а h – высота пирамиды. При вычислении объема пирамиды нужно знать ее площадь основания и высоту.
3. Объем цилиндра вычисляется по формуле V = π * r^2 * h, где r – радиус основания цилиндра, а h – высота цилиндра. В этой формуле π равно приблизительно 3,14. Для вычисления объема цилиндра необходимо знать радиус его основания и высоту.
4. Объем конуса вычисляется по формуле V = (1/3) * π * r^2 * h, где r – радиус основания конуса, а h – высота конуса. Также как и для цилиндра, в этой формуле π равно примерно 3,14. При вычислении объема конуса нужно знать его радиус и высоту.
Зная эти формулы, вы можете легко вычислить объем различных многогранников и применить их при решении задач.
Примеры решения задач по нахождению объема многогранников
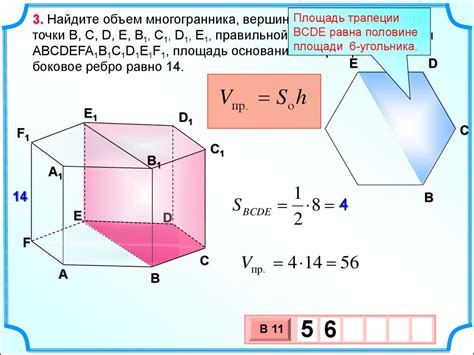
Для нахождения объема многогранника необходимо знать его формулу и измерения его граней. Рассмотрим несколько примеров решения задач по нахождению объемов различных многогранников.
Пример 1: Найдем объем параллелепипеда, у которого длина a = 6 см, ширина b = 4 см и высота c = 3 см. Формула для нахождения объема параллелепипеда: V = a * b * c. Подставляя известные значения, получаем V = 6 * 4 * 3 = 72 см³. Таким образом, объем параллелепипеда равен 72 кубическим сантиметрам.
Пример 2: Найдем объем пирамиды, у которой площадь основания S = 64 см², а высота h = 8 см. Формула для нахождения объема пирамиды: V = (1/3) * S * h. Подставляя известные значения, получаем V = (1/3) * 64 * 8 = 170,67 см³ (округляем до двух знаков после запятой). Таким образом, объем пирамиды примерно равен 170,67 кубическим сантиметрам.
Пример 3: Найдем объем шара, у которого радиус r = 5 см. Формула для нахождения объема шара: V = (4/3) * π * r³. Подставляя известные значения и принимая π приближенно равным 3,14, получаем V = (4/3) * 3,14 * 5³ = 523,33 см³ (округляем до двух знаков после запятой). Таким образом, объем шара примерно равен 523,33 кубическим сантиметрам.
Таким образом, для решения задач по нахождению объемов многогранников необходимо знать формулу для каждого конкретного многогранника и подставить известные значения в эту формулу. Полученное значение будет являться объемом многогранника и измеряется в кубических единицах, например, в кубических сантиметрах.
Рекомендации для учеников 6 класса по изучению темы

1. Внимательно прочитайте учебник или материалы, предоставленные учителем. Изучите определения ключевых понятий, таких как многогранник, грань, вершина и подобные. Попросите учителя объяснить непонятные моменты.
2. Подготовьте таблицу с формулами для нахождения объема разных видов многогранников. В таблице укажите название многогранника, его формулу для расчета объема и примеры задач для отработки навыка применения формулы.
| Название многогранника | Формула для расчета объема | Пример задачи |
|---|---|---|
| Параллелепипед | Объем = длина * ширина * высота | Найдите объем параллелепипеда со сторонами 3 см, 4 см и 5 см. |
| Пирамида | Объем = (площадь основания * высота) / 3 | Найдите объем пирамиды с основанием в виде прямоугольного треугольника с катетами 6 см и 8 см, а высотой 10 см. |
| Шар | Объем = (4 / 3) * π * радиус^3 | Найдите объем шара с радиусом 5 см. |
3. Решайте задачи, связанные с нахождением объема многогранников, как в учебнике, так и в дополнительных учебных материалах. Постепенно увеличивайте сложность задач, чтобы закрепить свои навыки и развить логическое мышление.
4. Используйте геометрические модели, если это возможно. Нарисуйте многогранники на бумаге или создайте их из конструктора. Это поможет вам лучше понять структуру многогранников и визуализировать процесс нахождения их объема.
5. Постоянно повторяйте материал и решайте похожие задачи. Практика способствует закреплению знаний и развитию навыков решения задач по нахождению объема многогранников.
Следуя этим рекомендациям, вы сможете успешно освоить тему по нахождению объема многогранника и добиться хороших результатов на уроках математики!