Окружность – это геометрическая фигура, которая может вызывать много вопросов у тех, кто только знакомится с математикой. Ее длина, площадь и радиус являются важными характеристиками этой фигуры. Но что насчет объема окружности? На первый взгляд может показаться, что окружность – это плоская фигура и ее объем невозможно посчитать. Однако, существует способ определить объем окружности, если известен его диаметр.
Первым шагом для определения объема окружности по диаметру является нахождение ее радиуса. Радиус – это расстояние от центра окружности до любой точки на окружности. Он является половиной диаметра. Поэтому, чтобы найти радиус, необходимо разделить диаметр на 2. Например, если диаметр равен 10 см, то радиус будет 5 см.
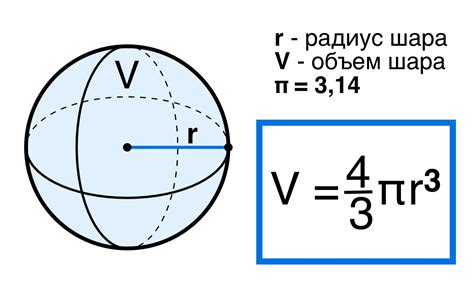
После нахождения радиуса, можно перейти к определению объема окружности. Объем – это объем пространства, занимаемого объектом. В случае окружности объем можно найти с помощью формулы объема шара, так как шар является трехмерным представлением окружности. Формула объема шара выглядит следующим образом: V = (4/3)πr³, где V – объем, π – число Пи (приближенное значение 3,14), r – радиус. Подставив значение радиуса, мы получим искомый объем окружности.
Формула для вычисления объема окружности
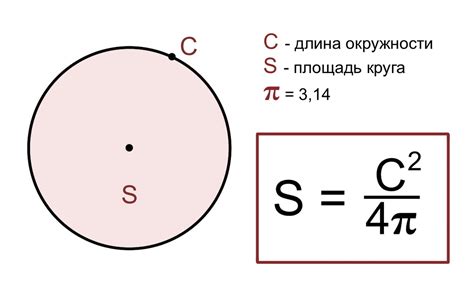
Для вычисления объема окружности необходимо знать ее диаметр или радиус.
Окружность - это плоская фигура, каждая точка на которой находится на одинаковом расстоянии от центра. Объем окружности является трехмерной величиной и вычисляется с использованием формулы.
Формула для вычисления объема окружности:
- Первоначально необходимо найти площадь окружности по формуле S = π * r^2, где π (пи) - математическая константа, равная примерно 3,14159, а r - радиус окружности.
- Далее, объем окружности можно вычислить по формуле V = S * h, где V - объем, S - площадь окружности и h - высота окружности.
Используя данные формулы, можно получить точное значение объема окружности по ее диаметру или радиусу. Эта формула широко используется в математике, физике, инженерии и других научных областях.
Что такое диаметр и как его измерить

Для измерения диаметра окружности можно воспользоваться различными инструментами, такими как:
- линейка – для измерения небольших диаметров;
- штангенциркуль – для точного измерения диаметра;
- микрометр – для измерения диаметров с высокой точностью.
При измерении диаметра необходимо учитывать, что он должен проходить через центр окружности, а также быть перпендикулярен к ее касательной.
Знание диаметра окружности позволяет решать различные задачи, связанные с геометрией, инженерией, а также находить его объем и площадь.
Пример вычисления объема окружности для конкретного диаметра
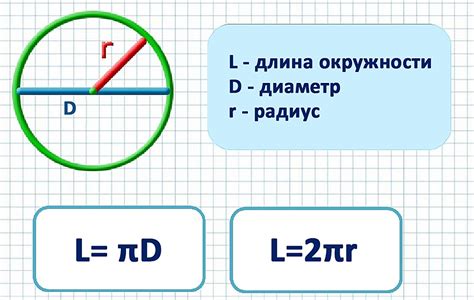
Для вычисления объема окружности по заданному диаметру необходимо использовать следующую формулу:
- Найти радиус окружности, поделив диаметр на два.
- Возвести радиус в квадрат.
- Умножить полученное значение на число пи (π), которое примерно равно 3.14159.
Для наглядности рассмотрим пример. Пусть дан диаметр окружности, равный 10 единиц.
- Радиус будет равен 10 / 2 = 5 единиц.
- Возведем радиус в квадрат: 5 * 5 = 25.
- Умножим полученное значение на число пи: 25 * 3.14159 = 78.53975.
Таким образом, объем окружности с диаметром 10 будет равен примерно 78.53975 единиц.
Как использовать физические константы при вычислении объема окружности
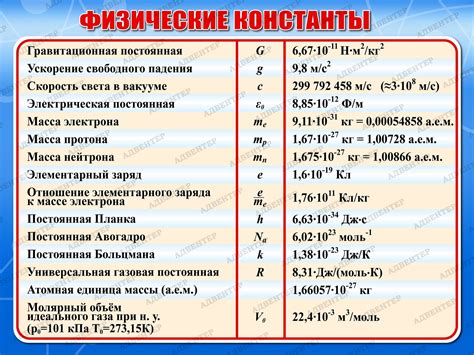
При вычислении объема окружности можно использовать не только математические формулы, но и физические константы. Физические константы представляют собой значения, которые не изменяются и имеют всеобщее значение в науке и инженерии.
Одной из физических констант, которую можно использовать при вычислении объема окружности, является число Пи (π). Число Пи равно отношению длины окружности к ее диаметру и приближенно равно 3,14159.
Формула для вычисления объема окружности с использованием физической константы числа Пи выглядит следующим образом:
V = (4/3) * π * (r^3),
где V - объем окружности, π - число Пи (примерно равно 3,14159), r - радиус окружности.
Пример вычисления объема окружности:
r = 5 см
V = (4/3) * 3,14159 * (5^3)
V ≈ 523,599 см³ Таким образом, использование физической константы числа Пи позволяет точно и удобно вычислять объем окружности
Математические основы для вычисления объема окружности
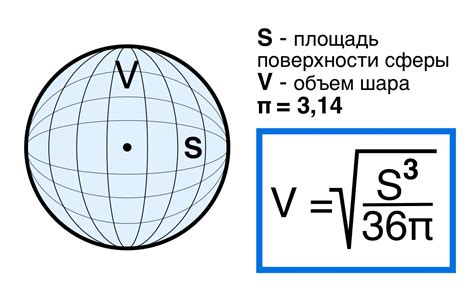
Для вычисления объема окружности нам понадобится знать ее радиус или диаметр. Радиус окружности - это расстояние от центра окружности до любой точки на ее окружности, а диаметр - это расстояние между двумя точками на окружности, через центр.
Формула для вычисления объема окружности по диаметру выглядит следующим образом:
V = (4/3) * π * (d/2)^3
где V - объем окружности, d - диаметр окружности, π - математическая константа, приближенно равная 3.14159.
Данная формула основана на том факте, что объем сферы, образующейся поворотом окружности вокруг ее диаметра, равен этой формуле. Таким образом, вычисление объема окружности сводится к вычислению объема сферы, с которой она тесно связана.
Для использования формулы необходимо знать значение диаметра окружности. Если известен только радиус, его можно вычислить, умножив значение радиуса на 2.
Например, для окружности с диаметром 10 см, объем можно вычислить следующим образом:
V = (4/3) * π * (10/2)^3
где π приблизительно равно 3.14159.
Таким образом, вычисляем объем:
V = (4/3) * 3.14159 * 5^3 ≈ 523.6 см³
Полученный результат - объем окружности с диаметром 10 см. Точно также можно вычислить объем окружности с помощью ее радиуса:
V = (4/3) * 3.14159 * (10/2)^3 ≈ 523.6 см³
Зная математические основы для вычисления объема окружности, вы сможете применить данную формулу для других значений диаметра и получить объем окружности в соответствии с задачей.
Как выразить диаметр, редуцированный диаметр и диаметральное сечение при вычислении объема окружности

Следующим важным понятием является редуцированный диаметр. Редуцированный диаметр обозначается символом "dr". Он равен диаметру окружности, уменьшенной на толщину стенки, если она присутствует. Редуцированный диаметр обычно используется при расчете объема цилиндра с отверстием.
Диаметральное сечение - это сечение окружности, которое перпендикулярно диаметру и проходит через его середину. При вычислении объема окружности с помощью диаметрального сечения необходимо знать его диаметр. Объем, вычисленный с использованием диаметрального сечения, будет равен объему, вычисленному с использованием диаметра.
Использование правильных понятий и выражений, таких как диаметр, редуцированный диаметр и диаметральное сечение, позволяет точно вычислить объем окружности и получить правильные результаты.
Практическое применение формулы для вычисления объема окружности
Вычисление объема окружности может быть полезным во множестве ситуаций. Одним из примеров использования этой формулы может быть нахождение объема цилиндра, основой которого является окружность.
Например, если вы работаете в строительной или инженерной сфере, вам может понадобиться вычислить объем резервуара или бочки, которые имеют форму цилиндра. С помощью формулы для вычисления объема окружности можно легко найти нужное значение и использовать его для расчетов.
Также формула для вычисления объема окружности может быть полезной при изучении физики или математики. Она поможет вам решать задачи, связанные с геометрическими фигурами и их объемами.
Давайте рассмотрим пример. Предположим, у вас есть резервуар диаметром 4 метра и вы хотите вычислить его объем. Используя формулу для вычисления объема окружности, можно сделать следующий расчет:
| Параметр | Значение |
|---|---|
| Диаметр окружности | 4 метра |
| Радиус окружности | 2 метра (половина диаметра) |
| Площадь окружности | 12.57 метра квадратного (по формуле S = π * r^2) |
| Объем резервуара | 37.7 метра кубического (по формуле V = S * h, где h - высота резервуара) |
Таким образом, при диаметре резервуара 4 метра его объем составит примерно 37.7 метра кубического.
Использование формулы для вычисления объема окружности позволяет решать практические задачи эффективно и точно. Зная диаметр окружности, вы можете вычислить ее объем и применить эту информацию в различных областях своей деятельности.