Параллелепипед - это геометрическое тело, у которого все грани являются прямоугольниками. В школьной программе в 5 классе вводится понятие объема параллелепипеда и способы его нахождения. Если ты хочешь научиться находить объем этой фигуры, то эта статья для тебя!
Формула для нахождения объема параллелепипеда очень простая. Для этого нужно умножить длину на ширину на высоту. То есть, если длина параллелепипеда равна а, ширина равна b, а высота равна с, то его объем можно выразить по формуле: V = a * b * c.
Давай посмотрим на пример. Представь, что у тебя есть параллелепипед со сторонами 4 см, 3 см и 5 см. Чтобы найти его объем, нужно умножить эти три числа: 4 * 3 * 5 = 60 см³. Это и есть объем данного параллелепипеда, который равен 60 кубическим сантиметрам.
Как найти объем параллелепипеда: основная формула и принципы расчета
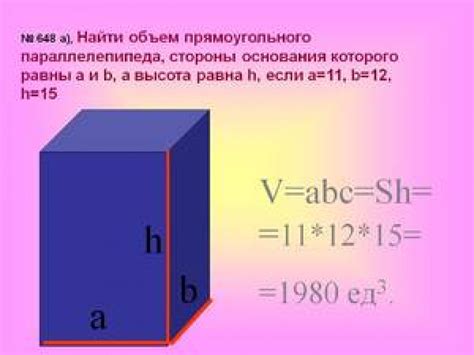
Основная формула для вычисления объема параллелепипеда выглядит следующим образом:
V = a * b * c,
где V - объем параллелепипеда, a - длина одной из его сторон, b - длина второй стороны и c - длина третьей стороны.
Чтобы вычислить объем параллелепипеда, необходимо знать длины всех его сторон. Эти значения могут быть даны в различных единицах измерения, таких как сантиметры, метры или дюймы. Важно убедиться, что все величины используются в одной и той же системе измерения.
Пример:
Предположим, что у нас есть параллелепипед, у которого одна сторона равна 5 см, вторая - 8 см и третья - 10 см. Используя основную формулу, мы можем вычислить его объем:
V = 5 см * 8 см * 10 см = 400 см³.
Таким образом, объем этого параллелепипеда составляет 400 кубических сантиметров.
Знание основной формулы и принципов расчета объема параллелепипеда позволяет эффективно решать задачи, связанные с этой фигурой, и применять их в реальной жизни.
Принципы расчета объема параллелепипеда
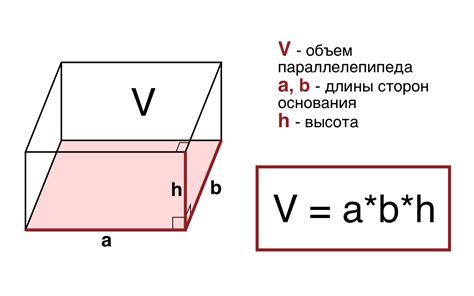
Объем параллелепипеда можно выразить формулой: объем = длина × ширина × высота.
Приведем пример расчета объема параллелепипеда:
Пусть у нас есть параллелепипед с длиной 4 см, шириной 5 см и высотой 3 см. Чтобы найти его объем, нужно перемножить эти значения: 4 × 5 × 3 = 60 см³.
Таким образом, объем этого параллелепипеда равен 60 см³.
Изучение принципов расчета объема параллелепипеда позволяет нам понять, как измерять и сравнивать объемы различных фигур, а также использовать этот навык в решении задач по геометрии и пространственной математике.
Основная формула для определения объема параллелепипеда
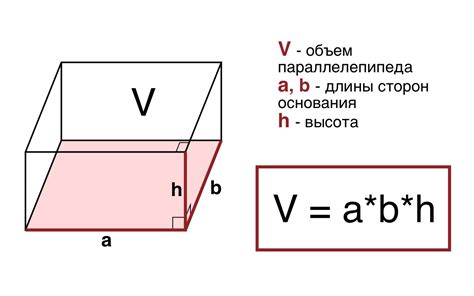
Объем параллелепипеда можно вычислить, используя основную формулу. Формула для определения объема параллелепипеда такая:
Объем = длина × ширина × высота.
Для того чтобы найти объем параллелепипеда, нужно знать все три измерения: длину, ширину и высоту. Длина, ширина и высота должны быть выражены в одной и той же единице измерения. Например, если длина параллелепипеда равна 10 сантиметрам, ширина - 5 сантиметрам, а высота - 3 сантиметра, то объем можно вычислить так: 10 см × 5 см × 3 см = 150 см³.
Таким образом, основная формула для определения объема параллелепипеда позволяет найти объем тела, зная его геометрические размеры.
Примеры нахождения объема параллелепипеда для 5 класса
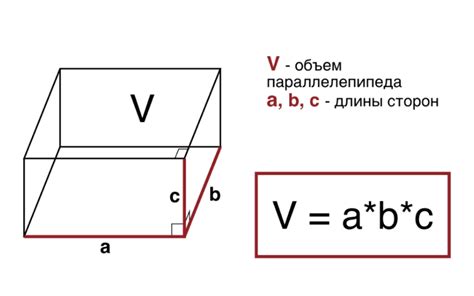
Рассмотрим пример. Пусть длина параллелепипеда равна 4 см, ширина равна 3 см, а высота равна 5 см:
Решение:
Используем формулу V = a * b * h.
V = 4 см * 3 см * 5 см.
V = 60 см³.
Ответ: объем параллелепипеда равен 60 см³.
Другой пример. Пусть дан параллелепипед со сторонами a = 6 см, b = 8 см и h = 10 см:
Решение:
Используем формулу V = a * b * h.
V = 6 см * 8 см * 10 см.
V = 480 см³.
Ответ: объем параллелепипеда равен 480 см³.
Пример 1: Расчет объема параллелепипеда с заданными сторонами
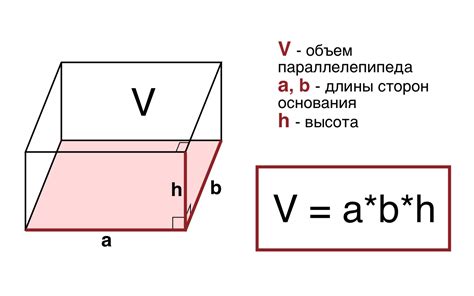
Чтобы найти объем такого параллелепипеда, необходимо воспользоваться формулой: объем = длина * ширина * высота. В нашем случае, это будет выглядеть так:
| Длина (см) | Ширина (см) | Высота (см) | Объем (см³) |
|---|---|---|---|
| 10 | 5 | 3 | 150 |
Таким образом, объем этого параллелепипеда составляет 150 кубических сантиметров.
Пример 2: Определение неизвестного измерения по известным данным объема и известным сторонам параллелепипеда

Решение этой задачи основано на формуле для вычисления объема параллелепипеда:
V = a * b * c,
где V - объем параллелепипеда, a, b и c - длины трех его сторон.
Допустим, что мы знаем значения сторон a и b, а также объем V. Чтобы найти значение третьей стороны c, мы можем преобразовать исходную формулу следующим образом:
c = V / (a * b).
То есть, значение третьей стороны равно отношению объема к произведению значений известных сторон a и b.
Давайте рассмотрим пример:
| Известные данные: | Значение: |
|---|---|
| Длина стороны a: | 4 см |
| Длина стороны b: | 3 см |
| Объем параллелепипеда V: | 24 см³ |
Используя формулу, мы можем найти значение третьей стороны c:
c = 24 см³ / (4 см * 3 см) = 2 см.
Таким образом, длина третьей стороны параллелепипеда равна 2 см.
Используя этот метод, можно находить неизвестные измерения трехмерных фигур, зная их объем и значения известных сторон.