Параллелепипед – это геометрическая фигура с шестью гранями, у которой все грани являются прямоугольниками. Каждый угол параллелепипеда – прямой угол. Объем параллелепипеда определяет, сколько пространства занимает эта фигура. Знание как найти объем параллелепипеда полезно не только для школы, но и в повседневной жизни.
Для вычисления объема параллелепипеда необходимо знать длину, ширину и высоту фигуры. Обозначим их как а, b и с соответственно. Формула для нахождения объема параллелепипеда проста: V = а * b * с. Разумеется, все значения должны быть выражены в одной единице длины – например, в сантиметрах или метрах.
Применение формулы для нахождения объема параллелепипеда позволяет быстро и точно решить задачу, а также научиться применять математические знания на практике. Помимо обычного параллелепипеда, существуют также другие виды параллелепипедов, например, прямоугольные параллелепипеды, кубы и т.д.
Постановка задачи

Задача состоит в нахождении объема параллелепипеда, используя известные значения его длины, ширины и высоты.
Параллелепипед – это геометрическое тело, у которого все грани являются параллелограммами. У него есть три измерения: длина, ширина и высота.
Чтобы найти объем параллелепипеда, нужно знать значения длины, ширины и высоты и применить соответствующую формулу.
Для нахождения объема параллелепипеда используется формула:
| Формула: | Объем параллелепипеда = длина × ширина × высота |
| Обозначения: | Длина - a |
| Ширина - b | |
| Высота - h |
Научимся находить объем параллелепипеда, используя данную формулу в примерах и упражнениях.
Определение понятия параллелепипед
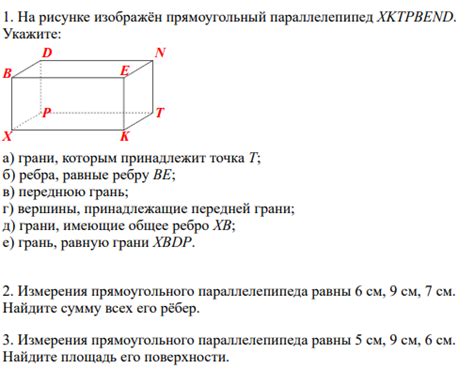
- У него есть шесть граней, причем каждый угол параллелепипеда является прямым.
- Противоположные грани параллелепипеда параллельны и равны друг другу.
- У каждой грани есть свое название: основаниями параллелепипеда являются две пары параллельных граней, а боковыми гранями – остальные четыре грани.
- Векторы, соединяющие противоположные вершины параллелепипеда, имеют равные длины и параллельны друг другу.
Примером параллелепипеда может служить коробка от обуви или книги, так как они обладают всеми указанными выше свойствами.
Формула для вычисления объема параллелепипеда
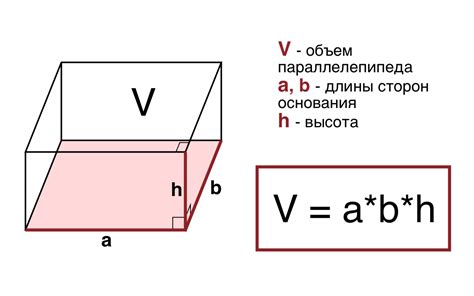
Объем параллелепипеда можно вычислить с помощью следующей формулы:
| объем (V) | = | длина (a) | × | ширина (b) | × | высота (h) |
Эта формула основана на том факте, что объем параллелепипеда можно рассматривать как произведение его трех измерений: длины, ширины и высоты.
Для вычисления объема параллелепипеда нужно знать значения его трех измерений - длины (a), ширины (b) и высоты (h). Умножив эти значения между собой, можно получить объем параллелепипеда.
Например, если длина параллелепипеда равна 5 см, ширина - 3 см, а высота - 4 см, то его объем можно вычислить, умножив эти значения:
| объем (V) | = | 5 см | × | 3 см | × | 4 см | = | 60 см³ |
Таким образом, объем параллелепипеда равен 60 кубическим сантиметрам.
Примеры решения задач:

Пример 1:
- Даны стороны параллелепипеда: a = 3 см, b = 4 см, c = 5 см.
- Чтобы найти объем параллелепипеда, нужно умножить длину, ширину и высоту.
- Объем параллелепипеда равен: V = a * b * c = 3 см * 4 см * 5 см = 60 см³.
Ответ: объем параллелепипеда равен 60 см³.
Пример 2:
- Даны стороны параллелепипеда: a = 6 мм, b = 8 мм, c = 10 мм.
- Чтобы найти объем параллелепипеда, нужно умножить длину, ширину и высоту.
- Объем параллелепипеда равен: V = a * b * c = 6 мм * 8 мм * 10 мм = 480 мм³.
Ответ: объем параллелепипеда равен 480 мм³.
Пример 3:
- Даны стороны параллелепипеда: a = 12 см, b = 15 см, c = 20 см.
- Чтобы найти объем параллелепипеда, нужно умножить длину, ширину и высоту.
- Объем параллелепипеда равен: V = a * b * c = 12 см * 15 см * 20 см = 3600 см³.
Ответ: объем параллелепипеда равен 3600 см³.
Упражнения и практические задания

Для закрепления и углубления понимания объема параллелепипеда, предлагаем вам решить следующие упражнения и практические задания:
- Найдите объем параллелепипеда, если его длина равна 4 см, ширина 3 см и высота 2 см.
- У Васи есть коробка в форме параллелепипеда с длиной 10 см, шириной 5 см и высотой 6 см. Найдите объем этой коробки.
- Изготовьте свою модель параллелепипеда из бумаги или другого материала и определите ее объем. Для этого измерьте длину, ширину и высоту модели в сантиметрах, а затем используйте формулу для нахождения объема параллелепипеда.
- Решите задачу: В гараже имеется коробка в виде параллелепипеда с длиной 5 м, шириной 3 м и высотой 2 м. Какой объем максимально возможного материала можно в нее положить?
- Проверьте свои знания, решив следующую задачу: У Андрея есть аквариум в форме параллелепипеда с длиной 30 см, шириной 20 см и высотой 15 см. Найдите объем в литрах, если 1 литр равен 1000 кубическим сантиметрам.
Решите данные задания самостоятельно, чтобы улучшить понимание темы и навыки нахождения объема параллелепипеда. Если возникнут сложности, не стесняйтесь обратиться за помощью к учителю или одноклассникам.
Объем параллелепипеда выражается в кубических единицах. Например, если размеры параллелепипеда равны 4 см, 5 см и 6 см, то его объем будет равен 4 см × 5 см × 6 см = 120 см³.
Вычисление объема параллелепипеда является важной задачей, так как это позволяет определить, сколько места займет объект или субстанция. Умение находить объем параллелепипеда позволяет решать множество практических задач, связанных с геометрией и ежедневной жизнью.
Зная формулу для вычисления объема параллелепипеда и владея навыками умножения, ты сможешь легко и точно определить объем любого параллелепипеда. Пользуйся этим знанием в своих заданиях и проблемах, чтобы стать успешным в изучении математики!
Источники

Для более подробной информации о нахождении объема параллелепипеда вы можете обратиться к следующим ресурсам:
| Математическое бюро | – на этом сайте вы найдете подробное описание формул и примеры расчетов объема параллелепипеда. |
| Решалка | – здесь вы сможете найти примеры задач и их решения по нахождению объема параллелепипеда. |
| Mathprofi | – на этом сайте есть теоретические материалы и практические задачи для закрепления знаний о параллелепипеде. |