Правильная призма – это геометрическое тело, состоящее из двух равных и параллельных многоугольников в форме оснований и прямоугольных граней, соединяющих их. Она имеет свой собственный объем, который можно определить с помощью специальной формулы. Рассмотрим, как найти объем правильной призмы и решать задачи с ней.
Формула для расчета объема правильной призмы состоит из умножения площади основания на высоту призмы. Обозначим площадь основания как S, а высоту как h. Тогда формула будет выглядеть так: V = S * h.
Пример: Допустим, у нас есть правильная призма со стороной основания длиной 4 см и высотой 6 см. Сначала найдем площадь основания, вычислив площадь прямоугольника: S = 4 см * 4 см = 16 см². Затем умножим полученную площадь на высоту призмы: V = 16 см² * 6 см = 96 см³. Таким образом, объем этой призмы равен 96 кубическим сантиметрам.
Теперь, когда вы знаете, как найти объем правильной призмы, вы можете успешно решать задачи, связанные с этой геометрической фигурой.
Как найти объем правильной призмы?

Объем правильной призмы может быть вычислен с использованием простой формулы. Для того чтобы найти объем, нам понадобятся измерения длины, ширины и высоты призмы.
Формула для вычисления объема правильной призмы выглядит следующим образом:
Объем = Площадь основания × Высота
Где Площадь основания представляет собой площадь одной из плоских фигур, образующих основания призмы.
Например, если основание призмы является прямоугольником, то площадь основания вычисляется по формуле:
Площадь основания = Длина × Ширина
После того, как мы вычислили площадь основания, мы можем перемножить ее на высоту призмы, чтобы получить окончательный результат - объем призмы.
Таким образом, чтобы найти объем правильной призмы, следует умножить площадь основания на высоту.
Давайте рассмотрим пример:
У нас есть правильная призма с основанием в виде квадрата со стороной 5 см и высотой 10 см. Чтобы найти ее объем, мы должны сначала вычислить площадь основания:
Площадь основания = 5 см × 5 см = 25 см²
Затем мы умножаем площадь основания на высоту призмы:
Объем = 25 см² × 10 см = 250 см³
Полученный результат - 250 см³ - является объемом данной правильной призмы.
Что такое правильная призма?
У правильной призмы все боковые ребра и углы равны между собой. Она характеризуется высотой, которая является расстоянием между ее основаниями. В зависимости от формы оснований, правильные призмы могут быть треугольными, четырехугольными, пятиугольными и т. д.
Правильные призмы широко используются в геометрии, строительстве и других областях науки и техники. Их объем можно вычислить с использованием специальных формул, которые зависят от размеров призмы и ее формы. Правильная призма может быть как пустотелой, так и заполненной субстанцией – в этом случае ее объем будет зависеть от плотности материала, из которого она сделана.
Формула для нахождения объема
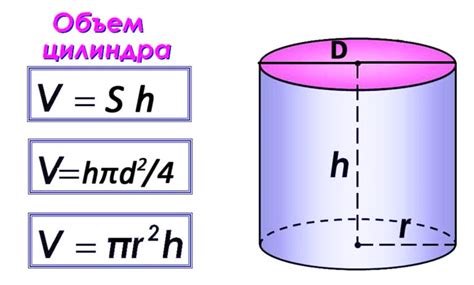
Объем правильной призмы можно вычислить, используя следующую формулу:
Объем = площадь основания * высота
Где:
- Площадь основания - это площадь поверхности основания призмы. Для различных форм основания, таких как квадрат, прямоугольник, треугольник или круг, площадь может быть вычислена по соответствующей формуле.
- Высота - это расстояние между основанием и противолежащей ему плоскостью призмы. Высота может быть измерена в сантиметрах, метрах или других единицах длины.
Например, если основание призмы является квадратом со стороной 5 см, а высота призмы равна 10 см, то объем можно вычислить следующим образом:
Объем = 5 см * 5 см * 10 см = 250 см³
Таким образом, объем этой призмы равен 250 кубическим сантиметрам.
Пример расчета объема

Для наглядности, рассмотрим пример расчета объема правильной призмы. Пусть у нас есть правильная треугольная призма с высотой 6 см и сторонами основания длиной 4 см, 5 см и 6 см.
Сначала найдем площадь основания призмы. Для этого воспользуемся формулой для площади треугольника: S = 1/2 * a * b * sin(C), где a, b - длины сторон основания, C - угол между этими сторонами.
В нашем случае, угол между сторонами 4 см и 5 см можно найти с помощью теоремы косинусов: C = arccos((a^2 + b^2 - c^2) / (2 * a * b)). Применяя данную формулу, найдем, что C ≈ 52.35 градуса.
Теперь, подставляя все значения в формулу для площади треугольника, получаем: S = 1/2 * 4 * 5 * sin(52.35 градуса) ≈ 9.66 см².
Наконец, умножим площадь основания на высоту, чтобы получить объем призмы: V = S * h = 9.66 см² * 6 см ≈ 57.96 см³.
Итак, объем данной призмы составляет примерно 57.96 см³.