Шар - одно из самых простых и красивых геометрических тел. У него нет ребер и граней, и он представляет собой идеально симметричную сферу. Важной характеристикой шара является его объем, который можно вычислить по радиусу. Если вы хотите узнать, как найти объем шара, то наша статья с примерами и пошаговой инструкцией вам поможет.
Определение объема шара очень важно во многих областях науки и техники. Например, зная объем шара, можно рассчитать его плотность, массу или площадь поверхности. Для решения этой задачи, нам понадобятся формулы и математические выкладки. Но не беспокойтесь, мы разберем все шаги по порядку и приведем примеры, которые помогут вам лучше понять этот процесс.
Формула для вычисления объема шара достаточно проста:
V = (4/3) × π × r³
где V - объем шара, π - число пи (приближенное значение равно 3,14), а r - радиус шара. Теперь, когда у нас есть формула, давайте рассмотрим несколько примеров, чтобы лучше понять, как ее применять.
Что такое объем шара?

Чтобы вычислить объем шара, необходимо знать его радиус - расстояние от центра шара до любой его точки. Формула для вычисления объема шара в зависимости от радиуса выглядит следующим образом:
V = (4/3) * π * r^3
Где V - объем шара, π (пи) - математическая константа, примерное значение которой равно 3,14, и r - радиус шара.
Вычисление объема шара может быть полезно в различных областях, включая геометрию, физику, инженерию и другие. Например, зная объем шара, можно определить его массу, если известна плотность материала, из которого он сделан. Также объем шара может использоваться для расчета вместимости сосудов, количества материалов при упаковке и многих других задач.
Радиус шара и его связь с объемом

Объем шара определяется формулой V = 4/3πr³, где V - объем, r - радиус, а π - это математическая константа, примерно равная 3,14159. Таким образом, зная значение радиуса, мы можем легко вычислить объем шара.
Радиус шара также имеет важное значение при решении различных задач. Например, при проектировании сферических объектов радиус может определяться исходя из требуемого объема. И наоборот, зная требуемый объем, мы можем найти соответствующий радиус.
Более того, радиус шара также влияет на его площадь поверхности. Площадь поверхности шара можно вычислить по формуле S = 4πr². Очевидно, что чем больше радиус, тем больше будет и площадь поверхности. Поэтому, увеличивая радиус шара, мы получаем не только больший объем, но и большую площадь поверхности.
Знание связи между радиусом шара и его объемом позволяет с легкостью решать различные задачи, связанные с этими характеристиками. Например, можно вычислить, на сколько процентов увеличится объем шара, если его радиус увеличится на определенное значение.
Формула для расчета объема шара
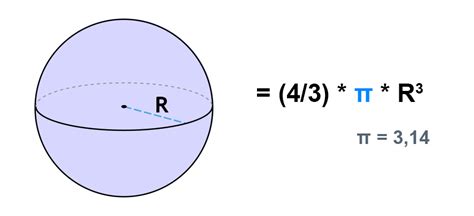
Объем шара можно рассчитать с помощью простой формулы. Представим, что у нас есть шар с заданным радиусом. Чтобы найти объем данного шара, нужно воспользоваться следующей формулой:
V = (4/3)πr³
где V - объем, π - математическая константа, равная приближенно 3,14, а r - радиус шара.
Для расчета объема шара, достаточно знать только его радиус. Используя данную формулу, можно быстро и точно найти объем шара и использовать эту информацию для различных целей.
Пример:
Пусть у нас есть шар с радиусом 5 см. Используя формулу для расчета объема шара, найдем его объем:
V = (4/3)πr³
V = (4/3) × 3.14 × 5³
V = (4/3) × 3.14 × 125
V ≈ 523.333 см³
Таким образом, объем шара с радиусом 5 см составляет приблизительно 523.333 см³.
Используя данную формулу и данные о радиусе, вы можете легко рассчитать объем шара для любого заданного радиуса.
Примеры расчета объема шара
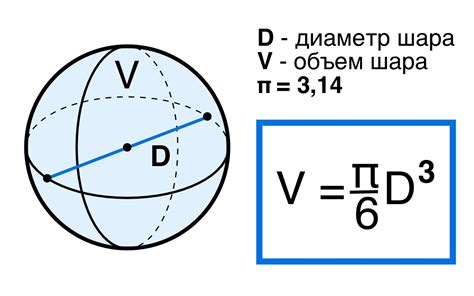
В этом разделе мы рассмотрим несколько практических примеров расчета объема шара по заданному радиусу.
| Пример | Радиус (r) | Объем (V) |
|---|---|---|
| Пример 1 | 5 см | 523.6 см³ |
| Пример 2 | 2 м | 33.5 м³ |
| Пример 3 | 10 дм | 4188.8 дм³ |
Для каждого примера мы указали значение радиуса шара и объем, рассчитанный с использованием соответствующей формулы. Эти примеры помогут вам лучше понять процесс расчета объема шара и практическое применение этой математической концепции.
Как найти объем шара на практике

Для вычисления объема шара по его радиусу необходимо знать формулу, а также уметь применять ее на практике. Этот процесс может показаться сложным, но на самом деле достаточно прост. Вот пошаговая инструкция:
- Сначала нужно вспомнить формулу для вычисления объема шара: V = (4/3) * π * r^3, где V - объем шара, π - число пи (приближенно равно 3.14159) и r - радиус шара.
- Теперь, когда у нас есть формула, можно перейти к вычислениям. Вместо переменных в формуле подставляем известные значения. Например, если радиус шара равен 5 см, то получаем следующее: V = (4/3) * 3.14159 * 5^3.
- Далее выполняем вычисления по правилам арифметики. Сначала возводим радиус в куб и умножаем на число пи, затем умножаем на 4/3. В результате получаем значение объема шара.
- В данном примере получаем следующий результат: V = (4/3) * 3.14159 * 125 ≈ 523.599 см³.
Таким образом, объем шара с радиусом 5 см составляет приблизительно 523.599 кубических сантиметра. Практическое применение этой формулы позволяет рассчитывать объем шара в различных ситуациях, таких как при изготовлении шаровых елок или определении объема шарообразных тел.
Единицы измерения объема шара

Однако, в некоторых случаях можно встретить более редко используемые единицы измерения, такие как кубические миллиметры (мм³) или литры (л). Кубический миллиметр - это объем, занимаемый кому-то шаром с радиусом в один миллиметр. Литр - это объем, равный одной тысячной доле кубического метра или 1000 кубическим сантиметрам.
Для более удобного использования дробных или очень крупных значений объема шара, также можно встретить единицы измерения в формате научных обозначений. Например, мегалитры (Мл) или микролитры (мкл). Мегалитр - это объем, равный одной миллионной доле кубического метра, а микролитр - это объем, равный одной миллионной доле кубического сантиметра.
При выборе единицы измерения объема шара следует учитывать конкретную ситуацию и требования задачи. Определение единицы измерения позволит получить более понятный и удобный результат.
Инструкция по расчету объема шара
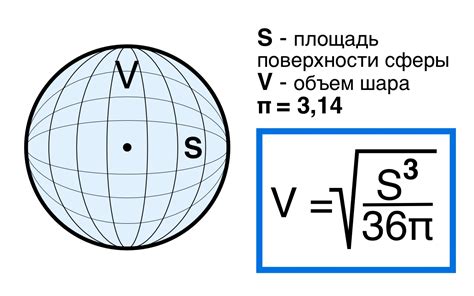
Шаг 2: Вспомните формулу для расчета объема шара. Объем V шара можно вычислить по формуле V = (4/3) * π * r³, где π - это число Пи, приближенно равное 3,14, а r - радиус шара.
Шаг 3: Подставьте известное значение радиуса шара в формулу для расчета объема. Убедитесь, что все значения заполнены правильно.
Шаг 4: Выполните необходимые вычисления. Возведите радиус в третью степень и умножьте результат на коэффициент (4/3) и число Пи (π).
Шаг 5: Ответ представьте в форме числа. Округлите результат до нужного количества знаков после запятой в соответствии с условиями задачи.
Например:
Пусть радиус шара равен 5 см.
V = (4/3) * 3,14 * (5³) = 4/3 * 3,14 * 125 = 4/3 * 392,5 = 1570 см³.
Шаг 6: Проверьте правильность своего ответа. Убедитесь, что полученный объем шара соответствует условию задачи и имеет правильные единицы измерения.
Теперь вы знаете, как рассчитать объем шара по заданному радиусу. Пользуйтесь этой инструкцией для решения любых задач, связанных с нахождением объема шара.
Применение объема шара в повседневной жизни

Знание объема шара может оказаться полезным в различных сферах нашей жизни. Рассмотрим несколько примеров, где мы можем использовать эту величину.
Архитектура и строительство: При проектировании зданий и сооружений важно знать объем объектов, чтобы правильно расчитать стоимость строительных материалов и объем работ. Например, при планировании спортивных комплексов или концертных залов можно использовать формулу для определения объема шара, чтобы рассчитать вместительность арены или объем воздуха, который необходим для создания комфортных условий для зрителей или слушателей.
Упаковка и хранение: Представим себе, что у нас есть шарики для игры в доме или в детском саду. Чтобы правильно подобрать коробку или сумку для хранения или транспортировки шаров, необходимо знать их объем. Также при решении задач связанных с упаковкой товаров в коробки иногда полезно знать объем шаров или шарообразных предметов, чтобы правильно оценить возможность упаковки и не допустить повреждений товаров.
Физика и наука: В физике и других научных дисциплинах объем шара используется при исследовании свойств материалов, расчетах объемов жидкостей или газов. Например, в метерологии объем атмосферы и облаков можно рассчитать, используя формулу для объема шара. Также, в медицине объемы внутренних органов могут быть рассчитаны с помощью формулы для объема шара, что поможет в диагностике и планировании хирургических вмешательств.
Таким образом, знание объема шара может оказаться полезным в самых различных ситуациях, где требуется рассчет объемных характеристик объектов или исследований.