Объем – одна из основных характеристик геометрических фигур, позволяющая определить, сколько пространства они занимают. Определение объема треугольника – задача не для новичков, но справиться с ней совсем несложно, если использовать соответствующие формулы.
Треугольник – это геометрическая фигура, состоящая из трех сторон и трех углов. Объем треугольника – это измерение трехмерной геометрической фигуры, и определить его можноемкость или объемовым содержанием треугольника.
Для вычисления объема треугольника существует специальная формула, которая зависит от формы треугольника и размеров его сторон. Для простоты рассмотрим формулы для нескольких типов треугольников.
Что такое объем треугольника?
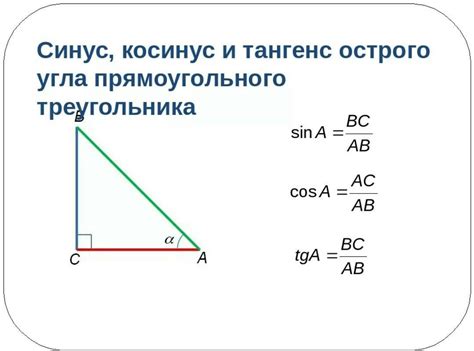
Треугольник – это геометрическая фигура, состоящая из трех сторон и трех углов. Он является одним из основных элементов геометрии и широко используется в различных областях науки, техники и искусства.
Однако, объем треугольника как такового не существует, поскольку треугольник является плоской фигурой и не имеет объема. Объем применим к трехмерным фигурам, таким как параллелепипеды, цилиндры или конусы.
Тем не менее, треугольник может быть составной частью трехмерной фигуры, например, пирамиды или призмы. В таком случае, если треугольник является основанием или боковой стороной трехмерной фигуры, то можно рассчитать объем этой фигуры.
Для расчета объема трехмерной фигуры с треугольником использованы специальные формулы, которые учитывают размеры и форму треугольника, а также высоту и другие параметры трехмерной фигуры.
Объем треугольника является одним из ключевых понятий геометрии, позволяющим нам изучать и анализировать трехмерные объекты и пространство вокруг нас.
Формула для расчета объема треугольника
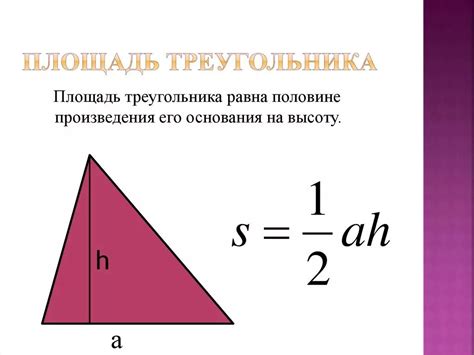
Объем треугольника может быть рассчитан с использованием формулы для объема пирамиды.
Формула для объема пирамиды имеет вид:
V = (S * h) / 3
где:
V - объем пирамиды или треугольника
S - площадь основания треугольника
h - высота треугольника
Для расчета объема треугольника необходимо знать площадь его основания и высоту.
Площадь основания треугольника можно найти с помощью формулы:
S = (a * b * sin(C)) / 2
где:
a и b - длины сторон треугольника
C - угол между этими сторонами
Высоту треугольника можно найти с помощью различных методов, в зависимости от задачи.
Используя эти формулы, можно рассчитать объем треугольника и использовать его для различных целей, например при проектировании или строительстве.
Как найти основание треугольника
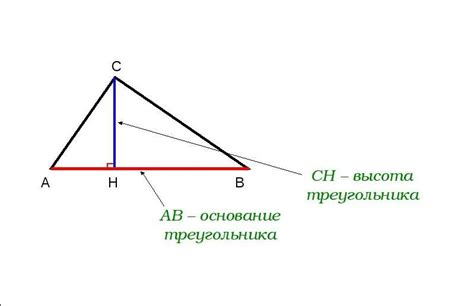
Есть несколько способов найти основание треугольника, в зависимости от доступных данных:
1. Зная высоту и площадь треугольника:
Если у вас есть информация о высоте и площади треугольника, то вы можете использовать формулу для нахождения основания:
Основание треугольника = (2 × площадь треугольника) / высота треугольника
2. Зная длины других сторон треугольника:
Если у вас есть информация о длине двух сторон треугольника и угле между ними, то вы можете использовать теорему косинусов для нахождения длины третьей стороны треугольника. Затем, используя формулу для площади треугольника, вы можете найти высоту. После этого, основание треугольника будет легко найти, используя формулу из предыдущего способа.
3. Зная координаты вершин треугольника:
Если у вас есть информация о координатах вершин треугольника, то вы можете использовать формулу для расстояния между двумя точками в декартовой системе координат. Применяя эту формулу для каждой из сторон треугольника, вы найдете их длины. Затем, используя формулу для площади треугольника, вы можете найти высоту. После этого, основание треугольника будет легко найти, используя формулу из первого способа.
Найдя основание треугольника, вы сможете решать задачи, связанные с его геометрическими характеристиками и применять его для нахождения других величин, связанных с этим треугольником.
Как найти высоту треугольника
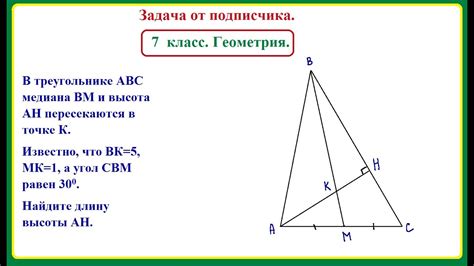
Существует несколько способов нахождения высоты треугольника, в зависимости от известных данных:
1. Известны площадь и основание треугольника:
Высоту треугольника можно найти, используя формулу:
Высота = 2 * (Площадь треугольника) / (Основание треугольника)
2. Известны стороны треугольника:
Если известны длины всех сторон треугольника, то высота может быть найдена с использованием формулы Герона и правила Герона:
Высота = (2 * Площадь треугольника) / (Сумма длин сторон треугольника)
3. Известны две стороны треугольника и угол между ними:
Высота треугольника может быть найдена, используя формулу:
Высота = (Одна сторона треугольника) * sin(Угол между сторонами)
Используя эти формулы, вы сможете находить высоту треугольника в различных ситуациях. Убедитесь, что входные данные правильно распознаны и вы правильно применяете соответствующую формулу для нахождения высоты треугольника в конкретном случае.
Как применить формулу для расчета объема треугольника
Расчет объема треугольника основан на использовании специальной формулы, которая позволяет найти объем фигуры. В отличие от прямоугольной или круглой формы, треугольник требует некоторых дополнительных шагов для вычисления его объема. В этой статье мы рассмотрим, как применить формулу для расчета объема треугольника.
Для начала, нам необходимо знать три параметра треугольника: его площадь основы, высоту и длину одной из его граней. Объем треугольника вычисляется с использованием следующей формулы:
Объем = (Площадь основы * Высоту) / 3
Для начала, нам нужно найти площадь основы треугольника. Это можно сделать, умножив длину основы на половину основы, то есть:
Площадь основы = (Длина основы * Высота основания) / 2
Затем мы можем использовать найденную площадь основы и высоту, чтобы найти объем треугольника, подставив эти значения в первую формулу.
Важно помнить, что все значения должны быть измерены в одной и той же системе измерения, например, в метрах или сантиметрах. Если значения измерены в разных единицах, их следует привести к общей системе измерения перед проведением расчетов.
Теперь вы знаете, как применить формулу для расчета объема треугольника. Не забывайте учитывать все необходимые параметры и проводить расчеты в соответствии с указанной формулой. Это поможет вам быстро и точно определить объем треугольника и использовать эту информацию для нужд вашего проекта.