Физика – это один из самых интересных и практически значимых предметов в школьной программе. Она позволяет понять, как устроен наш мир и объясняет множество явлений, с которыми мы сталкиваемся в повседневной жизни. Одним из важных понятий в физике является объем. Знание формулы, позволяющей найти объем, поможет решить множество задач и заданий на уроке.
Объем – это физическая величина, которая обозначает, сколько места занимает тело или вещество. Он измеряется в кубических метрах (м3) или иных кубических единицах. Научиться находить объем – задача несложная, если знать соответствующую формулу.
В 7 классе особое внимание уделяется различным геометрическим формам, таким как параллелепипеды, призмы и пирамиды. Для каждой из этих фигур существуют отдельные формулы для нахождения объема. Зная эти формулы, вы сможете решить задания и задачи, требующие вычисления объема.
Задача физики в 7 классе

Одной из задач, которая может быть предложена в 7 классе, является расчет объема тела. Для этого ученику нужно знать соответствующую формулу и уметь ее применять.
Формула для расчета объема тела может быть различной в зависимости от его формы. Например, для прямоугольного параллелепипеда объем можно вычислить по формуле:
V = l * w * h
Где V - объем тела, l - длина, w - ширина, h - высота.
Другие формулы расчета объема могут быть использованы для различных тел, таких как сфера, цилиндр или конус. Важно понимать, что каждой форме соответствует своя формула.
Решая задачи по физике в 7 классе, ученики не только развивают понимание физических законов, но и применяют математические навыки для решения простых уравнений. Это помогает им развивать логическое мышление и аналитические способности.
Таким образом, задачи по физике в 7 классе способствуют развитию учеников и помогают им лучше понять мир, окружающий нас.
Объем в физике: что это и как его найти

В физике существуют различные способы и формулы для вычисления объема в зависимости от формы тела. Например, для прямоугольного параллелепипеда можно использовать формулу:
Объем = длина x ширина x высота
Для сферы формула будет выглядеть так:
Объем = (4/3) x π x радиус³
Для других геометрических фигур существуют свои уникальные формулы для расчета объема. Например, для цилиндра:
Объем = π x радиус² x высота
Или для конуса:
Объем = (1/3) x π x радиус² x высота
Важно помнить, что при использовании формулы для вычисления объема необходимо работать с соответствующими размерами в нужных единицах измерения – например, сантиметрами или метрами – чтобы получить верный результат.
Теперь, когда ты знаешь, что такое объем и как его найти, ты сможешь успешно решать задачи по физике, связанные с этой величиной.
Формула для вычисления объема
Одна из наиболее простых формул для вычисления объема применяется для прямоугольного параллелепипеда. Объем V такого тела можно найти, умножив длину l, ширину w и высоту h:
V = l * w * h
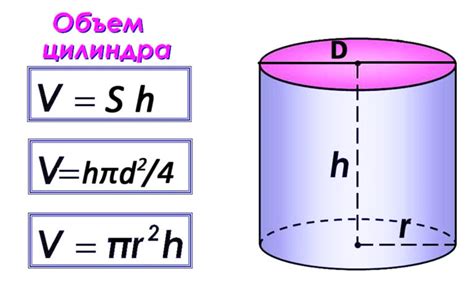
Для вычисления объема цилиндра, необходимо знать его радиус r и высоту h. Формула для вычисления объема цилиндра:
V = π * r2 * h,
где π (пи) представляет собой математическую константу, примерное значение которой составляет 3,14.
Если нужно найти объем шара, достаточно знать его радиус r. Формула для вычисления объема шара:
V = (4/3) * π * r3.
Необходимо выбрать формулу, соответствующую геометрической фигуре, для которой надо найти объем.
Учебное задание по нахождению объема
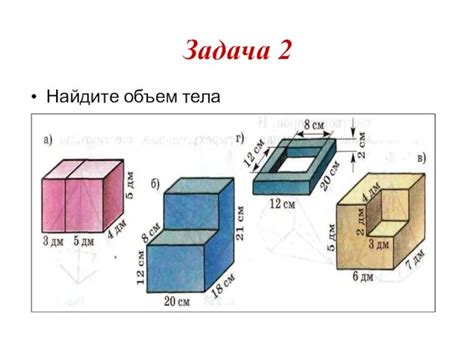
В данном учебном задании вам предстоит решить несколько примеров на нахождение объема различных тел. Для этого необходимо использовать соответствующие формулы и подставить в них известные значения.
Пример задания:
| № | Тело | Известные значения | Формула для нахождения объема |
|---|---|---|---|
| 1 | Цилиндр | Радиус основания: 3 см Высота: 5 см | V = πr²h |
| 2 | Параллелепипед | Длина: 7 см Ширина: 4 см Высота: 2 см | V = lwh |
| 3 | Сфера | Радиус: 10 см | V = 4/3πr³ |
При решении задания помните о необходимости указания единиц измерения в ответе. Также обращайте внимание на правильность подстановки значений в формулы и правильность выполнения вычислений.
Успешное выполнение этого учебного задания поможет вам лучше разобраться в понятии объема и применении соответствующих формул для различных тел.
Примеры заданий

1. Найдите объем прямоугольного параллелепипеда с длиной сторон a = 5 см, шириной b = 3 см и высотой h = 10 см.
| Дано: | Искомое: |
|---|---|
| Длина стороны a: 5 см | Объем V: |
| Ширина стороны b: 3 см | |
| Высота h: 10 см |
2. Куб имеет ребро длиной a = 6 см. Найдите его объем.
| Дано: | Искомое: |
|---|---|
| Длина ребра a: 6 см | Объем V: |
3. Найдите объем цилиндра, если его радиус основания r = 2 см, а высота h = 8 см.
| Дано: | Искомое: |
|---|---|
| Радиус основания r: 2 см | Объем V: |
| Высота h: 8 см |
4. Найдите объем шара с радиусом r = 4 см.
| Дано: | Искомое: |
|---|---|
| Радиус r: 4 см | Объем V: |
Практическое применение знания объема

Знание объема имеет практическое применение во многих областях нашей жизни. Оно позволяет решать задачи в повседневных ситуациях и в различных научных и технических областях.
В строительстве, например, знание объема позволяет оценить количество материалов, необходимых для постройки здания или сооружения. Это важно для планирования бюджета и ресурсов.
В торговле и логистике знание объема помогает определить, сколько товаров поместится в определенный контейнер или транспортное средство. Это позволяет оптимизировать процессы хранения и доставки товаров и экономить на затратах.
В медицине объем имеет большое значение для диагностики и лечения. Например, при проведении Томографических исследований (КТ, МРТ) объем используется для определения размеров органов и опухолей, что позволяет врачам выявлять и лечить различные заболевания.
Также знание объема используется в процессе проектирования и изготовления различных предметов декора, мебели и других изделий, где требуется точное определение объема для создания правильной формы и размеров.
Знание объема является ключевым элементом в практической применимости физики и математики в различных сферах нашей жизни, играет важную роль в нашем повседневном опыте и позволяет нам более точно и эффективно решать различные задачи.
Примеры использования в жизни

| Область | Пример использования |
|---|---|
| Строительство | При планировании строительства жилого дома, необходимо знать объем материалов, таких как бетон, кирпичи или дерево, чтобы правильно рассчитать их количество и смету. |
| Транспорт | При проектировании грузовых контейнеров или судов, необходимо учесть объем, чтобы определить максимальную грузоподъемность и обеспечить безопасную перевозку товаров. |
| Медицина | При расчете дозировки лекарственных препаратов, врачи учитывают объем тела пациента, чтобы правильно определить необходимое количество лекарств. |
| Химия | При проведении химических реакций, объем используется для определения концентрации растворов и расчета стехиометрических коэффициентов. |
| Торговля | При расчете стоимости товара, объем может быть использован для определения цены единицы товара или упаковки. |
Это лишь некоторые примеры, демонстрирующие важность понимания и применения понятия объема в различных аспектах нашей жизни!