В геометрии понятие объема фигуры играет важную роль и применяется в различных областях, таких как строительство, инженерия, архитектура и дизайн. Знание способов нахождения объема позволяет эффективно решать задачи, связанные с определением размеров тела и его заполнения. Для разных фигур применяются разные методы расчета. В этой статье мы рассмотрим простые способы и формулы для нахождения объема различных фигур.
Один из самых простых способов найти объем фигуры – использовать соответствующую формулу. Формулы для нахождения объема различных фигур можно легко найти в учебниках по математике или геометрии. Например, для нахождения объема прямоугольного параллелепипеда нужно умножить длину на ширину на высоту:
V = a * b * h
где V – объем, a – длина, b – ширина, h – высота. Есть и другие формулы для нахождения объема таких фигур, как сфера, цилиндр, конус и т. д.
Еще одним способом нахождения объема фигуры является метод геометрического моделирования. Здесь требуется создать модель фигуры из бумаги, картона, пластилина или других материалов и затем ее измерить. Этот метод может быть особенно полезен для необычных или сложных фигур, для которых нет простой формулы для расчета объема. Однако, этот способ требует больше времени и усилий, чем использование формулы.
Методы и формулы для нахождения объемов различных фигур
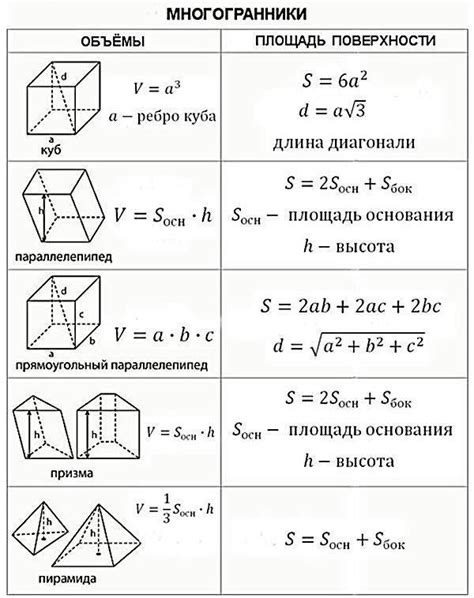
Вот некоторые из основных методов и формул для нахождения объемов различных фигур:
- Для прямоугольного параллелепипеда: V = a * b * c, где a, b и c – длины его сторон.
- Для куба: V = a^3, где a – длина его стороны.
- Для цилиндра: V = π * r^2 * h, где r – радиус основания, а h – высота.
- Для конуса: V = (1/3) * π * r^2 * h, где r – радиус основания, а h – высота.
- Для сферы: V = (4/3) * π * r^3, где r – радиус.
Это лишь некоторые из формул, с помощью которых можно вычислить объемы различных фигур. При решении задач обязательно учитывайте все данные, которые имеются, и внимательно применяйте соответствующую формулу.
Не забывайте также о переводе единиц измерения и точности вычислений, особенно при использовании формул, в которых встречается числовой коэффициент, например, π или 1/3. Возможные ошибки в переводе или округлении могут существенно повлиять на результат.
Как найти объем куба с помощью формулы

Формула для нахождения объема куба: V = a^3, где V - объем куба, а - длина одного из его ребер.
Давайте разберемся, как использовать эту формулу на примере.
| Значение ребра (a) | Объем (V) |
|---|---|
| 3 | 27 |
| 4 | 64 |
| 5 | 125 |
| 6 | 216 |
Таким образом, чтобы найти объем куба, необходимо знать длину одного из его ребер и возвести ее в куб. Результатом будет объем куба.
Простой способ расчета объема параллелепипеда
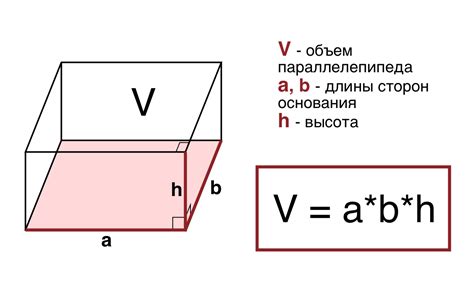
Для определения объема параллелепипеда достаточно знать длину (a), ширину (b) и высоту (c) данной фигуры. Формула для расчета объема параллелепипеда проста:
V = a * b * c
Где V - объем параллелепипеда, а, b и c - длина, ширина и высота соответственно.
Найдя значения длины, ширины и высоты параллелепипеда, подставьте их в формулу и выполните простые арифметические операции. В результате, вы получите объем данной фигуры.
Таким образом, расчет объема параллелепипеда - это достаточно простая операция. С помощью данной формулы легко определить, сколько объема занимает данный объект.
Формула нахождения объема цилиндра
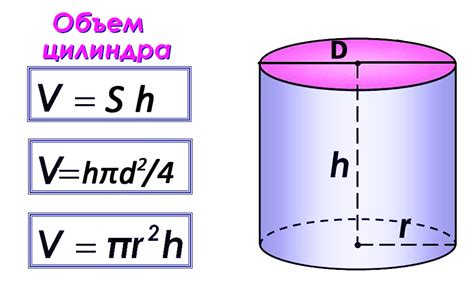
Формула для нахождения объема цилиндра представляет собой умножение площади основания на высоту:
| Обозначение | Параметр цилиндра |
| S | Площадь основания |
| h | Высота цилиндра |
| V | Объем цилиндра |
Таким образом, формула для нахождения объема цилиндра записывается следующим образом:
V = S * h
Где S - площадь основания, а h - высота цилиндра.
Теперь, зная формулу нахождения объема цилиндра, вы можете легко вычислить объем данной фигуры.
Как определить объем пирамиды за несколько шагов

- Запишите известные данные. Для определения объема пирамиды необходимо знать ее высоту и площадь основания. Убедитесь, что данные параметры измерены в одной системе единиц.
- Используйте формулу. Объем пирамиды может быть определен с помощью формулы:
V = (1/3) * S * h, где V - объем, S - площадь основания, h - высота. Учтите, что площадь основания может быть разной формы, например, прямоугольником или треугольником. - Подставьте значения в формулу. Замените символы V, S и h на соответствующие значения. Удостоверьтесь, что единицы измерения согласуются.
- Выполните вычисления. Умножьте площадь основания на высоту, а затем умножьте результат на 1/3. Полученное число и будет являться объемом пирамиды.
Например, допустим, у нас есть пирамида с площадью основания 10 квадратных метров и высотой 5 метров. Для определения объема воспользуемся формулой:
V = (1/3) * 10 * 5 = 16.67 кубических метра.
Таким образом, объем данной пирамиды будет составлять 16.67 кубических метра.
Используя представленные шаги, вы сможете определить объем пирамиды с легкостью. Помните, что правильное определение объема является важным фактором при работе с трехмерными фигурами.
Методы расчета объема конуса: простые и точные формулы
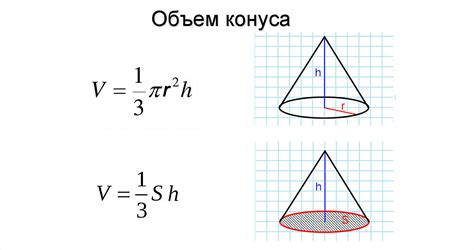
Один из самых простых и широко используемых методов - это использование формулы для объема конуса:
| Формула | Описание |
| V = (1/3) * π * r^2 * h | Формула объема конуса, где V - объем, π - число Пи (приближенно равно 3.14), r - радиус основания, h - высота. |
Применение этой формулы требует знания радиуса основания и высоты конуса. Если необходимо определить объем конуса, используя другие известные параметры, могут потребоваться более точные и сложные методы расчета.
Если известны диаметр основания и высота конуса, можно воспользоваться слегка измененной формулой:
| Формула | Описание |
| V = (1/6) * π * d^2 * h | Формула объема конуса при известном диаметре основания, где V - объем, π - число Пи (приближенно равно 3.14), d - диаметр основания, h - высота. |
Если известна лишь длина окружности основания, можно воспользоваться следующей формулой:
| Формула | Описание |
| V = (C^2 * h) / (12 * π) | Формула объема конуса при известной длине окружности основания, где V - объем, C - длина окружности основания, h - высота. |
Важно помнить, что для всех этих формул необходимо правильно измерять и подставлять значения радиуса, диаметра, высоты и длины окружности согласно выбранной системе измерений (например, сантиметры, метры и т.д.).
Какой метод используется для расчета объема конуса, зависит от доступных данных и необходимой точности результатов. В реальных задачах может потребоваться комбинирование разных методов или использование более сложных формул для получения более точного результата.
Нахождение объема сферы: формула и алгоритм действий

Формула для нахождения объема сферы:
V = (4/3) * π * r³
где V - объем сферы, π (пи) - математическая константа, приближенное значение которой равно 3.14159, r - радиус сферы. Данная формула основывается на том, что при вращении полуокружности вокруг ее диаметра происходит образование сферы.
Алгоритм действий для нахождения объема сферы:
- Запишите значение радиуса сферы.
- Возводите значение радиуса в куб.
- Умножьте результат из пункта 2 на число π (пи), вычислив его значение с необходимой точностью.
- Умножьте результат из пункта 3 на 4/3.
- Полученное число является объемом сферы.
Например, если радиус сферы равен 5, то для нахождения объема сферы можно использовать следующий алгоритм:
- Радиус в куб: 5 * 5 * 5 = 125.
- Умножение на π: 125 * 3.14159 = 392.699.
- Умножение на 4/3: 392.699 * 4/3 = 523.598.
Таким образом, для сферы с радиусом 5, объем будет равен 523.598.
Используя данную формулу и алгоритм, вы можете легко находить объем сферы, имея только значение радиуса. Это очень полезно в решении задач и практических ситуаций связанных с геометрией и физикой.