Область определения функции является одним из важных понятий в математике. Она позволяет определить все значения, при которых функция принимает смысловую природу и не имеет различных ограничений.
Одним из методов определения области определения функций является анализ дискриминанта. Дискриминант - это математическое выражение, которое позволяет найти корни квадратного уравнения. В случае функции, содержащей квадратный корень, дискриминант помогает найти значения, при которых функция имеет смысловую природу.
Для определения области определения функции с использованием дискриминанта необходимо анализировать его значение. Если дискриминант положителен, то функция имеет корни и может быть определена при любых значениях аргумента. Если дискриминант равен нулю, то функция имеет один корень и имеет смысловую природу при определенных значениях аргумента. Если же дискриминант отрицателен, то функция не имеет корней и при данных значениях аргумента не имеет смысловой природы.
Определение области определения

Чтобы определить область определения функции, необходимо учитывать различные ограничения, которые могут быть наложены на функцию. Например, функция может содержать знаменатель, который не может быть равен нулю, или аргумент под корнем должен быть неотрицательным. В таких случаях необходимо определить множество значений независимой переменной, которые удовлетворяют этим ограничениям.
Область определения функции может быть представлена в виде таблицы, где представлены различные ограничения и соответствующие им значения независимой переменной. Например:
| Ограничение | Значение независимой переменной |
|---|---|
| Знаменатель не равен нулю | Все значения, кроме нуля |
| Аргумент под корнем неотрицателен | Значения больше или равные нулю |
Зная область определения функции, мы можем более точно определить ее поведение и провести дальнейшие исследования функции, такие как нахождение значений функции, нахождение суммы или разности функций и т.д.
Что такое область определения

Когда мы говорим о функции, мы имеем в виду математическую функцию, которая связывает элементы одного множества (аргументы) с элементами другого множества (значения). Область определения функции определяет, какие аргументы являются допустимыми в контексте этой функции.
Например, функция f(x) = √x определена только для неотрицательных значений x, так как квадратный корень из отрицательного числа не имеет смысла в контексте обычных действительных чисел. Поэтому, область определения этой функции состоит из всех неотрицательных чисел.
Область определения может иметь различные формы, включая интервалы, полуинтервалы, объединение нескольких интервалов или все действительные числа. Она зависит от специфики функции и условий, которые необходимо удовлетворять для ее применения.
Знание области определения функции важно при решении уравнений и неравенств, анализе интервалов возрастания и убывания функции, определении ее графика и других математических операциях.
Важно помнить, что область определения функции может быть ограничена из-за различных физических или математических ограничений, с которыми мы сталкиваемся в реальном мире.
Зачем нужно знать область определения

Одной из основных причин знания области определения является избегание ошибок при вычислении функции. Если значение, для которого вы хотите вычислить функцию, не принадлежит ее области определения, то результат будет неопределенным или даже ошибочным.
Также знание области определения помогает в анализе и изучении функции. Изучение области значений функции может помочь понять поведение функции на разных участках и установить особенности ее графика.
Область определения также важна при решении уравнений и неравенств, содержащих функции. При решении таких уравнений или неравенств необходимо учитывать область определения функции, чтобы исключить значения, не являющиеся допустимыми в контексте задачи.
Наконец, знание области определения функции позволяет избежать деления на ноль. Если значение переменной попадает в зону неопределенности функции, то это может привести к ошибке или некорректным решениям задачи.
Таким образом, знание области определения функции необходимо для правильного вычисления функций, анализа и изучения их свойств, решения уравнений и неравенств, а также избежания ошибок и некорректных результатов.
Дискриминант функции

В общем виде дискриминант функции представляет собой выражение, которое исходит из уравнения функции и определяет его свойства. Дискриминант позволяет понять, какие значения аргумента могут быть подставлены в функцию, чтобы получить решение. Если дискриминант меньше нуля, значит, функция не имеет решений на множестве действительных чисел. Если дискриминант равен нулю, то функция имеет единственное решение. Если дискриминант больше нуля, то функция имеет два различных решения.
Для квадратных уравнений дискриминант функции вычисляется по формуле: Д = b² - 4ac, где a, b, c – коэффициенты уравнения. Значение дискриминанта позволяет судить о количестве и типе решений квадратного уравнения.
Определение области определения функции с помощью дискриминанта является важной задачей в математике и используется для установления свойств и особенностей функций различных типов. Знание дискриминанта позволяет более точно и полно описывать функции и исследовать их поведение.
Что такое дискриминант функции

Дискриминант функции обычно обозначается символом Δ (дельта) и рассчитывается по формуле, зависящей от типа функции. Наиболее распространенными случаями являются квадратные и уравнения второй степени.
Для квадратного уравнения вида ax^2 + bx + c = 0, дискриминант рассчитывается по формуле Δ = b^2 - 4ac. Значение дискриминанта позволяет определить, сколько корней имеет уравнение и какова их природа.
| Значение Δ | Количество корней | Тип корней |
|---|---|---|
| Δ > 0 | 2 | Два различных вещественных корня |
| Δ = 0 | 1 | Один вещественный корень |
| Δ | 0 | Нет вещественных корней |
Значение дискриминанта также влияет на форму графика функции. Если Δ > 0, то график функции пересекает ось x в двух различных точках. Если Δ = 0, то график функции касается оси x в одной точке. А если Δ
Как найти дискриминант функции
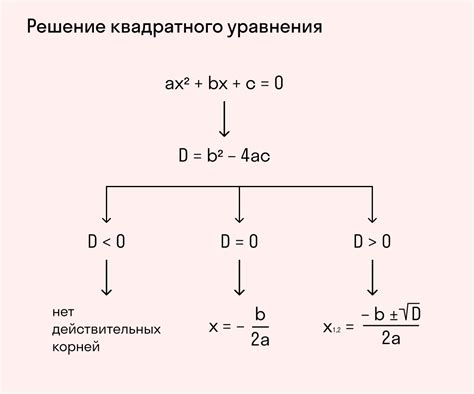
Для нахождения дискриминанта функции необходимо использовать специальную формулу, которая может отличаться в зависимости от типа функции. Например, для квадратной функции вида f(x) = ax^2 + bx + c дискриминант вычисляется по формуле D = b^2 - 4ac.
Знание значения дискриминанта позволяет определить область определения функции. Если значение дискриминанта положительное, то функция имеет два действительных корня и определена на всей числовой прямой. Если значение равно нулю, то функция имеет один действительный корень и также определена на всей числовой прямой. В случае, когда значение дискриминанта отрицательное, функция не имеет действительных корней и определена только на некотором интервале.
Также, знание значения дискриминанта позволяет найти точки экстремума функции. Если значение дискриминанта положительное, то функция имеет два минимума или два максимума. Если значение дискриминанта равно нулю, то функция имеет одну точку экстремума. В случае, когда значение дискриминанта отрицательное, функция не имеет точек экстремума.
Важно помнить, что дискриминант функции может быть не только числовым значением, но и выражением с переменными. В этом случае, область определения функции будет зависеть от значений переменных, аналогично числовой ситуации.
При нахождении дискриминанта функции необходимо учитывать условия, при которых функция может иметь мнимые корни или точки экстремума. В таких случаях необходимо использовать комплексные числа и специальные методы нахождения корней и экстремумов функции.
Шаги поиска области определения
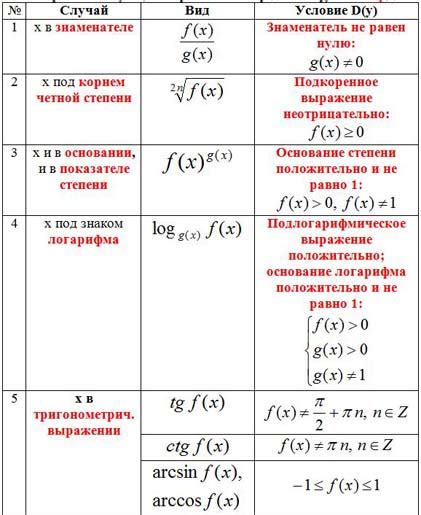
Для поиска области определения функции с использованием дискриминанта, нужно выполнить следующие шаги:
- Записать функцию в виде формулы, например:
- Найти значение дискриминанта функции, используя формулу:
- Рассмотреть различные случаи в зависимости от значения дискриминанта:
f(x) = ax2 + bx + c
D = b2 - 4ac
- Если дискриминант больше нуля, то функция определена при любом значении аргумента x.
- Если дискриминант равен нулю, то функция определена при всех значениях x.
- Если дискриминант меньше нуля, то функция не определена ни при каком значении x.
Зная различные случаи и значения дискриминанта, можно определить область определения функции и изучить её поведение.