Область определения функции - это множество значений аргумента, при которых функция имеет определенное значение. В математике область определения полностью определяет, какие значения аргумента можно подставить в функцию, чтобы получить корректный результат. Нахождение области определения является неотъемлемой частью анализа функций и позволяет определить особенности исследуемой функции.
Процесс нахождения области определения функции включает в себя несколько шагов. Во-первых, нужно исключить из рассмотрения значения аргумента, при которых функция имеет разрывы или не существует. Например, в случае рациональной функции необходимо исключить значения аргумента, при которых знаменатель функции равен нулю.
Кроме того, нужно учесть возможные ограничения на значения аргумента, которые могут быть указаны в условии задачи или в пределах рассматриваемого диапазона. Например, если задача говорит о нахождении области определения функции вещественного числа, необходимо исключить значения аргумента, при которых функция принимает комплексные значения.
Важно отметить, что в некоторых случаях область определения функции может быть ограничена и определяться условиями задачи или самой функции. Например, в случае логарифмической функции, аргумент должен быть строго положительным числом. Таким образом, при решении задачи нахождения области определения необходимо учитывать эти дополнительные условия и ограничения.
Определение и значение области определения функции

Для того чтобы найти область определения функции, необходимо учесть следующие ограничения:
| Ограничение | Значение |
|---|---|
| Деление на ноль | Функция не определена, если в знаменателе присутствует ноль. |
| Квадратный корень | Функция не определена, если под знаком квадратного корня находится отрицательное число. |
| Логарифм | Функция не определена, если аргумент логарифма меньше или равен нулю. |
Другие ограничения могут присутствовать в зависимости от конкретного уравнения или задачи. Например, функция может быть неопределена при наличии отрицательных значений в радикале, или при некоторых других условиях, указанных в задаче.
Зная область определения функции, можно провести анализ ее поведения и применять различные методы решения и оптимизации в задачах математики, физики, экономики и других наук.
Важность знания области определения функции

Правильное определение области определения функции позволяет избегать ошибок и неправильных результатов при работе с функцией. Это особенно важно в контексте математических моделей и приложений, где точность и надежность являются ключевыми требованиями.
Знание области определения также позволяет определить поведение функции на границах этой области. Например, если функция не определена в некоторой точке, это может быть связано с разрывом функции или несуществованием значения функции в этой точке. Эта информация важна для анализа функции и понимания ее свойств.
Как найти область определения функции по уравнению

Первым шагом определения области определения является нахождение корней уравнения. Для этого приравняем уравнение к нулю и решим его. Таким образом, мы найдем значения аргумента, при которых функция обращается в ноль.
Далее, необходимо проверить отрицательность внутри квадратных корней. Если в уравнении есть выражение под квадратным корнем, то это выражение должно быть неотрицательным, чтобы функция была определена для всех значений аргумента.
Наконец, если в уравнении есть знаменатель функции, необходимо учесть, что знаменатель не может быть равным нулю, так как деление на ноль неопределено. Поэтому мы исключаем из области определения значения аргумента, при которых знаменатель становится равным нулю.
В результате анализа всех этих факторов получаем область определения функции по уравнению. Эта область будет представлять собой интервалы значений аргумента, в которых функция определена.
Шаги по нахождению области определения функции
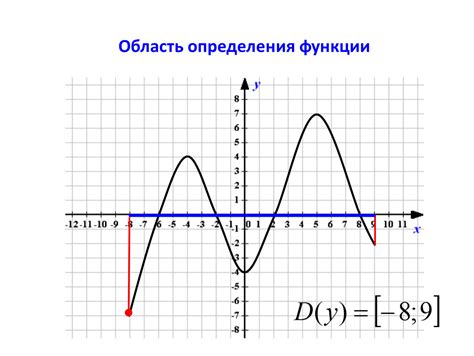
- Исследуйте все аргументы функции и определите, при каких значениях аргументы могут принимать реальные числа.
- Исключите значения аргументов, при которых функция делится на ноль или использует запрещенные операции, такие как извлечение корня из отрицательного числа или деление на ноль.
- Определите, существуют ли ограничения на значения аргументов, например, ограничение на значение функции или наличие знака внутри квадратного корня.
В каждом шаге важно правильно исследовать свойства функции и аргументы, чтобы исключить значения, при которых функция не имеет смысла или не может быть определена.
Примеры нахождения области определения функции

Рассмотрим несколько примеров нахождения области определения функции:
- Функция вида f(x) = \frac{1}{x}. Чтобы найти область определения, нужно исключить значения переменной x, при которых знаменатель равен нулю, так как деление на ноль не определено. Область определения этой функции будет множеством всех действительных чисел, кроме нуля: D(f) = (-\infty, 0) \cup (0, +\infty).
- Функция вида f(x) = \sqrt{x}. Чтобы найти область определения, нужно исключить значения переменной x, при которых аргумент под корнем отрицательный, так как корень из отрицательного числа не определен в множестве действительных чисел. Область определения этой функции будет множеством неотрицательных чисел: D(f) = [0, +\infty).
- Функция вида f(x) = \log{x}. Чтобы найти область определения, нужно исключить значения переменной x, при которых аргумент логарифма отрицателен или равен нулю, так как логарифм не определен для этих значений. Область определения этой функции будет множеством положительных чисел: D(f) = (0, +\infty).
Это лишь несколько примеров нахождения области определения функции. В каждом случае нужно анализировать уравнение функции и исключать значения переменной, при которых функция теряет смысл или не определена.
Полное руководство

Ниже представлено полное руководство по нахождению области определения функции по уравнению.
- Прочитайте уравнение и выявите все переменные, используемые в функции.
- Исключите все значения переменных, которые могут привести к делению на ноль или извлечению квадратного корня из отрицательного числа.
- Исключите все значения переменных, которые могут не удовлетворять другим ограничениям в уравнении, например, логарифму отрицательного числа или арксинусу, выходящему за пределы диапазона значений.
- Исключите все значения переменных, которые могут привести к бесконечному значению или отсутствию решения функции, например, в случае, когда основание логарифма равно единице.
- Составьте список всех оставшихся значений переменных. Это будет область определения функции.
После завершения этого руководства вы сможете определить область определения функции по ее уравнению и быть увереным в том, что все значения переменных, которые будут вводиться в функцию, удовлетворяют ее ограничениям и правилам.
Дополнительные полезные советы и подсказки

При нахождении области определения функции по уравнению стоит обратить внимание на следующие моменты:
1. Избегайте деления на ноль: Если у вас в уравнении функции есть знаменатель, то область определения не должна включать значения, при которых знаменатель равен нулю. Такие значения приводят к делению на ноль, что противоречит определению функции.
2. Извлечение корня: Если в уравнении функции есть извлечение корня, то область определения должна включать только значения, при которых подкоренное выражение неотрицательно. В противном случае, извлечение корня будет возвращать комплексные числа, что может противоречить определению функции.
3. Логарифмы: Если в уравнении функции есть логарифмы, то область определения должна включать только значения, при которых аргумент логарифма положителен. В противном случае, логарифм не будет иметь смысла, так как не определен для отрицательных или нулевых аргументов.
4. Квадратные корни: Если в уравнении функции присутствуют квадратные корни, то область определения должна включать только значения, при которых выражение под корнем неотрицательно. В противном случае, квадратный корень будет возвращать комплексные числа, что может противоречить определению функции.
Учитывая вышеперечисленные моменты, вы сможете более точно определить область определения функции по уравнению и избежать возможных ошибок.