Обратная функция - это функция, которая позволяет найти исходное значение, если известно значение функции. То есть, если для некоторого x функция f(x) дает нам y, то обратная функция f^-1(y) позволяет найти x.
Поиск обратной функции играет важную роль во многих областях науки и техники, таких как математика, физика, экономика и т.д. Он позволяет решать различные задачи, такие как нахождение корней уравнений, решение систем уравнений, аппроксимация графиков функций и многое другое.
Однако, не для всех функций существует обратная функция. Для того чтобы функция имела обратную, она должна быть инъективной, то есть каждому значению y должно соответствовать только одно значение x. Для поиска обратной функции существуют различные алгоритмы и методы, которые позволяют ее находить.
Понятие обратной функции
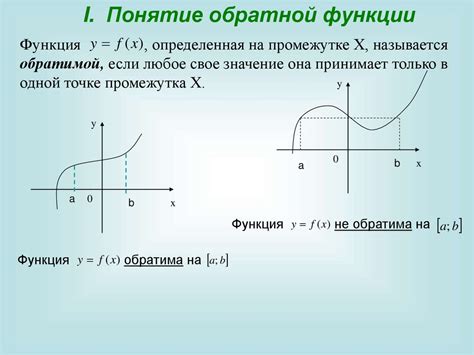
Обратная функция выполняет обратный процесс к исходной функции. Она принимает на вход результат работы исходной функции и возвращает исходное значение. Другими словами, если значение x было преобразовано с помощью функции f(x) в значение y, то обратная функция f^(-1)(y) вернет нам обратно значение x.
Для того чтобы функция имела обратную функцию, она должна быть "однозначной". Это значит, что каждому значению x должно соответствовать только одно значение y. Если функция имеет несколько значений y для одного значения x, то она называется "многозначной" и не имеет обратной функции.
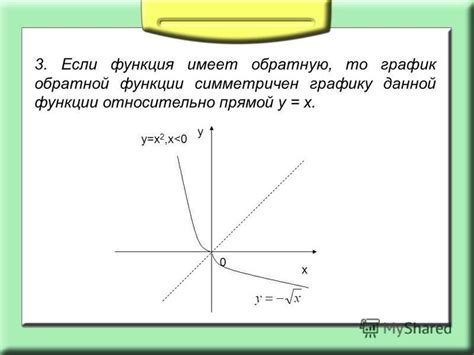
Обратная функция может быть представлена в виде графика, который является зеркальным отражением графика исходной функции относительно прямой y = x. То есть, если точка (x, y) принадлежит графику функции f(x), то точка (y, x) будет принадлежать графику обратной функции f^(-1)(x).
Понятие обратной функции имеет большое значение в различных областях математики и ее применениях. Например, в теории вероятности, при решении уравнений и систем уравнений, а также в алгоритмах и программировании.
Значение обратной функции
Значение обратной функции может быть полезно при решении различных задач, включая системы уравнений, криптографию, оптимизацию и машинное обучение. Обратные функции также находят широкое применение в математическом анализе, алгебре и других областях науки.
Для нахождения значения обратной функции можно использовать различные методы, включая численные методы, алгоритмы и графическое представление. Некоторые функции имеют аналитическое выражение для обратной функции, что упрощает их вычисление. Другие функции могут требовать численного решения или использования специальных алгоритмов.
Значение обратной функции может быть представлено в виде таблицы, графика или математической формулы, в зависимости от конкретной задачи и предпочтений исследователя.
| Функция | Обратная функция |
|---|---|
| y = f(x) | x = f-1(y) |
Значение обратной функции имеет важное значение в практических задачах и науке, так как позволяет решать уравнения, находить обратные зависимости и анализировать функции и их свойства. Важно помнить, что обратная функция может быть определена только для функций, обладающих свойством обратимости.
Определение обратной функции
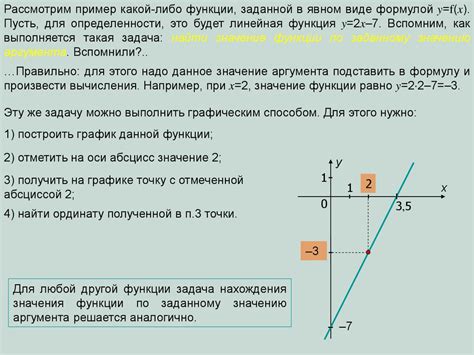
Чтобы определить обратную функцию, необходимо убедиться, что первоначальная функция является биекцией, то есть каждому значению аргумента соответствует только одно значение противоположной функции, и наоборот. Если функция не является биекцией, то она не имеет обратной функции.
Чтобы найти обратную функцию, нужно решить уравнение, в котором неизвестным является аргумент обратной функции. Иногда это можно сделать аналитически, выполнив обратные операции, или путем использования итерационных методов.
Обратные функции играют важную роль в математике и ее приложениях, таких как криптография и статистика. Они позволяют решать уравнения, находить корни и находить обратные преобразования для различных операций. Поэтому понимание обратных функций является ключевым для решения сложных математических задач и создания эффективных алгоритмов.
Примеры

Давайте рассмотрим несколько примеров поиска обратной функции.
Пример 1:
Пусть у нас есть функция f(x) = x^2. Чтобы найти обратную функцию, необходимо решить уравнение y = x^2 относительно x.
Решение:
Исходное уравнение: y = x^2
Выразим x через y: x = sqrt(y) (где sqrt - квадратный корень)
Таким образом, обратная функция будет f^(-1)(y) = sqrt(y)
Пример 2:
Рассмотрим функцию f(x) = 2x + 3. Чтобы найти обратную функцию, необходимо решить уравнение y = 2x + 3 относительно x.
Решение:
Исходное уравнение: y = 2x + 3
Выразим x через y: x = (y - 3) / 2
Таким образом, обратная функция будет f^(-1)(y) = (y - 3) / 2
Пример 3:
Пусть у нас есть функция f(x) = e^x. Чтобы найти обратную функцию, необходимо решить уравнение y = e^x относительно x.
Решение:
Исходное уравнение: y = e^x
Выразим x через y: x = ln(y) (где ln - натуральный логарифм)
Таким образом, обратная функция будет f^(-1)(y) = ln(y)
Это лишь некоторые примеры поиска обратной функции. Надеюсь, что они помогут вам в изучении этой темы.
Пример 1: Обратная функция квадратного корня
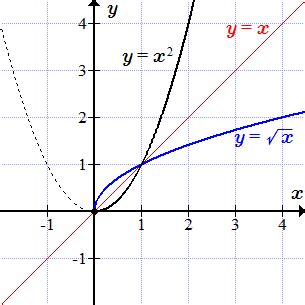
Рассмотрим пример:
Предположим, у нас есть функция f(x) = x2. Чтобы найти обратную функцию, нам нужно решить уравнение f-1(x) = √x.
| Значение x | Значение f(x) = x2 | Значение f-1(x) = √x |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 4 | 16 | 4 |
| 9 | 81 | 9 |
Мы видим, что значения функции и ее обратной функции совпадают для определенных значений x. Однако, обратная функция определена только для неотрицательных значений x, так как квадратный корень может быть только положительным числом или нулем.
Таким образом, обратная функция квадратного корня задается следующим образом:
f-1(x) = √x, где x ≥ 0
Обратная функция позволяет найти исходное значение при заданном результате квадратного корня. Например, если мы знаем, что f-1(x) = 9, то мы можем найти, что x = 81.
Пример 2: Обратная функция логарифма
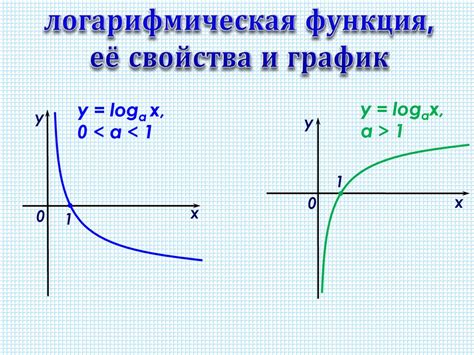
Для нахождения обратной функции логарифма используется основная формула:
Если задано число y и база логарифма b, то обратная функция логарифма может быть найдена следующим образом:
| Обратная функция логарифма: | x = by |
Где x - число, для которого находится обратная функция логарифма, b - база логарифма, а y - результат логарифма.
Например, если имеется логарифм числа 1000 по основанию 10, обратная функция логарифма будет иметь вид:
| Обратная функция логарифма: | x = 103 |
Обратная функция логарифма 1000 по основанию 10 равна 1000.
Пример 3: Обратная функция синуса
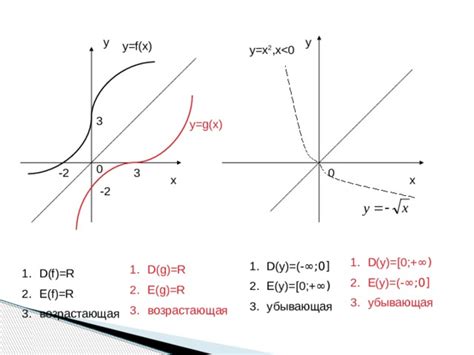
Для нахождения обратной функции синуса можно использовать следующий алгоритм:
- Проверить, что значение x находится в пределах от -1 до 1, поскольку синус определен только в этом диапазоне.
- Использовать формулу arсsin(x) = arcsin(x) = 2 * atan(x / (sqrt(1 - x^2) + 1)).
- Вычислить значение arсsin(x) и вернуть его в качестве результата.
Например, если нам нужно найти обратную функцию синуса для значения x = 0.5, мы можем применить алгоритм:
- Значение x = 0.5 находится в пределах от -1 до 1, поэтому проходим эту проверку.
- Используем формулу arсsin(x) = arcsin(0.5) = 2 * atan(0.5 / (sqrt(1 - 0.5^2) + 1)).
- Вычисляем значение arсsin(0.5) и получаем результат примерно равный 0.5235988 радиан или около 30 градусов.
Таким образом, обратная функция синуса для значения x = 0.5 равна примерно 30 градусам.
Алгоритмы
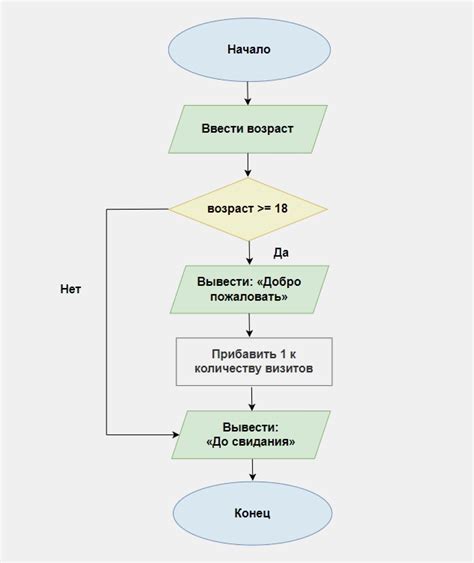
Для нахождения обратной функции существуют различные алгоритмы, которые позволяют найти обратную функцию к заданной функции.
Один из таких алгоритмов - метод замены переменных. Для этого необходимо решить уравнение относительно искомой переменной, а затем выразить ее через известные переменные. Например, если задана функция f(x) = x^2, чтобы найти обратную функцию, мы решаем уравнение f(x) = y относительно x:
x^2 = y
Далее, извлекаем корень из выражения:
x = sqrt(y)
Таким образом, обратная функция к f(x) = x^2 будет f-1(x) = sqrt(x).
Еще одним алгоритмом является метод модуля функции. Для этого сначала решаем уравнение f(x) = y, затем смотрим на возможные значения x относительно модуля функции |f(x)|. Например, если задана функция f(x) = |x|, чтобы найти обратную функцию, мы решаем уравнение f(x) = y:
|x| = y
Затем рассматриваем два случая, в зависимости от значения y:
1. Если y ≥ 0, то x = y.
2. Если y < 0, то x = -y.
Таким образом, обратная функция к f(x) = |x| будет f-1(x) = x при x ≥ 0 и f-1(x) = -x при x < 0.
Это лишь некоторые из алгоритмов, которые могут использоваться для нахождения обратной функции к заданной функции. В каждом конкретном случае может потребоваться применение различных методов и алгоритмов в зависимости от сложности исходной функции.
Алгоритм нахождения обратной функции

Для нахождения обратной функции необходимо выполнить следующий алгоритм:
- Дана функция f(x), для которой требуется найти обратную функцию.
- Решить уравнение y = f(x) относительно x, чтобы выразить x через y.
- Записать полученное выражение в виде функции x = g(y), которая и будет являться обратной функцией.
Таким образом, обратная функция g(y) позволяет найти аргумент x для заданного значения функции y.
Пример:
Дана функция f(x) = 3x - 2.
Для нахождения обратной функции:
- Решим уравнение y = 3x - 2 относительно x:
x = (y + 2) / 3.
- Запишем полученное выражение в виде функции x = g(y) = (y + 2) / 3.
Таким образом, обратная функция к f(x) будет g(y) = (y + 2) / 3.
Алгоритм нахождения обратной функции позволяет получить функцию, обратную к заданной, и использовать её для нахождения исходных аргументов при известных значениях функции.