Плоскость - это геометрическая фигура, которая не имеет толщины и состоит из бесконечного количества точек. Плоскость можно задать с помощью уравнения плоскости, которое позволяет определить все точки этой плоскости.
Если нам дано три точки в трехмерном пространстве, то задача состоит в том, чтобы найти уравнение плоскости, проходящей через эти точки. Уравнение такой плоскости называется общим уравнением плоскости.
Для того чтобы найти общее уравнение плоскости, необходимо использовать уравнение плоскости, которое определяется точностью построения как векторным, так и координатным способами. В результате получается уравнение, которое содержит координаты точек и нормаль плоскости.
Что такое общее уравнение плоскости?

Общее уравнение плоскости имеет следующий вид:
Ax + By + Cz + D = 0
Здесь A, B и C - коэффициенты, которые задают нормальный вектор к плоскости, а D - свободный член.
Нормальный вектор плоскости является перпендикуляром к плоскости и имеет координаты (A, B, C). Он определяет направление, в котором отклоняются все векторы, параллельные плоскости.
Свободный член D определяет расстояние плоскости от начала координат. Для точек, лежащих на плоскости, значение левой части уравнения будет равно 0.
Общее уравнение плоскости позволяет легко определить, принадлежит ли точка плоскости или находится вне ее. Для этого достаточно подставить координаты точки в уравнение и проверить, равно ли значение левой части 0.
Если известны координаты трех точек, принадлежащих плоскости, можно найти коэффициенты уравнения с помощью метода решения системы уравнений.
Общее уравнение плоскости является важным инструментом в геометрии и применяется для решения различных задач, связанных с плоскостью.
Первый шаг в поиске общего уравнения плоскости

Допустим, имеется три точки A(x1, y1, z1), B(x2, y2, z2) и C(x3, y3, z3). Чтобы найти вектор AB, необходимо вычислить разности координат:
| Вектор | Формула |
|---|---|
| AB | AB = B - A = (x2 - x1, y2 - y1, z2 - z1) |
| AC | AC = C - A = (x3 - x1, y3 - y1, z3 - z1) |
Получив векторы AB и AC, можно рассчитать их векторное произведение, чтобы получить вектор, перпендикулярный плоскости, проходящей через эти точки. Векторное произведение можно вычислить по следующей формуле:
| Векторное произведение | Формула |
|---|---|
| AB x AC | (y2 - y1)(z3 - z1) - (z2 - z1)(y3 - y1), (z2 - z1)(x3 - x1) - (x2 - x1)(z3 - z1), (x2 - x1)(y3 - y1) - (y2 - y1)(x3 - x1) |
Полученный вектор будет нормалью плоскости, проходящей через заданные точки. Зная нормаль и координаты одной из точек, можно записать общее уравнение плоскости.
Как найти векторы, лежащие в плоскости?

- Выберите две из трёх заданных точек и обозначьте их координатами (x1, y1, z1) и (x2, y2, z2).
- Постройте вектор, соединяющий эти две точки, используя разность их координат: (x2 - x1, y2 - y1, z2 - z1).
- Вычислите кросс-произведение полученного вектора и вектора, который получен при подстановке координат третьей точки вместо первой точки: результатом будет вектор, лежащий в плоскости.
Графически, векторы, лежащие в плоскости, можно представить как векторы, проведённые в плоскости, параллельные другим векторам, лежащим в этой же плоскости.
Важно помнить, что для определения плоскости по трем точкам необходимо использовать не только векторы, лежащие в плоскости, но и векторное уравнение. Это уравнение может быть записано следующим образом:
A * (x - x1) + B * (y - y1) + C * (z - z1) = 0
Здесь A, B и C - компоненты вектора, лежащего в плоскости. (x, y, z) - переменные координаты точки на плоскости, а (x1, y1, z1) - координаты одной из заданных точек. Осталось найти значения A, B, C, используя кросс-произведение описанные выше шаги.
Второй шаг в поиске общего уравнения плоскости
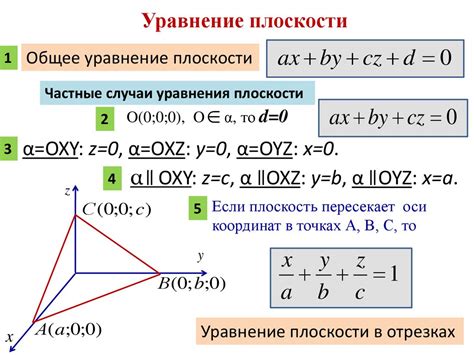
Для нахождения вектора нормали можем воспользоваться известной формулой для определения нормали координатного уравнения плоскости: Ax + By + Cz + D = 0. В этой формуле коэффициенты A, B, C отвечают за направление вектора нормали, а также за наклон плоскости к осям координат. Для определения этих коэффициентов используем координаты найденных точек и заменим их в формулу.
После подстановки получим систему уравнений относительно коэффициентов A, B, C и D. Решив эту систему, найдем значения данных коэффициентов и сможем описать плоскость с помощью общего уравнения.
Вектор нормали имеет важное физическое значение и используется в различных областях науки и техники. Он указывает на направление прямой, перпендикулярной к плоскости, и может быть полезен при решении различных геометрических задач.
Как составить систему уравнений плоскости по 3 точкам?

Для составления системы уравнений плоскости, проходящей через три заданные точки, необходимо использовать уравнение плоскости в общем виде. Данное уравнение имеет вид:
Аx + Вy + Сz + D = 0,
где (x, y, z) - координаты точки на плоскости, A, B, C - коэффициенты, которые определяют нормальный вектор плоскости, а D - свободный член.
Для составления системы уравнений необходимо подставить координаты каждой из трех заданных точек в уравнение плоскости. Полученная система будет представлять собой три уравнения с тремя неизвестными (A, B, C).
Для удобства можно представить систему уравнений в виде таблицы:
| Точка | x | y | z | Уравнение |
|---|---|---|---|---|
| Точка 1 | x1 | y1 | z1 | Ax1 + By1 + Cz1 + D = 0 |
| Точка 2 | x2 | y2 | z2 | Ax2 + By2 + Cz2 + D = 0 |
| Точка 3 | x3 | y3 | z3 | Ax3 + By3 + Cz3 + D = 0 |
Затем необходимо решить данную систему уравнений относительно неизвестных A, B, C, D. Решение системы позволит найти общее уравнение плоскости, проходящей через заданные точки.
Таким образом, составив систему уравнений плоскости по трем точкам и решив ее, можно найти общее уравнение плоскости, используя которое можно определить, принадлежит ли точка плоскости или нет, а также проводить другие необходимые вычисления и рассуждения.
Третий шаг в поиске общего уравнения плоскости

После того, как мы нашли нормальный вектор плоскости, третий шаг заключается в записи уравнения плоскости в общей форме.
Общее уравнение плоскости имеет вид:
Ax + By + Cz + D = 0,
где A, B, C - коэффициенты, определенные нормальным вектором плоскости, а D - полученное значение.
Для определения значений A, B, C и D, мы используем координаты одной из точек, через которые проходит плоскость. Подставив в уравнение плоскости значения координат этой точки, мы можем вычислить D.
Таким образом, третий шаг включает в себя запись уравнения плоскости в общей форме, с использованием полученных коэффициентов и вычисленного значения D.
Как найти нормаль к плоскости и записать общее уравнение?

Для начала, найдем векторы, соединяющие точки на плоскости. Затем, используя эти векторы, найдем два вектора, лежащих на плоскости. Вычислим их векторное произведение, чтобы найти нормаль к плоскости.
Когда нормаль к плоскости найдена, можно записать общее уравнение плоскости в виде Ax + By + Cz + D = 0, где (A, B, C) – координаты нормального вектора, а (x, y, z) – координаты любой точки на плоскости.
Процесс нахождения нормали и записи общего уравнения прост и понятен. Зная эти шаги, вы можете легко найти нормаль к любой плоскости и записать ее общее уравнение.
Для наглядности приведена таблица с пошаговым алгоритмом:
| Шаг | Действие |
|---|---|
| 1 | Найти векторы, соединяющие три точки на плоскости |
| 2 | Используя найденные векторы, найти два вектора, лежащих на плоскости |
| 3 | Вычислить векторное произведение найденных векторов, чтобы найти нормаль к плоскости |
| 4 | Записать общее уравнение плоскости в виде Ax + By + Cz + D = 0, используя координаты нормального вектора |