Огибающая семейства кривых – это важный объект изучения в математике, который позволяет изучать поведение множества кривых в определенном семействе. Нахождение огибающей может быть полезным при решении различных задач и поиске оптимальных решений. В данной статье мы рассмотрим несколько методов и советов, которые помогут вам найти огибающую семейства кривых.
Важным шагом в поиске огибающей семейства кривых является определение уравнения семейства искомых кривых. Для этого необходимо проанализировать параметры, определяющие кривые в семействе, и найти их аналитическую зависимость друг от друга. Также полезно определить, какие значения параметров могут принимать, чтобы избежать ложных решений или недопустимых зон значений.
После определения уравнения семейства кривых можно приступить к поиску огибающей. Для этого необходимо найти условие, которому должно удовлетворять каждая кривая в семействе, чтобы она являлась огибающей. Обычно это условие выражается в виде системы уравнений или дифференциального уравнения, зависящего от параметров семейства. Решив это уравнение, можно получить уравнение огибающей семейства кривых.
Рассмотрение геометрического определения огибающей кривой
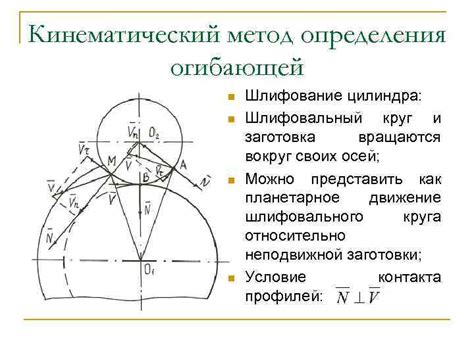
Для построения огибающей кривой можно использовать следующий алгоритм:
- Выбрать некоторую точку на плоскости.
- Провести касательную к каждой кривой семейства в этой точке.
- Найти точку пересечения всех касательных.
- Повторить шаги 1-3 для разных точек на плоскости.
- Полученные точки пересечения являются точками огибающей кривой.
Таким образом, используя геометрическое определение огибающей кривой, можно найти ее графическое представление и увидеть особенности семейства кривых.
Использование аналитических методов для нахождения огибающей семейства

Аналитические методы играют важную роль в нахождении огибающей семейства кривых. Они позволяют нам математически описать кривые и найти их общие свойства. С помощью аналитических методов мы можем определить уравнение огибающей семейства и найти ее геометрическую форму.
Одним из основных аналитических методов является решение дифференциального уравнения, которое описывает данное семейство кривых. Решая это уравнение, мы найдем уравнение огибающей семейства. Для этого используются различные методы решения дифференциальных уравнений, такие как метод разделения переменных, метод вариации постоянной и метод Лагранжа.
Еще одним полезным аналитическим методом является построение параметрических уравнений для кривых семейства. Параметрическое уравнение состоит из двух функций, которые описывают координаты точек на кривой в зависимости от параметра. Используя параметрические уравнения, мы можем наглядно представить огибающую семейства и производить различные геометрические операции с ней.
Кроме того, аналитические методы позволяют нам найти особые точки на огибающей семействе, такие как экстремумы и точки перегиба. Это очень полезная информация, которая помогает нам понять структуру и поведение кривых в семействе.
Таким образом, использование аналитических методов для нахождения огибающей семейства кривых позволяет нам получить более глубокое представление о ее свойствах и структуре. Эти методы не только помогают нам математически описать кривые, но и дают нам возможность провести различные геометрические исследования.
Применение математических вычислений и теории вероятности

Применение математических вычислений и теории вероятности играет важную роль при нахождении огибающей семейства кривых. Эти методы позволяют анализировать данные, определить зависимости и предсказывать результаты.
Математические вычисления позволяют решать сложные задачи, основанные на алгоритмах и формулах. Они позволяют нам определить точное распределение кривых в пространстве и найти решения в трудных случаях.
Теория вероятности позволяет оценивать вероятность того, что некоторое событие произойдет или не произойдет. Она основана на определении вероятности как отношения числа благоприятных исходов к общему числу возможных исходов. В контексте огибающей семейства кривых, теория вероятности может помочь определить насколько вероятно нахождение кривой в определенной точке.
Применение математических вычислений и теории вероятности в нахождении огибающей семейства кривых позволяет улучшить точность и надежность результатов. Эти методы помогают предсказывать будущие значения, анализировать зависимости и устанавливать связи между различными переменными.
Важно отметить, что для применения математических вычислений и теории вероятности при поиске огибающей семейства кривых необходимо иметь соответствующие навыки и знания. Необходимо быть знакомым с основными понятиями и методами математики и обладать умением использовать их в практических задачах.
Роль компьютерных программ и алгоритмов в поиске огибающей семейства кривых

В современной науке и технологиях роль компьютерных программ и алгоритмов в поиске огибающей семейства кривых становится все более значительной и важной. Компьютерные программы позволяют сократить время и усилия, затрачиваемые на поиск огибающей, и обеспечивают более точные и эффективные результаты.
Одним из основных применений компьютерных программ и алгоритмов в поиске огибающей семейства кривых является автоматизация процесса анализа данных и вычислений. С использованием специализированных программ и алгоритмов можно быстро обрабатывать большие объемы данных, проводить сложные математические вычисления и графические представления результатов.
Программы и алгоритмы, разработанные специально для поиска огибающей семейства кривых, обеспечивают возможность нахождения оптимальной огибающей, которая наилучшим образом аппроксимирует ряд кривых. Это особенно полезно в задачах обработки и анализа временных рядов, когда необходимо выделить основную тенденцию и убрать шумы и артефакты.
С помощью компьютерных программ и алгоритмов можно также проводить визуализацию результатов поиска огибающей. Это позволяет исследователям и аналитикам наглядно представлять и анализировать полученные данные, что делает процесс их интерпретации более простым и понятным.
Благодаря развитию технологий и возможностей компьютерных программ и алгоритмов в поиске огибающей семейства кривых становится все более доступным и эффективным. Они позволяют исследователям и специалистам в разных областях науки и техники получать более точные и надежные результаты, а также сокращать время и ресурсы, затрачиваемые на проведение анализов и вычислений.
В итоге, использование компьютерных программ и алгоритмов в поиске огибающей семейства кривых является неотъемлемой частью современной науки и технологий, обеспечивая более точные, эффективные и наглядные результаты и упрощая процесс исследования и анализа данных.
Практические примеры и применение огибающих семейств кривых в различных областях

Огибающие семейства кривых находят широкое применение в различных областях: от математики и физики до компьютерной графики и дизайна. Ниже представлены несколько практических примеров использования огибающих семейств кривых.
1. Математика:
В математике огибающие семейства кривых используются для моделирования различных геометрических объектов и фигур. Например, огибающие семейства эллипсов и гипербол используются для описания орбит планет и спутников, а огибающие семейства кривых Безье используются в компьютерной графике для создания плавных кривых и поверхностей.
2. Физика:
В физике огибающие семейства кривых используются для описания движения и траектории различных тел и частиц. Например, огибающие семейства параболических кривых применяются для моделирования полёта снарядов и ракет, а огибающие семейства синусоид используются для описания колебаний и волн.
3. Дизайн:
В дизайне огибающие семейства кривых могут быть использованы для создания интересных и эстетически привлекательных композиций. Например, огибающие семейства спиралей и синусоид могут использоваться в оформлении логотипов, украшении упаковки и декоративных элементов.
4. Архитектура:
В архитектуре огибающие семейства кривых используются для создания изящных и гармоничных форм. Например, огибающие семейства парабол, эллипсов и гипербол могут использоваться для моделирования арок, сводов и куполов в зданиях и сооружениях.
5. Биология:
В биологии огибающие семейства кривых используются для моделирования форм и структур живых организмов. Например, огибающие семейства спиралей применяются для описания спирали ДНК, а огибающие семейства кривых Безье используются для моделирования формы листьев и путей распространения нервных импульсов.
Таким образом, огибающие семейства кривых имеют широкий спектр применения и находят применение в различных областях, помогая создавать красивые и функциональные объекты и структуры.