Как найти ось функции по уравнению — подробное руководство для начинающих

При изучении математики, особенно алгебры и геометрии, важно знать, как найти ось функции по уравнению. Ось функции играет важную роль в определении ее характеристик и поведения. Поэтому, разбираясь с уравнениями, мы должны уметь определить ось симметрии заданной функции.

Ось симметрии функции - это такая вертикальная линия, которая разделяет график функции на две симметричные части. Эта линия обладает тем свойством, что любая точка с графика функции, находящаяся относительно нее на одинаковом расстоянии, будет иметь одинаковые значения. Таким образом, ось симметрии функции может служить точкой отсчета и обеспечивать симметричность значений функции относительно нее.

Для определения оси симметрии функции по ее уравнению необходимо провести анализ выражения функции и учесть некоторые особенности. Существуют разные типы функций, и каждый тип имеет свои специфические характеристики и методы определения оси симметрии. Например, уравнение квадратной функции имеет вид y = ax^2 + bx + c, где a, b и c - это коэффициенты, а x - переменная. Ось симметрии квадратной функции всегда проходит через вершину графика, которая имеет координаты (-b/(2a), f(-b/(2a))), где f(x) - заданная функция.

Разбор уравнения: порядок действий и методы решения

1. Изучение типа уравнения: начните с определения типа уравнения, с которым вы работаете. Это может быть линейное уравнение, квадратное уравнение, тригонометрическое уравнение и т. д. Каждый тип уравнения требует своего подхода к решению.
2. Приведение уравнения к стандартному виду: следующий шаг – привести уравнение к стандартному виду, чтобы упростить его решение. Для этого может потребоваться применение алгебраических преобразований, факторизации и других методов.
3. Применение методов решения: когда уравнение приведено к стандартному виду, можно использовать методы решения. Например, для линейных уравнений применяется метод Крамера, для квадратных уравнений – дискриминант и так далее. Изучите доступные методы решения уравнения и примените подходящий метод для вашего конкретного случая.
4. Проверка решения: после нахождения корней уравнения, всегда рекомендуется проверить полученные значения, подставив их обратно в исходное уравнение. Это позволяет удостовериться, что найденные значения являются действительными решениями.

Следуя этим шагам и выбирая соответствующие методы решения, вы сможете успешно разобраться с уравнениями различной сложности. Помните, что практика играет важную роль в овладении этим навыком, поэтому не стесняйтесь тренироваться на различных уравнениях.

Оси симметрии и основные понятия

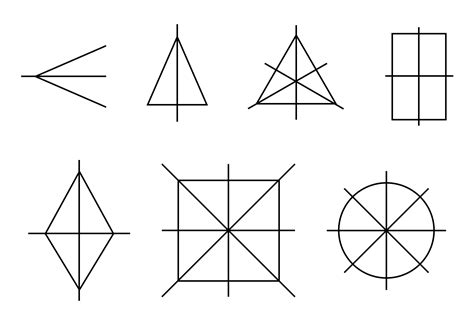
Ось симметрии можно найти, рассмотрев график функции и определив, где он пересекает линию под прямым углом. Например, если график функции представляет собой симметричную фигуру относительно вертикальной линии, то эта линия будет вертикальной осью симметрии функции.

Оси симметрии играют важную роль в анализе функций. Они помогают нам определить основные свойства функции, такие как максимальное и минимальное значение, точки перегиба и другие характеристики. Знание осей симметрии позволяет нам более точно изучать и анализировать функции и предсказывать их поведение.

Важно отметить, что не все функции имеют ось симметрии. Некоторые функции могут быть асимметричными или иметь более сложные формы. Однако понимание основных понятий осей симметрии поможет вам лучше понять и анализировать функции в дальнейшем.

График функции и его свойства

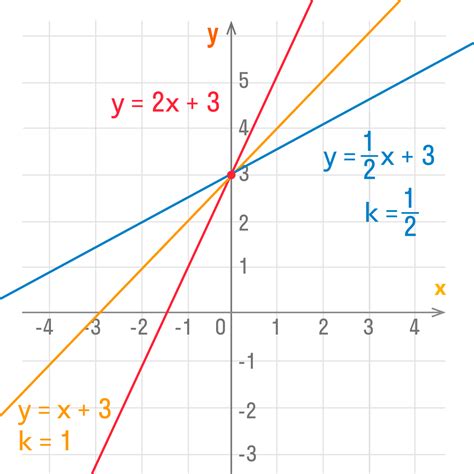
График функции может быть построен по ее уравнению, которое связывает значения аргумента и значения функции. Построение графика функции позволяет определить основные свойства функции, такие как область определения, область значений, монотонность, экстремумы, асимптоты и другие.

На графике функции можно определить ось симметрии – это ось, относительно которой график функции симметричен. Ось симметрии может быть вертикальной или горизонтальной. Также на графике можно определить точку пересечения с осями координат – это точки, в которых график функции пересекает оси координат.

График функции может иметь различные формы: прямые линии, параболы, гиперболы и т.д. Форма графика функции тесно связана с ее уравнением и может давать информацию о поведении функции в различных областях.

Изучение графика функции позволяет получить представление о ее поведении и свойствах, что является важным для анализа функции и решения различных задач в математике и других науках.

Нахождение оси функции по графику

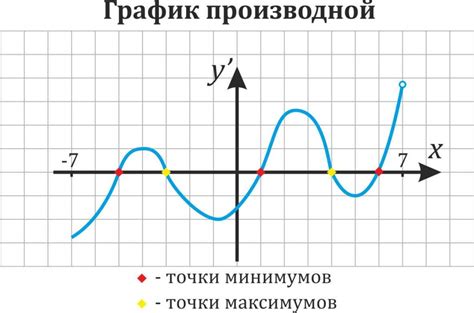
Для нахождения оси функции по графику необходимо проанализировать его симметрию и поведение функции на графике.

• Первым шагом является определение наличия симметрии относительно оси OY. Если график функции является симметричным относительно оси OY, то осью функции будет являться эта ось.
• Если график функции не является симметричным относительно оси OY, то необходимо проанализировать, как график функции ведет себя в окрестности оси OX.

Для этого можно обратить внимание на следующие моменты:

1. Если у функции есть асимптота, то осью функции будет являться линия асимптоты.
2. Если ось функции является линией симметрии кривизны, то она может быть найдена, проанализировав область локального максимума или минимума.
3. Если на графике функции есть точка перегиба, то осью функции может быть прямая, проходящая через эту точку.
4. Если ни одно из вышеперечисленных условий не выполняется, то ось функции может быть определена только графическим путем, посредством сопоставления функции с графиками известных функциональных типов.

В любом случае, для нахождения оси функции по графику требуется внимательное исследование графического представления функции, а также учет особых точек на графике, таких как точки пересечения с осями координат, точки экстремума и точки перегиба.

Оси функции при наличии параметров

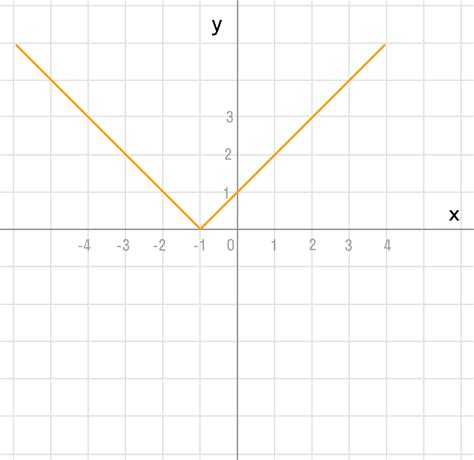
При наличии параметров в уравнении функции, определение оси функции может усложняться. В таком случае, ось функции может зависеть от значений параметров. Например, для функции вида y = ax^2 + bx + c, где a, b, c - параметры, ось функции может быть найдена по формуле x = -b/2a. Значение этой формулы может изменяться в зависимости от значений параметров a и b.

Для понимания, как ось функции зависит от параметров, можно использовать геометрическую интерпретацию. График функции y = ax^2 + bx + c представляет собой параболу, которая может менять свое положение и форму в зависимости от параметров. Осью функции будет являться вертикальная прямая, которая проходит через вершину параболы. Вершина параболы может находиться выше или ниже оси x, а также может быть направлена вверх или вниз в зависимости от параметров.

Чтобы найти ось функции при наличии параметров, следует использовать дополнительные знания о графике функции и его свойствах. Например, для параболы y = ax^2 + bx + c:

• если a > 0, то парабола открывается вверх и ее вершина будет минимумом функции;
• если a
• если b = 0 и a ≠ 0, то парабола симметрична относительно оси y;
• если b ≠ 0 и a = 0, то парабола симметрична относительно вертикальной прямой, проходящей через x = -c/b;
• если a ≠ 0 и b ≠ 0, то парабола симметрична относительно вертикальной прямой, проходящей через x = -b/2a.