Трапеция - это геометрическая фигура, которая имеет две параллельные стороны, называемые основаниями, и две непараллельные стороны, называемые боковыми сторонами. Одной из оснований трапеции может быть известная сторона, а найти нужно длину другого основания. Узнать, как найти основание трапеции через другое основание, можно, используя определенные формулы и свойства этой геометрической фигуры.
Для нахождения длины другого основания трапеции можно использовать свойства параллельных сторон и пропорцию. Общий способ состоит в применении теоремы Пифагора для нахождения длины боковой стороны и параллельности боковых сторон, чтобы найти длину другого основания. Следуя определенному порядку действий и используя эти формулы, вы сможете легко найти основание трапеции через другое основание.
Итак, чтобы найти основание трапеции через другое основание, вам нужно знать длину одного из оснований и других сторон трапеции. Затем примените соответствующие формулы и свойства трапеции, чтобы выразить длину искомого основания через уже известные данные. Это руководство познакомит вас с простыми и эффективными способами нахождения основания трапеции через другое основание.
Основание трапеции: как найти через другое - подробное руководство
Для начала, вспомним основные свойства трапеции. Она имеет две параллельные стороны, называемые основаниями, и две непараллельные равные стороны, называемые боковыми сторонами. Сумма углов трапеции равна 360 градусов.
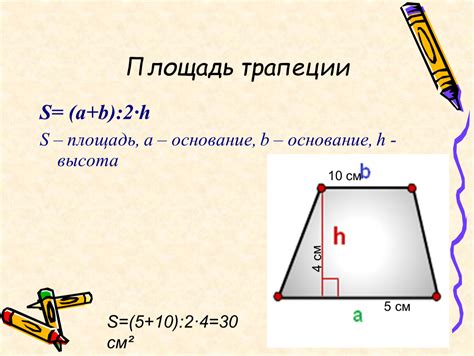
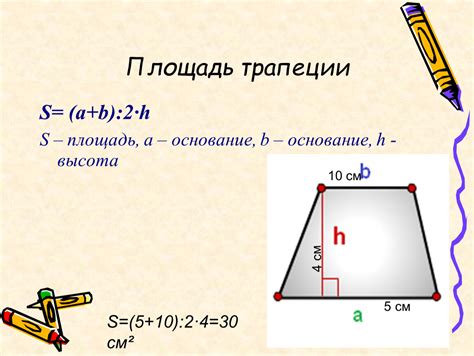
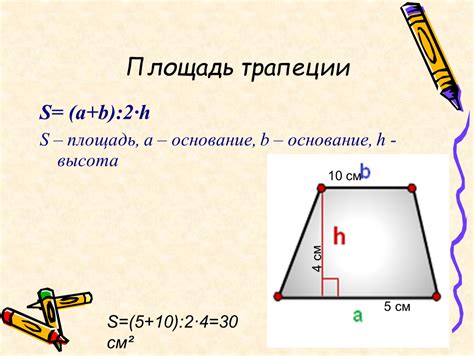
Если мы знаем одно основание трапеции и высоту, мы можем использовать формулу для нахождения площади трапеции: S = (a + b) * h / 2, где a и b - основания трапеции, h - высота. Из этой формулы можно выразить одно основание через другое и высоту: a = (2 * S - b * h) / h, b = (2 * S - a * h) / h.
Если же нам даны длины обоих оснований и высота, то мы можем найти сумму длин боковых сторон трапеции: c = sqrt(a^2 + b^2 - 2 * a * b * cos(alpha)), где c - длина боковой стороны, alpha - угол между основаниями (угол при вершине). Зная сумму длин боковых сторон и длину одного основания, можно найти длину другого основания: a = c - b, b = c - a.
Таким образом, зная одно из оснований трапеции и высоту или зная оба основания и высоту, мы можем определить второе основание. Опираясь на эти знания, можно легко решать задачи по геометрии, требующие нахождения другого основания трапеции.
Не забывайте, что при решении задач всегда стоит внимательно проводить все вычисления и проверять свои ответы. Удачи в изучении геометрии!
Понятие трапеции и ее основания
Основания трапеции - это стороны, которые являются параллельными. Название "основание" пришло от латинского слова "basis", что означает "основа". В трапеции обычно обозначают длину основания большей стороны буквой "a" и длину основания меньшей стороны буквой "b".
Высота трапеции - это перпендикуляр, опущенный из вершины трапеции на основание. Высота обозначается буквой "h".
Зная длины оснований и высоту трапеции, можно найти его площадь по формуле:
S = (a + b) * h / 2,
где S - площадь трапеции, а "2" обозначает деление на два.
Основание трапеции: что это и как оно определяется?
Чтобы найти основание трапеции, первым шагом нужно определить боковые стороны и углы трапеции. Затем, используя формулы для определения площади трапеции или радиуса, можно вычислить длину основания.
Существует несколько способов определения оснований трапеции:
- Если известны длины всех сторон трапеции, можно использовать формулу площади трапеции для определения основания. Формула для площади трапеции: S = ((a + b) * h) / 2, где a и b - длины оснований, h - высота трапеции.
- Если известны длины боковых сторон и углы трапеции, можно использовать теоремы трапеции для определения основания. Например, для прямоугольной трапеции, у которой одно основание является осью симметрии, длина основания может быть найдена с использованием теоремы Пифагора.
- Если известны диагонали и углы трапеции, длина основания может быть найдена с использованием теоремы косинусов. Формула для определения длины основания через диагонали и углы трапеции: a = √(c² + d² - 2cdcos(A)), где a - длина основания, c и d - длины диагоналей, A - угол между диагоналями.
Зная определение основания трапеции и используя соответствующие формулы, можно точно определить и вычислить его длину.
Условие равенства оснований трапеции
Для того чтобы найти основание трапеции через другое основание, необходимо выполнение условия равенства оснований. Условие состоит в том, что противоположные стороны трапеции должны быть параллельны.
Если стороны трапеции параллельны, то можно использовать свойство равенства оснований. Это свойство гласит, что две диагонали трапеции делят ее на две подобные треугольники. В этих треугольниках отношение длин боковых сторон (боковые стороны трапеции) к длинам боковых сторон (боковые стороны равнопропорциональных треугольников) одинаково. Из этого свойства следует, что основания трапеции также будут равными.
Таким образом, для нахождения основания трапеции через другое основание можно проверить, являются ли противоположные стороны трапеции параллельными. Если это условие выполняется, то можно заключить, что основания трапеции равны.
Определение одного основания через другое и другие параметры трапеции
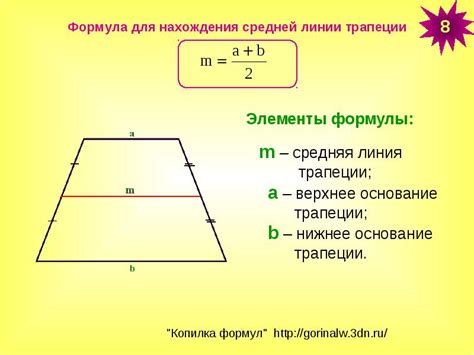
Чтобы определить одно основание трапеции через другое, необходимо использовать свойства параллельных прямых. Рассмотрим трапецию ABCD:
AB и CD – основания трапеции, которые являются параллельными прямыми;
BC и AD – боковые стороны трапеции.
Также для определения длины одного основания через другое и другие параметры трапеции необходимо использовать следующие свойства:
1. Высота трапеции является перпендикуляром, опущенным из одного основания к другому. Обозначается буквой h.
2. Средняя линия трапеции является средним перпендикуляром, опущенным от одного основания к другому. Обозначается буквой m.
3. Диагональ трапеции – отрезок, соединяющий противоположные вершины трапеции. Обозначается буквой d.
Зная значения хотя бы двух параметров – одного из оснований, высоты, средней линии или диагонали можно определить длину другого основания трапеции, используя соответствующие формулы или свойства.
Таким образом, понимание определения одного основания через другое и другие параметры трапеции позволяет более гибко решать геометрические задачи, связанные с этой фигурой, и углубить свои знания в области геометрии.
Формула для поиска основания трапеции через другое основание
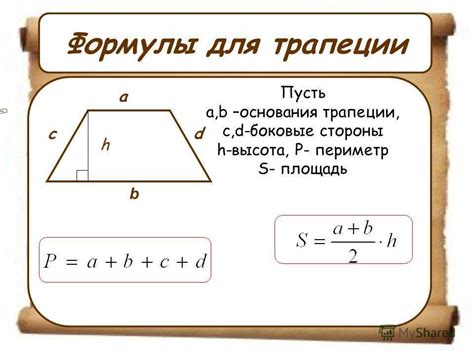
Основание трапеции можно найти, используя формулу для вычисления площади трапеции и известное значение другого основания, высоты и площади.
Пусть a и b - основания трапеции, h - высота, S - площадь.
Формула:
a = 2 * S / (b + h)
Для вычисления основания трапеции через другое основание, нужно знать значение площади и другое основание, а также значени высоты трапеции.
Пример:
Для трапеции с площадью S = 24 и основанием b = 8, найдем основание a.
Известные значения подставим в формулу:
a = 2 * 24 / (8 + h)
Далее, решим полученное уравнение относительно h:
h = 2 * 24 / a - 8
Подставляя a = 2, получаем:
h = 2 * 24 / 2 - 8 = 12 - 8 = 4
Таким образом, найденное значение высоты равно h = 4. Зная это, мы можем найти значение второго основания, подставив известные значения в формулу:
a = 2 * 24 / (8 + 4) = 2 * 24 / 12 = 4
Таким образом, основание a равно 4.
Используя данную формулу, вы сможете легко найти основание трапеции через другое основание, имея известные значения площади и высоты. Это может быть полезно при решении геометрических задач или при работе с фигурами, имеющими форму трапеций.
Примеры решения задач по нахождению основания трапеции
Ниже приведены несколько примеров задач, в которых требуется найти значение основания трапеции.
Пример 1:
Известны длины боковых сторон трапеции - 8 и 12 см, а также диагональ, соединяющая нижние концы оснований - 10 см. Найдите значения оснований трапеции.
Решение:
Обозначим основания трапеции как a и b. Используя теорему Пифагора, найдем значение третьей стороны трапеции:
c = √(a² - b²) = √(10² - (8-12)²) = √(100 - 16) = √84 ≈ 9.17 см
Теперь, зная значение диагонали и одного основания, можем найти второе основание:
c² = a² - b² → b² = a² - c² → b² = 100 - 84 → b = √16 → b = 4 см
Таким образом, значения оснований трапеции равны 4 и 8 см.
Пример 2:
Длина одного основания трапеции равна 6 см, а длина диагонали, соединяющей вершины оснований - 8 см. Найдите длину второго основания.
Решение:
Обозначим длину второго основания как b. Используя теорему Пифагора, найдем значение диагонали между вершинами оснований:
c = √(a² + b²) = √(6² + b²) = 8
Раскрывая скобки и перенося члены с неизвестной влево, получим:
b² = 64 - 36 = 28
Таким образом, длина второго основания равна √28 ≈ 5.29 см.
Пример 3:
Длины оснований трапеции составляют 10 и 6 см. Известно, что высота трапеции равна 4 см. Найдите площадь трапеции.
Решение:
Обозначим длины оснований как a и b, а высоту трапеции как h. Формула для нахождения площади трапеции выглядит следующим образом:
S = ½(a + b) × h
Подставим известные значения и найдем площадь:
S = ½(10 + 6) × 4 = 16 × 4 = 64 см²
Таким образом, площадь данной трапеции равна 64 квадратным сантиметрам.