Трапеция – это четырехугольник, у которого только две противоположные стороны параллельны между собой. Она является одной из самых распространенных геометрических фигур, которая часто встречается в задачах на геометрию. Если известна площадь трапеции, а также высота или угол наклона боковой стороны, то можно определить длину одной из оснований. В этой статье мы рассмотрим подробный гайд о том, как найти основание трапеции через площадь.
Для начала, помните, что площадь трапеции можно найти по формуле S = ((a + b) * h) / 2, где a и b – длины оснований, а h – высота трапеции. Однако, если известна площадь и одно из оснований, можно найти второе основание. Для этого необходимо знать, что площадь трапеции выражается через одно из оснований и высоту по формуле S = (a + b) * h / 2 или через среднее арифметическое оснований по формуле S = (a + b) * h / 2. Обе эти формулы можно преобразовать для нахождения второго основания.
Итак, давайте рассмотрим два способа нахождения основания трапеции через площадь. Первый способ основан на известной длине одного из оснований, а второй способ лежит в использовании среднего арифметического оснований. Отметим, что для обоих способов необходимо знать площадь и высоту трапеции.
Основание трапеции через площадь: подробный гайд
Для начала, вспомним формулу площади трапеции: S = ((a + b) * h) /2, где a и b – длины оснований, а h – высота. Давайте разрешим это уравнение для нахождения одного из оснований.
1. Для этого, удвоим обе части уравнения: 2S = a + b) * h.
2. Затем, разделим обе части уравнения на h: (2S) / h = a + b.
3. И, наконец, вычтем из обеих частей уравнения второе основание b, чтобы найти a: a = (2S / h) - b.
Теперь, когда мы знаем формулу для нахождения одного из оснований, можно найти значение основания, используя значение площади и высоты трапеции. Просто подставьте значения в формулу и выполните необходимые вычисления.
Не забывайте, что значения должны быть выражены в одной и той же системе измерения. Если площадь задана в квадратных единицах, а высота в сантиметрах, то результат будет выражен в такой же системе измерения.
Зная формулу и следуя предложенным шагам, можно без труда найти основание трапеции по значению площади и высоты.
Формула площади трапеции и ее значение

S = (a + b) * h / 2,
где S - площадь трапеции, a и b - длины оснований, h - высота.
Значение площади трапеции выражается в квадратных единицах (например, квадратных метрах, квадратных сантиметрах и т.д.). Формула позволяет получить точное численное значение площади и использовать ее в дальнейших вычислениях или задачах, связанных с трапецией.
Как найти высоту трапеции через площадь

Высота = (2 × площадь) / (сумма оснований)
Давайте рассмотрим пример, чтобы лучше понять, как применять эту формулу.
| Параметр | Значение |
|---|---|
| Площадь | 36 кв. ед. |
| Основание a | 10 ед. |
| Основание b | 6 ед. |
Подставим известные значения в формулу:
Высота = (2 × 36) / (10 + 6) = 72 / 16 = 4.5 ед.
Таким образом, высота данной трапеции равна 4.5 единицы.
Теперь вы знаете, как найти высоту трапеции через площадь. Это полезное знание поможет вам решать различные задачи, связанные с трапециями и их параметрами.
Как найти сумму оснований трапеции через площадь
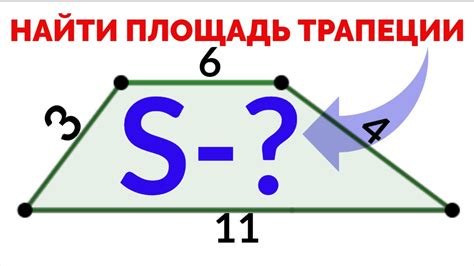
Сумма оснований трапеции может быть найдена, зная ее площадь и высоту. Формула для расчета суммы оснований выглядит следующим образом:
Сумма оснований = (2 * площадь) / высота
Для использования этой формулы необходимо знать значение площади и высоты трапеции. Площадь можно найти, зная длины оснований и высоту, используя формулу:
Площадь = (сумма оснований * высота) / 2
Следует отметить, что формула для расчета суммы оснований работает только при известной площади и высоте. Если иные данные неизвестны, эта формула не применима.
Как найти разность оснований трапеции через площадь
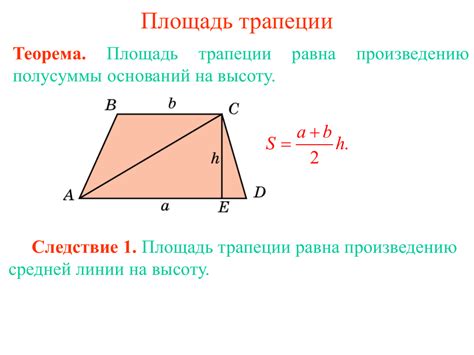
Чтобы найти разность оснований трапеции, сначала нужно выразить одно из оснований через площадь и другое основание. Для этого воспользуемся формулой площади:
S = ((a + b) * h) / 2
Разделим обе части уравнения на h и умножим на 2:
2S/h = a + b
После этого выразим a через b и S:
a = 2S/h - b
Теперь можем выразить разность оснований через площадь:
разность_оснований = a - b = (2S/h - b) - b = 2S/h - 2b = 2(S/h - b)
Таким образом, разность оснований трапеции равна удвоенной разности между площадью трапеции, деленной на высоту, и длиной одного из оснований.
Как найти стороны трапеции через площадь и высоту

Если вам известны площадь и высота трапеции, вы можете найти длины ее оснований с помощью простых математических формул.
Пусть S обозначает площадь трапеции, а h - высоту. Для нахождения оснований a и b воспользуйтесь следующими формулами:
a = 2S / (h + √(h^2 + 8S))
b = 2S / (h - √(h^2 + 8S))
Где √ обозначает квадратный корень, а ^ обозначает возведение в степень.
Используя эти формулы, вы можете легко найти значения оснований трапеции, имея только площадь и высоту. Теперь вы знаете, как найти стороны трапеции через площадь и высоту!
Пример задачи на нахождение основания трапеции через площадь
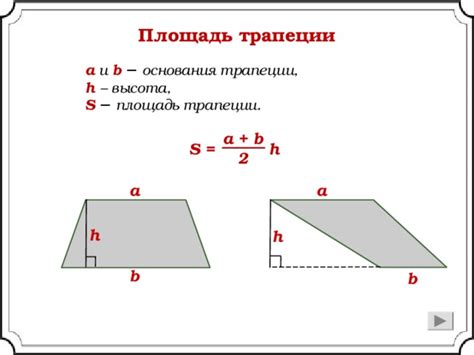
Рассмотрим следующую задачу:
Найдите основание трапеции, если ее площадь равна 24 квадратным сантиметрам, а высота 6 сантиметров.
Для решения данной задачи мы можем использовать формулу площади трапеции:
S = (a + b) * h / 2
где S - площадь трапеции, a и b - основания трапеции, h - высота трапеции.
Подставив известные значения в формулу, получим:
| Формула | Значение |
|---|---|
| 24 = (a + b) * 6 / 2 |
Далее, упростим уравнение:
| Уравнение | Действие | Результат |
|---|---|---|
| 24 = (a + b) * 6 / 2 | Умножение на 2 | 48 = (a + b) * 6 |
| 48 = (a + b) * 6 | Деление на 6 | 8 = a + b |
| 8 = a + b | Вычитание b | 8 - b = a |
Таким образом, мы получили выражение для основания трапеции через площадь и высоту:
a = 8 - b
Для нахождения значения основания a, нужно знать значение основания b. Если значение основания b известно, то подставляем его в выражение и находим значение основания a.
Например, если значение основания b равно 4 сантиметра, то:
a = 8 - 4 = 4 сантиметра
Таким образом, основание трапеции составляет 4 сантиметра.
Полезные советы по нахождению основания трапеции через площадь
Рассчитывая основание трапеции через площадь, следует помнить несколько полезных советов, которые помогут вам выполнить задачу более эффективно:
| 1 | Известна формула для вычисления площади трапеции: S = (a + b) × h / 2, где a и b - основания трапеции, а h - высота. Если известна площадь и высота, можно выразить одно из оснований через другое. |
| 2 | Если известны оба основания трапеции и площадь, можно использовать формулу для нахождения высоты: h = 2 × S / (a + b), где S - площадь, а a и b - основания трапеции. |
| 3 | Если известны только одно основание трапеции и площадь, формула для нахождения второго основания выглядит так: b = 2 × S / (h - a), где S - площадь, h - высота, a - известное основание. |
| 4 | Не забывайте подставлять значения в формулы соответственно и проводить необходимые математические операции. Используйте калькулятор, если это требуется. |
Следуя этим советам, вы сможете найти основание трапеции через площадь с легкостью. Основание трапеции является важным параметром для определения размеров и формы геометрической фигуры, поэтому его нахождение имеет практическое значение при решении различных задач.