Трапеция - это геометрическая фигура, которая имеет две параллельные стороны, называемые основаниями. Зная основания трапеции и её боковые стороны, можно произвести ряд расчетов, включая нахождение площади и периметра. В этой статье мы рассмотрим как найти основание трапеции и выполнить необходимые расчеты по боковым сторонам.

Для начала, рассмотрим как найти основание трапеции. Основания трапеции - это параллельные стороны, поэтому их можно найти зная только одно из них. Допустим, у нас есть одно основание, обозначим его как "a". Также нам известны боковая сторона "b" и высота "h". Чтобы найти второе основание, используем следующую формулу:

a₂ = a₁ + 2b - h

Где "a₂" - второе основание, "a₁" - известное основание, "b" - боковая сторона, "h" - высота трапеции. Подставив известные значения, мы можем найти второе основание. Теперь, когда у нас есть оба основания, мы можем перейти к расчетам по боковым сторонам.

Для расчета площади трапеции, используем следующую формулу:

S = ((a₁ + a₂) * h) / 2

Где "S" - площадь трапеции, "a₁" и "a₂" - основания трапеции, "h" - высота трапеции. Подставив значения оснований и высоты, мы можем вычислить площадь трапеции. Важно помнить, что высота трапеции перпендикулярна основаниям и соединяет их.

Также мы можем произвести расчет периметра трапеции:

P = a₁ + a₂ + b₁ + b₂

Где "P" - периметр трапеции, "a₁" и "a₂" - основания трапеции, "b₁" и "b₂" - боковые стороны трапеции. Сложив значения оснований и боковых сторон, мы получим периметр трапеции.

Теперь вы знаете, как найти основание трапеции и выполнить расчеты по боковым сторонам. Эти формулы помогут вам решать задачи в геометрии и проводить необходимые расчеты трапеций.

Определение и конструкция трапеции

Чтобы построить трапецию, нужно сначала провести две параллельные линии - основания трапеции. Затем, с помощью перпендикуляра, измерить высоту. На основаниях можно отметить точки, которые будут являться вершинами трапеции. После этого, соединив вершины линиями, получится нужная фигура.

Если известны длины боковых сторон трапеции, можно использовать формулы для нахождения основания. Например, если известны боковые стороны a и b, а также длина высоты h, можно использовать следующую формулу для нахождения основания:

1. Основание A = a + 2h / b
2. Основание B = b - 2h / a

Используя эти формулы, можно вычислить значения оснований трапеции и изучить ее свойства и характеристики.

Как найти основание трапеции

• Если известны длины боковых сторон трапеции и ее диагонали, основание можно найти, используя формулу:

a + b = c + d

• Если известны длины оснований трапеции и одного из ее боковых сторон, другое основание можно найти, используя формулу:

a + b = c

• Если известны длины боковых сторон трапеции и угол между ними, основание можно найти, используя теорему синусов:

a + b = 2 * c * sin(угол)

После нахождения основания трапеции, можно провести дальнейшие расчеты, такие как вычисление площади или периметра трапеции.

Как произвести расчеты по боковым сторонам

Для начала, возьмем формулу для вычисления площади трапеции:

Площадь = (сумма оснований * высота) / 2

Пользуясь этой формулой, мы можем найти значение высоты треугольника, а затем использовать ее для расчета боковых сторон.

Теперь, чтобы найти боковую сторону трапеции, нужно воспользоваться теоремой Пифагора. Поскольку мы знаем длину обеих оснований и высоту, мы можем найти длину боковой стороны, используя следующую формулу:

Сторона = √(длина основания1 - длина основания2 + (2 * высота)^2)

Где √ обозначает квадратный корень.

Если мы знаем только длину одного из оснований, высоту и угол между основанием и боковой стороной, мы можем использовать тригонометрию для нахождения длины боковой стороны. Например, если известны длина одного основания, высота и угол α между основанием и боковой стороной, то можно воспользоваться следующей формулой:

Сторона = (длина основания / cos(α))

Где cos(α) обозначает косинус угла α.

Итак, используя эти формулы, вы можете произвести расчеты по боковым сторонам трапеции и получить необходимые значения.

Формула площади трапеции

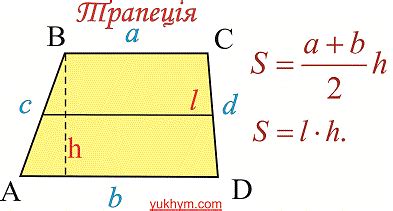
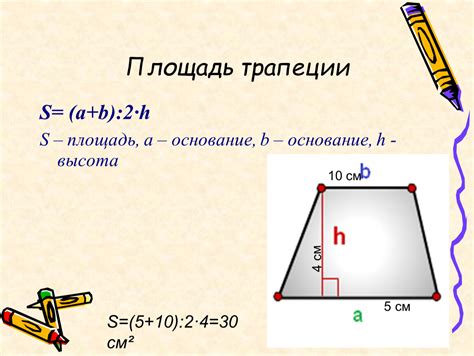
Формула для расчета площади трапеции выглядит следующим образом:

где a и b – длины оснований трапеции, а h – высота трапеции.

Для использования этой формулы необходимо знать значения длин оснований и высоты трапеции.

Применение данной формулы позволяет производить расчеты площади трапеции и использовать ее результаты в дальнейших математических и геометрических задачах.

Применение трапеции в задачах геометрии

Трапеции часто встречаются в геометрических задачах. Они широко используются, например, для нахождения площади фигур или для решения задач на нахождение длин сторон или углов.

Одно из применений трапеции - нахождение площади фигур. Для этого используется формула:

S = (a + b) * h / 2,

где a и b - основания трапеции, а h - высота трапеции.

Также трапеции могут использоваться для нахождения периметра фигур или для нахождения длин сторон, если известны другие стороны и углы.

Трапеции встречаются в различных задачах геометрии и могут быть полезными для решений различных математических задач. Знание основных свойств и формул, связанных с трапециями, помогает эффективнее решать задачи и получать правильные результаты.