Отношение хорды к радиусу – это важный параметр в геометрии, который позволяет определить длину хорды в зависимости от радиуса окружности. Найти это отношение можно с помощью специальной формулы, которая получила название "формула отношения хорды к радиусу". Чтобы легко разобраться в этом вопросе, следуйте данной инструкции.
Для начала, давайте определимся, что такое хорда и радиус в геометрии. Хорда – это отрезок, соединяющий две точки на окружности. Она является одним из основных элементов окружности. Радиус – это отрезок, соединяющий центр окружности с любой точкой на ее границе. Это главная осьметричная линия окружности. Отношение хорды к радиусу показывает, сколько раз длина хорды больше радиуса окружности.
Итак, как найти отношение хорды к радиусу? Для этого вам понадобится использовать следующую формулу: Отношение хорды к радиусу = (2 * длина хорды) / (диаметр окружности). Диаметр окружности – это отрезок, соединяющий две точки на окружности, проходящие через ее центр. Формула отношения хорды к радиусу позволяет найти неизвестное значение, зная лишь длину хорды и радиус окружности.
Изучение отношения хорды к радиусу
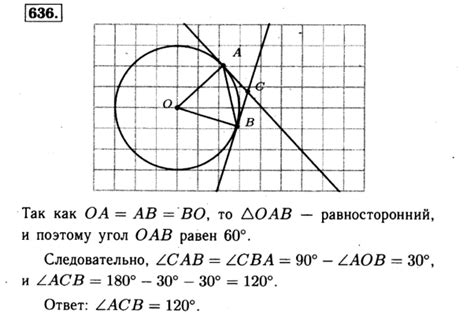
Для вычисления отношения хорды к радиусу используется простая математическая формула:
Отношение хорды к радиусу = (длина хорды) / (длина радиуса)
Это отношение имеет большое значение при изучении геометрии окружностей и применяется во многих математических расчетах. Например, можно использовать отношение хорды к радиусу для нахождения угла между хордой и диаметром окружности или для определения площади сегмента окружности.
Отношение хорды к радиусу также может быть полезным инструментом при построении различных геометрических фигур. Например, для построения правильного пятиугольника можно использовать отношение хорды к радиусу, чтобы определить необходимую длину стороны пятиугольника.
Изучение отношения хорды к радиусу поможет вам лучше понять геометрию окружностей и улучшить свои навыки в решении геометрических задач.
Исследуйте эту важную математическую концепцию и применяйте ее в своих расчетах и построениях!
Значение отношения хорды к радиусу

Формула для вычисления отношения хорды к радиусу выглядит следующим образом:
Отношение хорды к радиусу (ОХ/ОР) = 2sin(α/2)
где ОХ - длина хорды, ОР - длина радиуса, α - центральный угол, выпирающий на данную хорду.
Значение отношения хорды к радиусу может быть как положительным, так и отрицательным. Если значение отношения больше 1, то хорда длиннее радиуса, а если значение меньше 1, то хорда короче радиуса.
Знание значения отношения хорды к радиусу позволяет проводить анализ окружностей и их свойств, а также использовать данный параметр для построения и выполнения различных геометрических задач.
Будьте внимательны при вычислении и использовании данного отношения, чтобы избежать возможных ошибок и получить точные результаты.
Как найти длину хорды:

Формула для вычисления длины хорды выглядит следующим образом:
L = 2 * R * sin(θ/2)
Где L - длина хорды, R - радиус окружности, а θ - центральный угол, опирающийся на данную хорду.
Получить значение центрального угла можно, зная длину хорды и радиус окружности. Для этого используется обратная формула:
θ = 2 * arcsin(L / (2 * R))
Используя эти формулы, можно легко вычислить длину хорды на окружности и использовать эту информацию для решения различных геометрических задач.
Как найти длину радиуса:
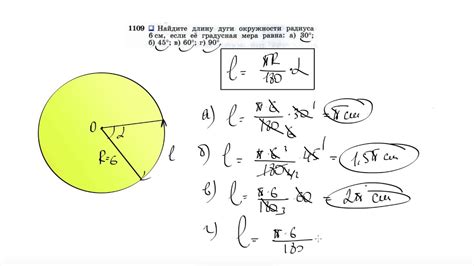
1. Если у вас есть длина окружности, то радиус можно найти по формуле: радиус = длина окружности / (2 * π), где π (пи) приближенно равно 3,14159.
2. Если у вас есть площадь окружности, то радиус можно найти по формуле: радиус = √(площадь окружности / π).
3. Если вы знаете координаты двух точек на окружности, то радиус можно найти с помощью расстояния между этими точками. Для этого нужно найти длину хорды, соединяющей эти точки, а затем разделить ее пополам. Радиус будет являться высотой прямоугольного треугольника, образованного половиной хорды и серединным перпендикуляром к ней.
Независимо от метода вычисления, длина радиуса всегда будет положительным числом, так как в геометрии радиус не может быть отрицательным или равным нулю.
Используйте эти инструкции и формулы, чтобы легко и точно найти длину радиуса в различных задачах и ситуациях.
Инструкция по вычислению отношения хорды к радиусу
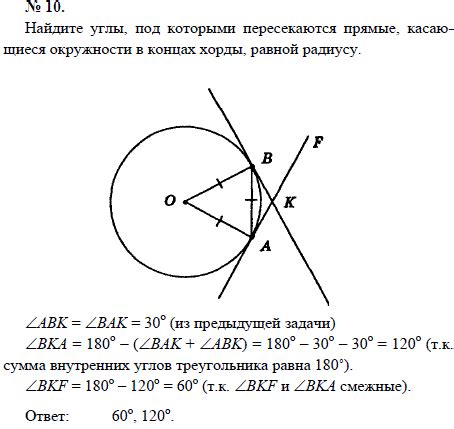
- Выберите окружность, для которой необходимо вычислить отношение хорды к радиусу.
- Измерьте длину хорды с помощью линейки или другого измерительного инструмента. Обозначим это значение как L.
- Измерьте радиус окружности с помощью линейки или другого измерительного инструмента. Обозначим это значение как R.
- Вычислите отношение хорды к радиусу, разделив длину хорды на радиус: отношение = L / R.
- Запишите полученное значение отношения хорды к радиусу.
Отношение хорды к радиусу может быть использовано для решения различных задач в геометрии. Например, оно может быть использовано для нахождения длины хорды или радиуса окружности при известном отношении.
Учтите, что для точности вычислений необходимо иметь достаточно точные измерения длины хорды и радиуса окружности. Приближенные значения могут привести к неточным результатам.
Формула для вычисления отношения хорды к радиусу
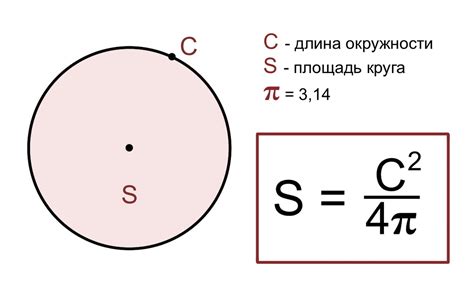
Отношение длины хорды (L) к радиусу окружности (r) можно вычислить с использованием следующей формулы:
L/r = 2sin(θ/2)
Где:
- L - длина хорды
- r - радиус окружности
- θ - центральный угол, образуемый хордой
Эта формула основывается на теореме о центральном угле, которая утверждает, что угол между хордой и радиусом, проведенным к ее концу, в два раза меньше центрального угла, образованного хордой.
Используя эту формулу, вы можете легко вычислить отношение длины хорды к радиусу при известной длине хорды и радиусе окружности. Также вы можете использовать эту формулу для нахождения длины хорды или радиуса, если известно отношение и одна из величин.