Определение отношения между сторонами треугольника по известному углу - одна из ключевых задач в геометрии. Знание этого отношения позволяет решать широкий спектр задач и находить недостающие данные треугольника. На первый взгляд, может показаться сложной задачей найти отношение, однако существуют несколько полезных советов и формул, которые помогут вам справиться с этой задачей.
Сначала следует определить, какие именно данные о треугольнике у вас есть. Если известна длина одной из сторон и значение угла, можно использовать формулу тригонометрии. Для этого используйте теорему синусов или косинусов. Формула синусов определяет отношение синуса угла к противолежащей стороне:
sin(A) = a / c
Где A - заданный угол, a - противолежащая сторона, c - гипотенуза треугольника.
Если же известны две стороны и угол между ними, можно воспользоваться формулой косинусов. Формула косинусов определяет отношение косинуса угла к сторонам треугольника:
cos(A) = (b^2 + c^2 - a^2) / (2 * b * c)
Где A - заданный угол, a, b, c - стороны треугольника.
Используя эти формулы, вы сможете определить отношения между сторонами и углами треугольника, что поможет в решении различных геометрических задач. Помните, что правильное использование формул требует точности и внимания к деталям, поэтому не забывайте проверять свои решения при помощи дополнительных методов и контрольных расчетов.
Формула для нахождения отношения синуса катета к гипотенузе
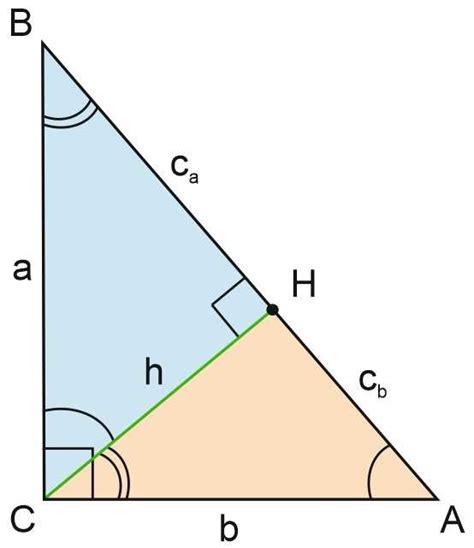
Отношение синуса катета к гипотенузе в прямоугольном треугольнике можно найти с помощью формулы:
sin A = a / c,
где:
- sin A - синус угла A;
- a - длина катета, противолежащего углу A;
- c - длина гипотенузы треугольника.
Данная формула позволяет определить отношение синуса катета и гипотенузы и выразить его в виде десятичной дроби или десятичной записи. Зная значение синуса угла и длину гипотенузы, можно найти длину катета по формуле:
a = sin A * c.
Эта формула является полезной, когда требуется определить длину катета, если известны синус угла и длина гипотенузы. Она часто используется в геометрии, физике и других науках.
Применение косинуса в расчетах треугольника

Применение косинуса наиболее полезно при нахождении длины стороны треугольника, если нам известны длины двух других сторон и значение угла, образованного этими сторонами.
Для расчета длины третьей стороны треугольника можно использовать формулу косинуса:
| cos(α) = (b² + c² - a²) / (2bc) |
Где:
- α – угол, образованный двумя известными сторонами треугольника;
- a, b, c – длины сторон треугольника.
Исходя из этой формулы, мы можем вычислить длину третьей стороны треугольника, зная длины двух других сторон и значение угла, образованного этими сторонами.
Таким образом, применение косинуса оказывается очень полезным при решении задач связанных с треугольниками.
Как найти отношение тангенса катета к гипотенузе
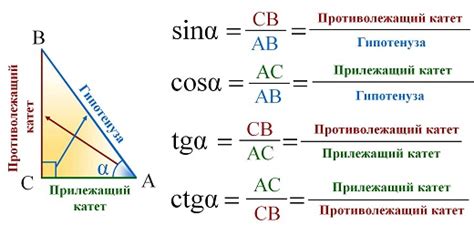
Для того чтобы найти отношение тангенса катета к гипотенузе, необходимо воспользоваться соответствующей формулой:
тангенс угла = длина катета ÷ длина гипотенузы
Эту формулу можно использовать в случае, если известны значения длины катета и гипотенузы треугольника. Зная отношение тангенса катета к гипотенузе, можно определить величину самого угла, используя обратную функцию тангенса.
Важно помнить, что при использовании тангенса необходимо учитывать единицы измерения сторон треугольника. Например, если длина катета и гипотенузы выражены в сантиметрах, то результатом будет тангенс угла в сантиметрах.
Зная отношение тангенса катета к гипотенузе, можно применить эти знания в различных сферах, например, в строительстве, геодезии, физике или компьютерной графике.
Польза котангенса при решении геометрических задач

Основная формула для нахождения котангенса угла может быть записана следующим образом:
cot(α) = cos(α) / sin(α)
где α - угол, для которого мы хотим найти котангенс.
Котангенс часто применяется при решении задач на нахождение неизвестных сторон треугольника или нахождение неизвестного угла, используя известные стороны. Например, если известны длины прилежащего и противолежащего катетов в прямоугольном треугольнике, можно найти котангенс угла между этими катетами. Затем, используя найденное значение котангенса, можно найти значение самого угла при помощи обратной функции - арккотангенса.
Применение котангенса может значительно упростить решение задач и помочь найти нужные значения с использованием уже известных данных. Зная формулу и умея ее применять, можно успешно справляться с задачами, связанными с геометрией и тригонометрией.
Формула для нахождения отношения секанса косинуса к гипотенузе
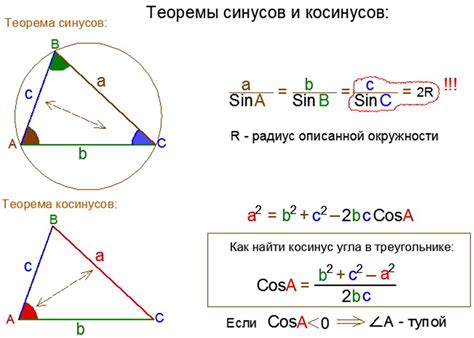
Отношение секанса косинуса к гипотенузе обозначается как secθ / h. Для вычисления этого отношения используется следующая формула:
| secθ | = | 1 / cosθ |
Здесь θ представляет собой значение угла, а cosθ - косинус данного угла. Чтобы найти отношение секанса косинуса к гипотенузе, необходимо сначала найти значение косинуса угла с помощью соответствующей тригонометрической таблицы или калькулятора, а затем подставить его в формулу.
Найдя значение секанса косинуса, можно использовать это отношение для решения различных задач, связанных с треугольниками и тригонометрией.
Возможности мечевидного тангенса
Одним из основных применений мечевидного тангенса является решение задач, связанных с вычислением углов и длин отрезков в треугольниках. При помощи этой функции можно найти отношение угла к стороне треугольника, а также определить неизвестный угол по отношению известных сторон.
Мечевидный тангенс также находит применение в геодезии и навигации. Он помогает определять расстояние между двумя точками на географической карте, а также находить направление от одной точки к другой с помощью компаса.
Другим полезным свойством мечевидного тангенса является его использование в физике для расчетов траекторий движения различных объектов. Например, при помощи этой функции можно определить угол возвышения для достижения заданной дальности полета снаряда или высоты полета дрона.
В целом, мечевидный тангенс – это мощный инструмент, который находит применение в различных областях науки и практической деятельности. Знание его принципов и свойств поможет вам решать сложные задачи и проводить точные измерения.
Применение косеканса в вычислениях

Косеканс часто применяется в вычислениях, связанных с прямоугольными треугольниками и определением отношений сторон и углов. Она может быть полезной для определения длины стороны треугольника, если известны угол и длина другой стороны.
Для вычисления косеканса угла x необходимо взять обратное значение синуса угла: csc(x) = 1/sin(x).
Например, если у вас есть прямоугольный треугольник, в котором известен угол x (например, 30 градусов) и длина стороны a (например, 5 см), вы можете использовать косеканс для определения длины стороны b. По определению косеканса, секущая угла x равна отношению гипотенузы к катету, поэтому b = a * csc(x).
Применение косеканса также может быть полезным для решения задач, связанных с геометрией, физикой или инженерией. Например, при моделировании движения тела под действием силы тяжести или расчете угла наклона поверхности.
Косеканс является одним из фундаментальных элементов тригонометрии и может быть использован для решения различных задач, связанных с вычислениями углов и сторон прямоугольных треугольников.